
- •1.Понятие числовых множеств. Действия над числовыми множествами.
- •2.Числовые промежутки. Окрестность точки.
- •3.Функция.График функции. Способы задания функции.
- •4.Основные характеристики функции: монотонность, четность, периодичность.
- •5.Обратная функция.
- •6.Сложная функция.
- •7.Основные элементарные функции; (степенная, тригонометрические, обратно-тригонометрические, показательная, логарифмическая) их свойства и графики.
- •Корень n-ой степени.
- •Корень n-ой степени, n - четное число.
- •Корень n-ой степени, n - нечетное число.
- •Степенная функция с нечетным положительным показателем.
- •Степенная функция с четным положительным показателем.
- •Степенная функция с нечетным отрицательным показателем.
- •Степенная функция с четным отрицательным показателем.
- •Степенная функция с рациональным или иррациональным показателем, значение которого больше нуля и меньше единицы.
- •Степенная функция с нецелым рациональным или иррациональным показателем, большим единицы.
- •Степенная функция с действительным показателем, который больше минус единицы и меньше нуля.
- •Степенная функция с нецелым действительным показателем, который меньше минус единицы.
- •Показательная функция.
- •Логарифмическая функция.
- •Тригонометрические функции, их свойства и графики.
- •Обратные тригонометрические функции, их свойства и графики.
- •8.Числовые последовательности.
- •Определение
- •Примеры
- •Операции над последовательностями
- •9.Предел числовой последовательности.
- •10.Предельный переход в неравенствах.
- •11.Предел функции в точке.
- •Левый и правый пределы функции
- •13.Предел функции при х→0
- •14.Бесконечно большая функция. Ответ - Бесконечно большая функция
- •15.Определение и основные свойства бесконечно малых функции.
- •16.Связь между функцией, пределом и бесконечно малой величиной.
- •17.Основные теоремы о пределах.
- •Предел монотонной функции
- •19.Первый замечательный предел.
- •Следствия из первого замечательного предела
- •20.Второй замечательный предел(б/д).
- •Следствия из второго замечательного предела
- •21.Сравнение бесконечно малых.
- •22. Основные теоремы о б.М.
- •23.Непрерывность функции в точке и на промежутке.
- •24.Точки разрыва функции и их классификация.
- •25.Основные теоремы о непрерывных функциях.
- •26.Свойства функций, непрерывных на отрезке (б/д). Ответ - Свойства функций непрерывных на отрезке:
- •27.Производная; Ее геометрический и физический смысл.
- •28.Связь между непрерывность. И дифференцируемостью функции.
- •31.Производная обратной функции.
- •32.Производные основных элементарных функций; таблица производных (вывод).
- •33.Дифференцирование неявных функций.
- •34. Дифференцирование параметрический заданных функций.
- •35.Логарифмическое дифференцирование.
- •38.Основные теоремы о дифференциалах.
- •39.Применение дифференциала к приближенным вычислениям.
- •40.Дифференциалы высших порядков. Инвариантность формы dy.
- •41.Теорема Ролля
- •54.Неопределенный интеграл: определение, геометрический смысл.
- •56. Основные свойства интеграла.
- •57. Таблица основных интегралов.
- •58.Интегрирование заменой переменной.
- •59.Интегрирование по частям
- •61.Основыне сведения о разложении многочленов
- •62.Теоремы о разложении рациональной дроби на сумму элементарных дробей
- •63.Основная тригонометрическая подстановка.
Ответы на экзаменационные вопросы по математике
http://vk.com/matan14
1.Понятие числовых множеств. Действия над числовыми множествами.
Ответ - Величиной называется все, что может быть измерено и выражено числом.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множества обозначаются прописными буквами, а элементы множеств строчными буквами. Элементы множеств заключаются в фигурные скобки.
Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).
Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.
Например, перечислением заданы следующие множества:
А={1,2,3,5,7} — множество чисел
Х={x1,x2,...,xn} — множество некоторых элементов x1,x2,...,xn
N={1,2,...,n} — множество натуральных чисел
Z={0,±1,±2,...,±n} — множество целых чисел
Основные числовые множества
|
N |
{1,2,3,...,n} Множество всех натуральных чисел |
|
Z |
{0, ±1, ±2, ±3,...} Множество целых чисел. Множество целых чисел включает в себя множество натуральных. |
|
Q |
Множество рациональных чисел.
Кроме целых чисел
имеются ещё и дроби. Дробь — это
выражение вида Таким образом любое рациональное число можно записать десятичной дробью — конечно или бесконечной периодической. |
|
R |
Множество всех вещественных чисел. Иррациональные числа — это бесконечные непериодические дроби. К ним относятся:
Вместе два множества (рациональных и иррациональных чисел) — образуют множество действительных (или вещественных) чисел. |
Операции над множествами
Пересечение множеств
Пересечением множеств
 и
и называется
множество, обозначаемое
называется
множество, обозначаемое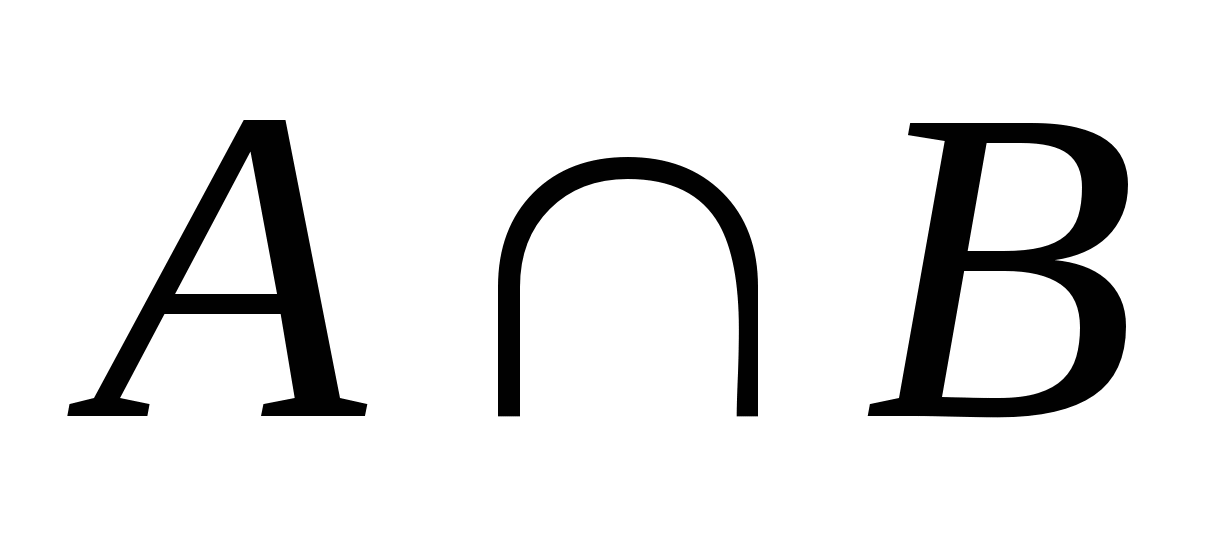 и
состоящее из всех тех и только тех
элементов, которые принадлежат и
множеству
и
состоящее из всех тех и только тех
элементов, которые принадлежат и
множеству ,
и множеству
,
и множеству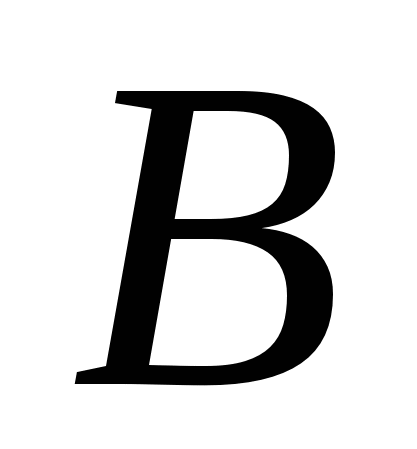 :
:
![]()
 А
А![]() В
В
Объединение множеств
Объединением множеств
 и
и называется
множество
называется
множество ,
состоящее только из тех элементов,
которые принадлежат хотя бы одному из
множеств
,
состоящее только из тех элементов,
которые принадлежат хотя бы одному из
множеств или
или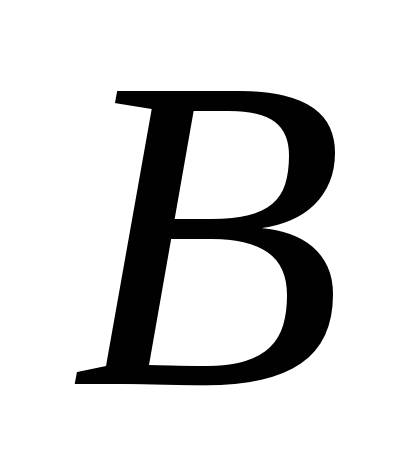 :
:
![]() .
.

 А
А![]() В
В
Рисунок 1.6
Объединение
множеств ![]() содержит
все элементы множества
содержит
все элементы множества![]() и
все элементы множества
и
все элементы множества![]() .
Вычитание
множеств
.
Вычитание
множеств
Разностью между множествами
 и
и называется
множество
называется
множество ,
состоящее из тех элементов множества
,
состоящее из тех элементов множества ,
которые не принадлежат множеству
,
которые не принадлежат множеству ,
то есть
,
то есть .
.
![]()
![]()

![]()
Дополнение
множества
Часто множества ![]() ,
… являются подмножествами некоторого
более широкого множества
,
… являются подмножествами некоторого
более широкого множества![]() ,
принимаемого за универсальное.
,
принимаемого за универсальное.
Для совокупности множеств
 ,
... универсальным множеством называют
каждое множество
,
... универсальным множеством называют
каждое множество такое,
что
такое,
что ,
, ,
, ,
... .
,
... .
Множество
элементов универсального множества ![]() ,
не принадлежащих множеству
,
не принадлежащих множеству![]() ,
называется дополнением множества
,
называется дополнением множества![]() до
множества
до
множества![]() или
просто дополнением и обозначается
или
просто дополнением и обозначается![]() .
Таким образом,
.
Таким образом,![]() .
.

![]()
![]()
![]()
