11 Графические характеристики случайных величин. Гистограмма. Характеристики положения (мода, медиана, выборочная средняя).

Графики вариационных рядов:

1.Полигон частот – при построении графика без интервального вариационного ряда по оси абсцисс откладывают срединные значения классов; по оси ординат – частоты.

Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами (х1р1);(х2р2);…;(хnpn)

2.Гистограмма – интервальный график. При его построении интервального вариационного ряда по оси абсцисс откладывают границы классовых интервалов; по оси ординат – частоты интервалов.

3.Кумулятор – S-образная кривая. По оси абсцисс откладывают значение класса; по оси ординат – накопленные частоты.

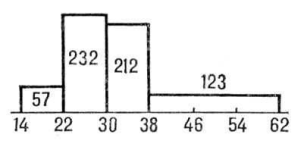
Гистограмма, столбчатая диаграмма, один из видов графического изображения статистического распределении каких-либо величин по количественному признаку. Г. представляет собой совокупность смежных прямоугольников, построенных на прямой линии. Площадь каждого прямоугольника пропорциональна частоте нахождения данной величины в изучаемой совокупности. Пусть, например, измерение диаметров стволов 624 сосен дало следующие результаты:

Диаметр, см-14—22,22—30,30—38,38—62

Число стволов

57,232,212,123

На горизонтальной оси откладываются границы групп, на которые стволы разбиты по их диаметру, и на отрезке, соответствующем каждой группе, строится как на основании прямоугольник с площадью, пропорциональной числу стволов, попавших в данную группу.

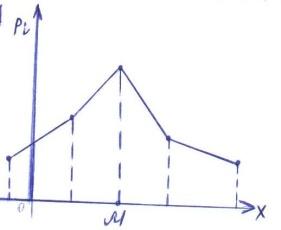
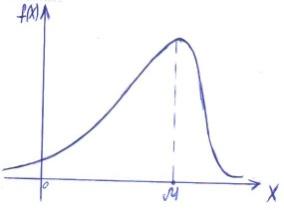
Модой случайной величины называется её наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. На рис. А и Б показана мода соответственно для прерывной и непрерывной случайных величин.

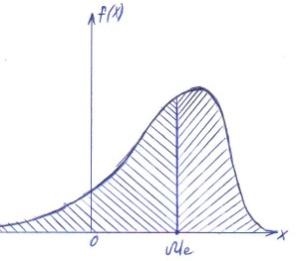
Часто применяется еще одна характеристика положения – так называемая медиана случайной величины. Этой характеристикой пользуются обычно только для непрерывных случайных величин, хотя формально можно её определить и для прерывной величины. Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.Если все значения признака выборки различны, то

Если же все значения имеют частоты n1, n2,…,nk, то

12. Прямые и косвенные измерения погрешности измерений абсолютная и относительная погрешности измерений систематическая приборная грубая случайная погрешности примеры

Прямые измерения проводят с помощью приборов, которые измеряют саму исследуемую величину. Так, массу тел можно найти с помощью весов, длину измерить линейкой, а время - секундомером. Те же величины в других случаях могут быть найдены только с помощью косвенных измерений - пересчетом других величин, значения которых получены в результате прямых измерений. Так находят массу Земли, расстояние от Земли до Солнца, продолжительность геологических периодов.

Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

абсолютная — ΔА; она выражается в единицах измеряемого значения и представляет собой разность между измеренным Ах и действительным А значениями физической величины: ΔА = Ах — А

Относительная погрешность измерения равна δ; она обычно выражается в процентах и представляет собой отношение абсолютной погрешности к действительному значению измеряемой величины:

δ= ΔА / А ≈ = ΔА / Ах ,

δ = 100 ΔА / А.

Систематическая погрешность — погрешность, изменяющаяся во времени по определённому закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором. Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора или если произошло замыкание в электрической цепи).

Грубые ошибки (промахи) возникают из-за

неправильного отсчета по прибору,

неисправности прибора, неправильной записи результата измерений или невнимательности

экспериментатора. Аккуратность при проведении эксперимента и использование исправной

измерительной техники позволяют избежать грубых ошибок.

Случайная погрешность — составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведенных в одних и тех же условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения, однако их влияние как правило можно устранить статистической обработкой. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики.

приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.

13. Методы оценки приборной и случайной погрешностей. Коэффициент Стьюдента. Методы оценки косвенных измерений. Примеры. Вычисление погрешностей. В дальнейшем будем предполагать, что

1) грубые погрешности исключены;

2) поправки, которые следовало определить (например, смещение нулевого деления шкалы), вычислены и внесены в окончательные результаты;

3) все систематические погрешности известны (с точностью до знака).

В этом случае результаты измерений оказываются все же не свободными от случайных погрешностей. Если случайная погрешность окажется меньше систематической, то, очевидно, нет смысла пытаться уменьшить величину случайной погрешности - все равно результаты измерений не станут значительно лучше и, желая получить большую точность, нужно искать пути к уменьшению систематической погрешности. Наоборот, если случайная погрешность больше систематической, то именно случайную погрешность нужно уменьшить в первую очередь и добиться того, чтобы случайная погрешность стала меньше систематической, с тем чтобы последняя опять определяла окончательную погрешность результата. На практике обычно уменьшают случайную погрешность до тех пор, пока она не станет сравнимой по величине с систематической погрешностью. Как будет видно из дальнейшего, случайная погрешность уменьшается при увеличении числа измерений.

Поскольку из-за наличия случайных погрешностей результаты измерений по своей природе представляют собой тоже случайные величины, истинного значения x ист измеряемой величины указать нельзя. Однако можно установить некоторый интервал значений измеряемой величины вблизи полученного в результате измерений значения xизм, в котором с определенной вероятностью содержится x ист. Тогда результат измерений можно представить в следующем виде:

где D x - погрешность измерений. Вследствие случайного характера погрешности точно определить ее величину невозможно. В противном случае найденную погрешность можно было бы ввести в результат измерения в качестве поправки и получить истинное значение xист.. Задача наилучшей оценки значения xист и определения пределов интервала (2) по результатам измерений является предметом математической статистики.

Для оценки случайной погрешности измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или средней квадратичной погрешности s (ее часто называют стандартной погрешностью или стандартом измерений).

Определим доверительный интервал. Чем большим будет установлен этот интервал, тем с большей вероятностью xист попадает в этот интервал. С другой стороны, более широкий интервал дает меньшую информацию относительно величины xист. Если ограничиться учетом только случайных погрешностей, то при небольшом числе измерений n для уровня доверительной вероятности a полуширина доверительного интервала (2) равна

где ta,n - коэффициент Стьюдента

коэффициенты Стьюдента— числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.

Механика