
- •2. Теоремы сложения и умножения вероятностей. Условные вероятности.
- •3. Дискретные случайные величины.
- •4.Непрерывные случайные величины.
- •5) Непрерывные и дискретные величины.
- •6. Непрерывные и дискретные случайные величины. Закон распределения Пуассона. Формулы для математического ожидания и дисперсии. Примеры.
- •7. Непрерывные и дискретные случайные величины. Плотность вероятности. Нормальный закон распределения. Математическое распределение и дисперсия. Графическое представление. Примеры.
- •8.Стандартное нормальное распределение
- •9. Понятие генеральной совокупности и выборки. Объём выборки, репрезентативность. Статистическое распределение (вариационный ряд). Примеры. Характеристики выборки
- •10. Оценка параметров генеральной совокупности по характеристикам её выборки (точечная и интервальная). (Параметры генеральной совокупности и характеристики выборки. Формулы, пояснения).
- •1Точечная
- •11 Графические характеристики случайных величин. Гистограмма. Характеристики положения (мода, медиана, выборочная средняя).
- •12. Прямые и косвенные измерения погрешности измерений абсолютная и относительная погрешности измерений систематическая приборная грубая случайная погрешности примеры
- •Вопрос 1.Мех волны
- •2. Звук.Виды звуков.Волнов.Сопротивление
- •4.Эффект доплера
- •9. Формула Стокса.
- •15.Закон Ома для переменного тока
- •17. Электрический диполь.
- •19.Токовый монополь. Токовый диполь. Электрическое поле токового
- •27. Принцип действия электронного усилителя, принципиальная схема на транзисторе.
- •29.Принцип работы электронного осциллографа.
- •30.Электроды для съема биоэлектрического сигнала
- •31. Датчики медико-биологической информации
- •32.Понятие об аналоговых, дискретных и комбинированных регистрирующих устройствах. Устройства отображения. Медицинское применение регистрирующих и отображающих устройств.
- •34.Частотная амплитудно-частотная характеристика усилителей. Линейные искажения. Полоса пропускания.
- •36Шкала электромагнитных излучений
- •40.Энергетические характеристики световых потоков, поток светового излучения и плотность потока(интенсивность). Волновая оптика. Дифракционная решетка. Дифракционный спектр.
- •42. Поляризация света.
- •43. Рассеяние света. Виды оптических неоднородностей. Показатель рассеяния. Закон Рэлея.
- •44.Поглощение света. Законы: Бугера, Бугера-Ламберта-Бара и тд.
- •46. Излучение Солнца.
- •48 Люминесценция. Спектры люминесценции…
- •49.Спектрофотометрия. Спектрофлуориметрия.
- •51. Виды радиоактивных излучений Радиоактивность.
- •54. Поглощённая и эквивалентная дозы ионизирующего излучения. Коэффициент качества для α-, β- ,μ-,
1. Случайное событие – событие, которое в ходе испытании может произойти, а может и не произойти
Классическое определение вероятности:
Вероятностью Р(А) случайного события А называется отношение кол-ва m элементарных событий А к общему кол-ву элементарных событий n.
Р(А)=m/n
Статистическое определение вероятности:
Вероятность – это число Рст(А), около которого группируются значения относительной частоты р*(А) наступления случ.события А при неограниченном возрастании кол-ва испытаний
Совместные события (А1,А2,А3…). Осуществление любого из них в рез-те испытания не исключает осуществления при этом любого другого из перечисленных событий.
Несовместные события (А1,А2,А3…). Осуществление любого из событий в рез-те испытания исключает осуществление при этом других перечисленных событий.
Зависимое событие. На его вероятность оказывает влияние исход какого-либо иного события.
Независимое событие. Б независимо от А, если появление или не появление события А не влияет на вероятность события Б.
2. Теоремы сложения и умножения вероятностей. Условные вероятности.
Теорема сложения: вероятность появления какого-либо события из нескольких несовместных равна сумме их вероятностей. P(A или B)=P(A)+P(B)
Теорема умножения: вероятность совместного появления независимых событий равна произведению их вероятностей. P(A и B)=P(A)*P(B)
Условная вероятность – вероятность некоторого события при условии того, что другое событие произошло, либо не произошло. Например, событие А произойдет при условии реализации события В. В таком случае используют обозначение Р(А/В).
Теорема умножения вероятностей для зависимых событий: вероятность наступления случайного события А и зависящего от него события В равна произведению вероятности события А на условную вероятность события В. P(A и B)=P(A)*P(B/А)
3. Дискретные случайные величины.
Распределением случайной величины называется зависимость вероятности её появления от численных значений этой величины.
Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случайных величин оно определяется, как сумма произведений случайной величины на вероятность ее появления:
![]()
Дисперсия описывает разброс случайных величин относительно математического ожидания. Дисперсия дискретных случайных величин определяется, как сумма произведений квадратов разности случайных величин и математического ожидания на соответствующие вероятности появления этих случайных величин:
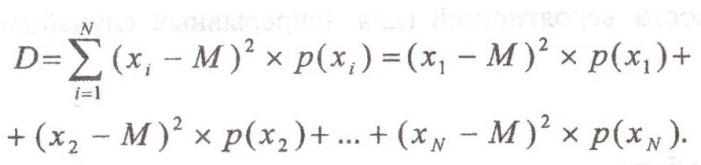
Средним
квадратическим отклонением
дискретной случайной величины называется
квадратный корень из ее дисперсии:
![]()
4.Непрерывные случайные величины.
Математическое ожидание: для непрерывных случайных величин - это операция интегрирования математич.ожидания для дискретных величин:
![]()
Дисперсия для непрерывных случайных величин:
![]()
Среднее квадратическое
отклонение, как и у дискретных:
![]()
5) Непрерывные и дискретные величины.
Случайной величиной, называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств.
Случайная величина называется дискретной, если она принимает счетное множество значений: число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека и т. д.
Непрерывная случайная величина принимает любые значения внутри некоторого интервала: температура воздуха за определенный промежуток времени, масса зерен в колосьях пшеницы, координата места попадания пули в цель( принимаем пулю за материальную точку) и т.д.
Биномиальный закон (распределение Бернулли)
В
общей форме биномиальный закон описывает
осуществление признака в ![]() испытаниях
с возвратом. Наглядной схемой таких
испытаний является последовательный
выбор с возвращением шаров из урны,
содержащей
испытаниях
с возвратом. Наглядной схемой таких
испытаний является последовательный
выбор с возвращением шаров из урны,
содержащей ![]() белых
и
белых
и ![]() чёрных
шаров. Если
чёрных
шаров. Если ![]() —
число появления белых шаров в выборке
из
—
число появления белых шаров в выборке
из ![]() шаров,
то
шаров,
то
![]()
где ![]() —
вероятность появления при одном
извлечении соответственно белого и
чёрного,
—
вероятность появления при одном
извлечении соответственно белого и
чёрного,![]() Производящая
функция биномиального распределения
задаётся формулой
Производящая
функция биномиального распределения
задаётся формулой![]() Основные
характеристики биномиального
распределения (математическое ожидание
и дисперсия)
Основные
характеристики биномиального
распределения (математическое ожидание
и дисперсия)![]() Пример
1. Вероятность
получения бракованного изделия равна
0,01. Какова вероятность того, что среди
100 изделий окажется не более 3 бракованных?
Пример
1. Вероятность
получения бракованного изделия равна
0,01. Какова вероятность того, что среди
100 изделий окажется не более 3 бракованных?
Решение. Пусть ![]() .
Согласно биномиальному закону и закону
сложения имеем
.
Согласно биномиальному закону и закону
сложения имеем![]()

