Статистика.

1.

Случайное событие – событие, которое в ходе испытании может произойти, а может и не произойти

Классическое определение вероятности:

Вероятностью Р(А) случайного события А называется отношение кол-ва m элементарных событий А к общему кол-ву элементарных событий n.

Р(А)=m/n

Статистическое определение вероятности:

Вероятность – это число Рст(А), около которого группируются значения относительной частоты р*(А) наступления случ.события А при неограниченном возрастании кол-ва испытаний

Совместные события (А1,А2,А3…). Осуществление любого из них в рез-те испытания не исключает осуществления при этом любого другого из перечисленных событий.

Несовместные события (А1,А2,А3…). Осуществление любого из событий в рез-те испытания исключает осуществление при этом других перечисленных событий.

Зависимое событие. На его вероятность оказывает влияние исход какого-либо иного события.

Независимое событие. Б независимо от А, если появление или не появление события А не влияет на вероятность события Б.

Статистика. Вопрос 2. Теоремы сложения и умножения вероятностей. Условные вероятности.

Теорема сложения: вероятность появления какого-либо события из нескольких несовместных равна сумме их вероятностей. P(A или B)=P(A)+P(B)

Теорема умножения: вероятность совместного появления независимых событий равна произведению их вероятностей. P(A и B)=P(A)*P(B)

Условная вероятность – вероятность некоторого события при условии того, что другое событие произошло, либо не произошло. Например, событие А произойдет при условии реализации события В. В таком случае используют обозначение Р(А/В).

Теорема умножения вероятностей для зависимых событий: вероятность наступления случайного события А и зависящего от него события В равна произведению вероятности события А на условную вероятность события В. P(A и B)=P(A)*P(B/А)

4.Непрерывные случайные величины.

Математическое ожидание: для непрерывных случайных величин - это операция интегрирования математич.ожидания для дискретных величин:

Дисперсия для непрерывных случайных величин:

Среднее квадратическое отклонение, как и у дискретных:

Мат.статистика-3. дискретные случайные величины.

Распределением случайной величины называется зависимость вероятности её появления от численных значений этой величины.

Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случайных величин оно определяется, как сумма произведений случайной величины на вероятность ее появления:

Дисперсия описывает разброс случайных величин относительно математического ожидания. Дисперсия дискретных случайных величин определяется, как сумма произведений квадратов разности случайных величин и математического ожидания на соответствующие вероятности появления этих случайных величин:

Средним квадратическим отклонением дискретной случайной величины называется квадратный корень из ее дисперсии:

Статистика. Вопрос 6. Непрерывные и дискретные случайные величины. Закон распределения Пуассона. Формулы для математического ожидания и дисперсии. Примеры.

Непрерывные величины принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения. Например, время, масса, объем.

Дискретные величины могут принимать конечное, счетное число случайных значений. Например, год рождения, число людей в автобусе, число страниц в книге.

Распределению Пуассона удовлетворяют вероятности появления заданного кол-ва редко происходящих случайных событий, наблюдаемый в серии из большого числа независимых опытов. Это распределение описывает дискретные, целочисленные неотрицательные случайные величины, появляющиеся с вероятностью р, много меньшей 1.

P_n(m)= /m!)* ,

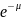Где m-число ожидаемых событий, P_n(m)-вероятность появления m искомых событий в серии из n независимых испытаний, μ-параметр распределения, совпадающий с математическим ожиданием, е-основание натурального логарифма.

Формулы для вычисления математического ожидания случайной величины.

Для дискретных величин M=∑Xi * Pi

Для непрерывных величин M=

Формулы для вычисления дисперсии случайной величины, среднеквадратического отклонения

Для дискретных величин D=∑(Xi-Xср)² * Рi

Для непрерывных величин D=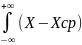 ² * f(x)dx

Среднеквадратическое отклонение δ=

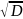
5) Непрерывные и дискретные величины.

Случайной величиной, называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств.

Случайная величина называется дискретной, если она принимает счетное множество значений: число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека и т. д.

Непрерывная случайная величина принимает любые значения внутри некоторого интервала: температура воздуха за определенный промежуток времени, масса зерен в колосьях пшеницы, координата места попадания пули в цель( принимаем пулю за материальную точку) и т.д.

Биномиальный закон (распределение Бернулли)

В общей форме биномиальный закон описывает осуществление признака в   испытаниях с возвратом. Наглядной схемой таких испытаний является последовательный выбор с возвращением шаров из урны, содержащей   белых и   чёрных шаров. Если   — число появления белых шаров в выборке из   шаров, то

где   — вероятность появления при одном извлечении соответственно белого и чёрного,

Производящая функция биномиального распределения задаётся формулой

Основные характеристики биномиального распределения (математическое ожидание и дисперсия):

Пример 1. Вероятность получения бракованного изделия равна 0,01. Какова вероятность того, что среди 100 изделий окажется не более 3 бракованных?

Решение. Пусть  . Согласно биномиальному закону и закону сложения имеем

Билет 7. Непрерывные и дискретные случайные величины. Плотность вероятности. Нормальный закон распределения. Математическое распределение и дисперсия. Графическое представление. Примеры.

Случайная величина (далее СВ) – величина, которая принимает значение в зависимости от стечения случайных обстоятельств. (Пр.: число больных на приеме врача, число студентов в аудитории, номер бочонка, когда его вынимают из мешка, при игре в лото и т.п.)

СВ называется дискретной (далее – ДСВ), если она принимает счетное множество значений. (Пр.: число букв на произвольной странице книге, число волос на голове человека, число молекул в выделенном объеме газа и т.п.)

СВ называется непрерывной (далее – НСВ), если она принимает любые значения внутри некоторого интервала. (Пр.: температура тела, масса зерен в колосьях пшеницы и т.п.)

Вероятность

- предел, к которому стремится частота события при неограниченном увеличении числа испытаний. (статистическое определение)

P(A)=lim_n→∞(m/n)

- отношение благоприятствующих случаев к общему числу равновозможных случаев к общему числу равновозможных несовместимых событий. (классическое опредедение) P(A)=(m/n)

Распределение вероятностей — закон, описывающий область значений СВ и вероятности их принятия.

1. Распределение ДСВ. Дискретная величина (Х) считается заданной, если указаны ее возможные значения (x_n) соответствующие им вероятности Р(х_n)=p_n. Совокупность Х и Р называется распределением ДСВ.

2. Распределение НСВ.

dP=f(x)dx

dP – вероятность того, что НСВ Х принимает значения между х и х+dх. Вероятность dP прямо пропорциональна интервалу dx.

f(x) – плотность вероятности (функция распределения вероятностей). Показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от самой этой величины.

f(x)=dP/dx

_x

F(x)=∫f(x)dx - функция распределения НСВ. Равна вероятности того, что СВ

^-∞

принимает значения, меньшие х.

F(x)=(-∞<X<x)

Нормальный закон распределения (закон Гаусса). СВ распределена по этому закону, если плотность вероятности имеет вид

a=M(X) – мат.ожидание СВ, σ – среднее квадратическое отклонение, σ²- дисперсия СВ.

Дисперсия СВ – МО отклонения случайной величины от ее МО.

D(X)=M[X-M(X)]

Удобная формула: D(X)=M(X²)-[M(X)]²

Кривая закона носит колокообразную форму, симметричную относительно прямой х=а (центр рассеивания). В точке х=а функция достигает максимума.

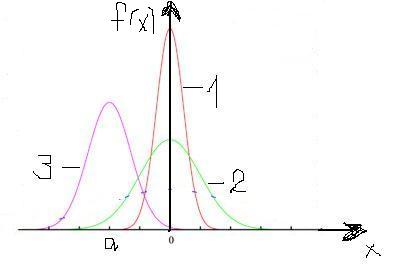
По мере возрастания |х-а| функция f(x) монотонно убывает, асимптотически приближаясь к нулю. С уменьшением σ кривая становится все более и более островершинной. Изменение а при постоянной σ не влияет на форму кривой, а лишь сдвигает ее вдоль оси абсцисс. Площадь, заключенной под кривой, согласно условию нормировки, равна единице. На рисунке изображены три кривые. Для кривых 1 и 2 а=0, но отличаются значением σ (σ₁<σ₂), кривая 3 имеет а≠0, σ=σ_2.

Вычислим функцию распределения.

Обычно используют иное выражение. Введем новую переменную t=(x-a)/σ. Следовательно, dx=σdt. Подставляем это в формулу.

Значение функции Ф(t) обычно находят в составных таблицах, так как интеграл через элементарные функции не выражается. График:

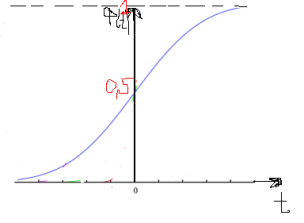
Случайная величина при нормальном распределении может находится в интервале (х₁, х₂). Вероятность этого равна

Р(х₁<x<х₂)=Ф((х₂-а)/σ)-Ф((х₁-а)/σ)

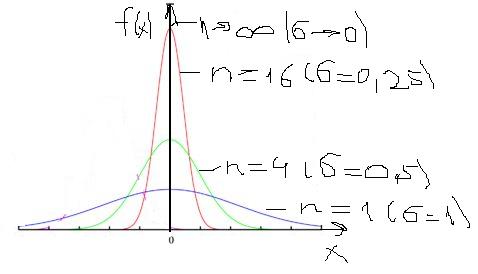
Допустим, что произвольно из нормальных распределений выбираются группы по n значений СВ. Для каждой группы можно найти средние значения (х₁, х₂, х_i). Они сами образуют нормальное распределение (только среднему значению будет соответствовать не вероятность, а относительная частота). МО будет соответствовать исходному, дисперсия и среднее квадратическое отклонение – отличаться в n и в √n соответственно.

D_n=D/n и σ_n=σ/√n.

На рисунке представлены графики нормальных распределений, полученных для групп со значением n, равными 1, 4, 16 и n→∞. При n=1 – исходное распределение, σ_n=σ. При n→∞ σ_n→0, фактически «группа СВ» - все исходное распределение, среднее значение выражается одним числом и соответствует МО, к которому сводится все распределение.