Осы теоремадан бейнесінің мынадай қасиетін алуға болады.
Егер
(3) теңсіздікте
шексіздікке ұмтылса, онда Лаплас
интегралының модулі нолге ұмтылады.
Осыдан
функциясы бейне болса, онда
(4)
болатындығы шығады.
Теорема 1.2 Бейненің қасиеті туралы
түпнұсқаның
бейнесі
шарты орындалатын жарты жазықтықта
аналитикалық функция болады.
Мұндағы
-түпнұсқаның
өсу көрсеткіші.
Анықтама
Мына
болса,
шартымен
анықталған
функциясы Хевисайдтың бірлік функциясы
деп аталады.
Осы
функциясы түпнұсқа болады. Оның өсу
көрсеткіші
.
Бұл функцияның мәні
болғанда анықталмаған, өйткені Лаплас
интегралын есептегенде
функциясының
болғанда қандай мән қабылдайтыны
ескерілмейді.
Дегенмен
де,
нүктесіндегі мәні үшін әдетте
мәндерін алады.
1
t
0
1.2 Сурет
Берілген
функциясы -
аралықта анықталсын және түпнұсқаның
(2), (3) шарттарын қанағаттандырсын. Ал
болғанда
шарты орындалсын. Егер
функциясын қарастырсақ, яғни
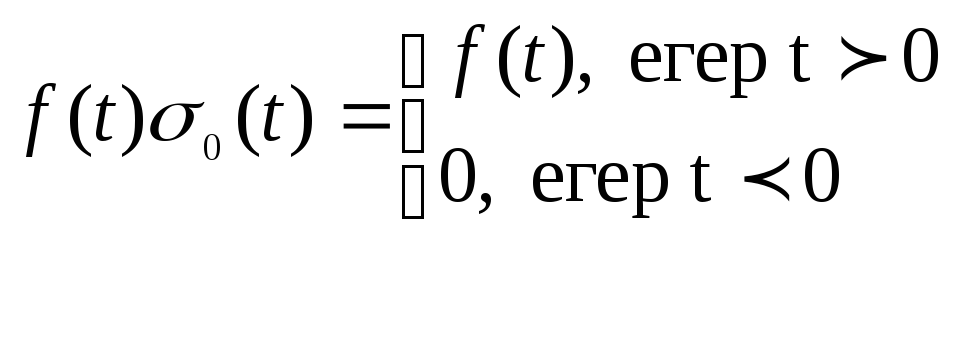болса,
(6)
онда
функциясы түпнұсқа болады. Мұндағы
көбейткіші
түпнұсқаның (1) шартының орындалуын
қамтамасыз етеді. Сондықтан, алдағы
уақытта
функциясының Лаплас түрлендіруінде
функциясы берілген деп есептеп, оның
орнына қысқаша
деп жазамыз.
Енді кейбір функциялардың бейнесін анықтама бойынша табу мысалдарын келтірейік.
1 Мысал
функциясының
бейнесін табу керек. Мұндағы
(нақты немесе комплекс сан).
Шешуі
Анықтама бойынша
Егер
деп алсақ, онда
Сондықтан, егер
болса, онда
болады. Нәтижесінде мынадай сәйкестік
аламыз:
Дербес жағдайда
2 мысал
функциясының
бейнесін табу керек.
Мұндағы
(нақты
немесе комплекс сан).
Шешуі
Егер
болса, онда
функциясының өсу көрсеткіші
егер
болса, онда
функциясы шектелген болады да
мәнін аламыз. Берілген функцияның Лаплас
түрлендіруін жазайық:
Мұндағы
ал
болсын. Олай болса
теңдігін аламыз. Осыдан, егер
болса, онда
мәні шығады.
Нәтижесінде
сәйкестігін аламыз.
Дербес жағдайда
(10)
(11)
Мұндағы ω-кез-келген комплекс сан.
3 мысал
функциясының
бейнесін табу керек.
Шешуі
болғандықтан,
функциясының өсу көрсеткіші
Берілген функцияның Лаплас түрлендіруін табайық
Егер
болса, онда
теңсіздігі алынады.
(Мұнда
)
Сонда
егер
болса, онда
аламыз.
Сондықтан
4 мысал
f(t)=cost функциясының бейнесін табу керек.
Шешуі
|cost
|
1
болғандықтанcost
функциясының
өсу көрсеткіші с
=0.
Бұл функцияның Лаплас түрлендіруін жазамыз:
Жақшаның ішіндегі функцияның шегі жоғарыда көрсетілгендей нолге ұмтылады. Сондықтан
1.3 Меллин формуласы
Берілген
бейнесінен оған сәйкес
түпнұсқасына көшу үшін Лапластың кері
түрлендіруі орындалады.
Теорема 1.3
Түпнұсқа
үздіксіздік нүктелерінде
теңдігімен анықталады.
Мұндағы
функциясы
түпнұсқасының Лаплас бойынша бейнесі.
(14) теңдіктің оң жағындағы интеграл бас
мәні ұғымында анықталады. Басқаша
айтқанда
арақатынасы
орындалады да, интеграл
жарты жазықтығында жатқан және жорымал
оське параллель түзу бойынша алынады.
(14)
формула Меллиннің кері айналдыру
формуласы деп аталады. Ол
бейнесі мен
түпнұсқасын байланыстырады.
Берілген
бейнесі бойынша түпнұсқаны табу Лапластың
кері түрлендіруі болып табылады. Оны
былай белгілейді:
Мұндағы
шарты
болғанда функцияның
шартын қанағаттандыратынын көрсетеді.
(14)
формула бейнені тек үздіксіздік
нүктелерінде ғана анықтайды. Бірақта
түпнұсқаның бірінші текті үзіліс
нүктелері болуы мүмкін.
Бұл
жағдайда түпнұсқаның
үзіліс нүктелерінде
шарты орындалатындығын көрсетуге болады.
Сонымен,
айналдыру формуласы
бейнесі бойынша
түпнұсқасы оның үзіліс нүктелеріндегі
мәндеріне дейінгі дәлдікпен анықталады.
Түпнұсқаға (1.1) формула бойынша анықталған
бір ғана бейне сәйкес келеді. Өйткені
түпнұсқаның үзіліс нүктелеріндегі
мәндері бейненің түрін өзгертпейді.
Дегенмен де бір бейнеге бір-бірінен
айырмашылығы үзіліс нүктелеріндегі
мәндерінде болатын түпнұсқалар жиынын
сәйкес қоюға болады.
Егер
түпнұсқасы
аралығында дифференциалданатын функция
болса, онда берілген бейне бойынша бір
ғана түпнұсқа анықталады.
Есептер
1. Мына функциялардың қайсысы түпнұсқа болатындығын тексеру керек
2. Мына функциялардың түпнұсқа болатындығын тексеріп, өсу көрсеткішін табу керек.
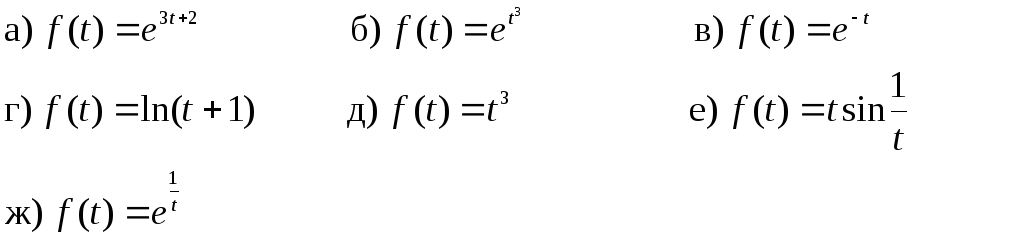
3. Лаплас интегралын пайдаланып мына функциялардың бейнесін табу керек.
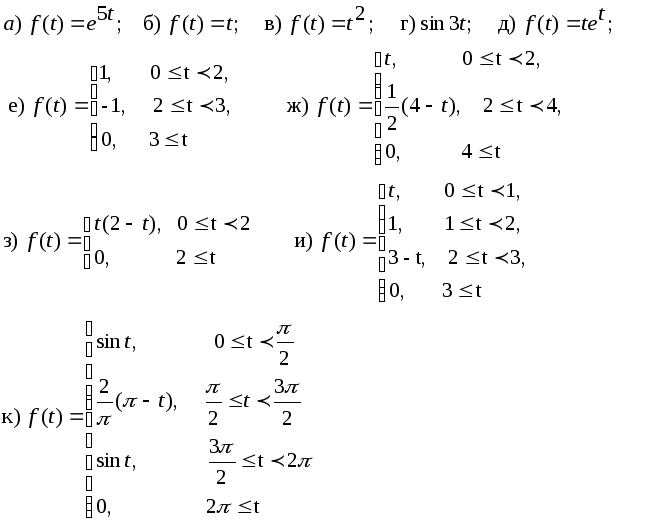
Жауаптары
1. а) иә; б) иә; в) жоқ; г) иә; д) иә; е) жоқ; ж) жоқ; з) иә; и) жоқ; к) иә.
2. а) иә, 3; б) жоқ; в) иә, 0; г) иә, 0; д) иә, 0; е) иә, 0; ж) жоқ.
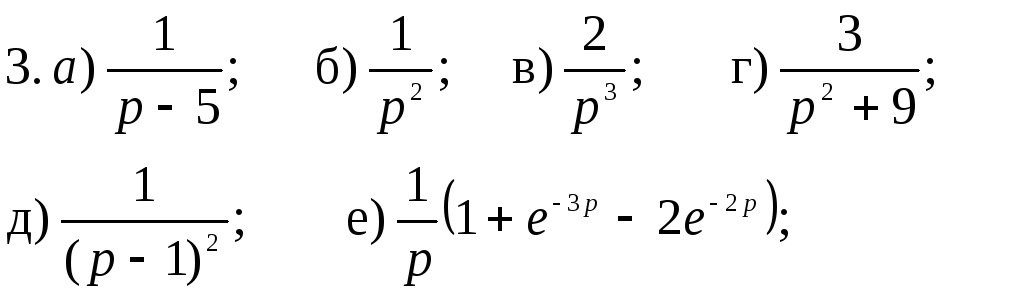
