32 Мысал

Тұрақты электр қозғаушы күші e(t)=E болатын энергия көзі қосылған суреттегі электр тізбегіндегі i(t) ток күшін табу керек. Алғашқы шарттар нөлге тең болып берілген

L C

е(t) R

4.1 сурет

Шешуі

болғандықтан (80) арақатынасын пайдаланып (81) табамыз.

Мұндағы 4.1 суретте берілген тізбектің Z(p) операторлық кедергісі нөлдік алғашқы шарттар бойынша мына түрде жазылады:

Осы өрнекті (81) формулаға қоямыз:

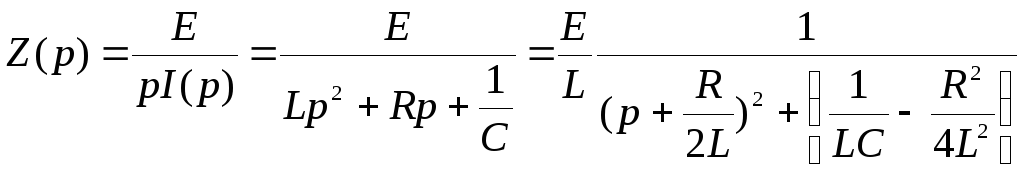(82)

Осы бейне бойынша i(t) түпнұсқасын табу үшін (82) теңдіктің оң жағындағы квадрат үшмүшеліктің түбірлерін зертттейміз.

Егер > болса, онда бейнелер кестесінен мынаны табамыз.

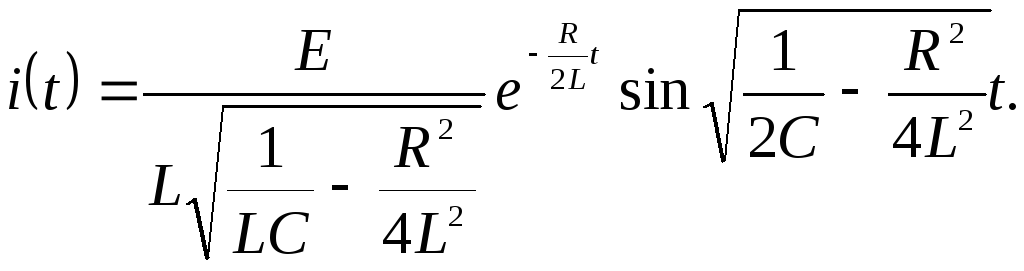
Егер = болса, онда бейнелер кестесінен пайдаланып

аламыз.

Егер < болса бейнелер кестесі бойынша

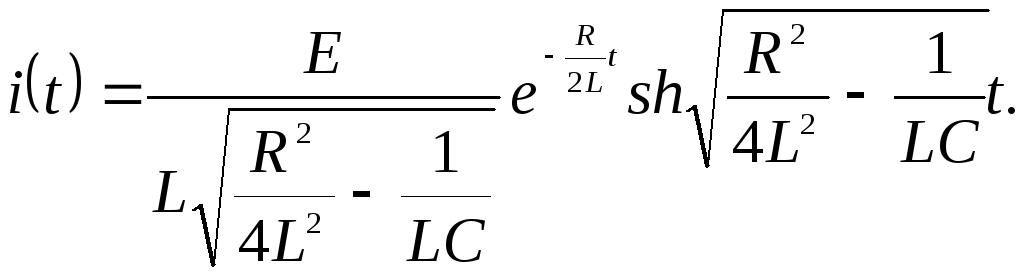
теңдігін аламыз.

4.6 Есептер

Алғашқы шарттары берілген мына дифференциалдық теңдеулерді шешу керек.

47. x^/+x=e^-t, х(0)=1

48. х^/-х=1, х(0)=-1

49. x^/+2x=sint, х(0)=0

50. x^/+3x=e^-2t, х(0)=0

51. x^/-3x=3t³+3t²+2t+1, х(0)=-1

52. x^/-x=cost-sint, х(0)=0

53. 2 x^/-6x=te^-3t, х(0)=-

54. x^/+x=2sint, х(0)=0

55. x^//=1, x(0)=0, х^/(0)=1

56. x^//+x^/=1, x(0)=0, х^/(0)=1

57. x^//+3x^/=e^t, x(0)=0, х^/(0)=-1

58. x^//-2x^/=e^2t, x(0)=х^/(0)=0

59. x^//+2x^/-3x=e^-t, x(0)=0, х^/(0)=1

60. x^//+2x^/+x=sint, x(0)=0, х^/(0)=-1

61. x^//+x^/=cost, x(0)=2, х^/(0)=0

62. x^//-x^/=1, x(0)=-1, х^/(0)=-1

63. x^//+x=t, x(0)=0, х^/(0)=1

64. x^//+6x^/=12t+2, x(0)=0, х^/(0)=0

65. x^//-2x^/+2x=2, x(0)=1, х^/(0)=0

66. 2x^//-2x^/=(t+1)e^t, ,

67. x^//+3x^/+2x=2t²+1, x(0)=4, х^/(0)=-3

68. x(0)=0

69. x^///-x^//=0, x(0)=1, х^/(0)=3, x^//(0)=2

70. x^///-4x^//=1, x(0)=0, 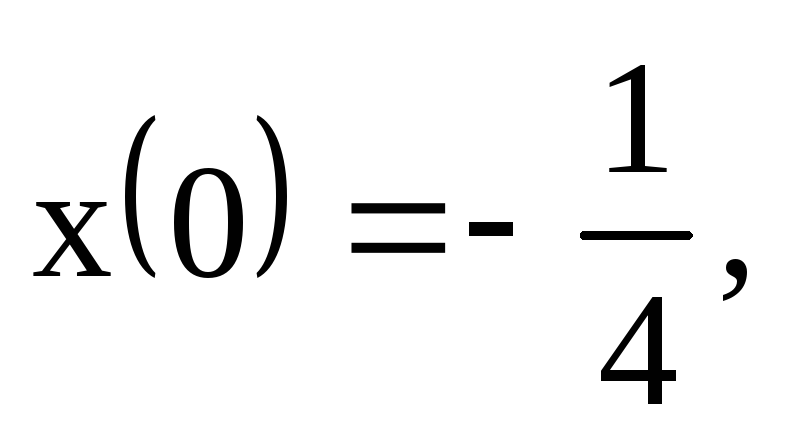x^//(0)=0

71. x^///+x^//-2x=5e^t, x(0)=0, х^/(0)=1, x^//(0)=2

72. x^//-4x^/=2cos²t, x(0)=0, х^/(0)=0

73. x^///+x=e^t, x(0)=0, х^/(0)=2, x^//(0)=0

74. x^//+4x=2cost cos3t, x(0)=x^/(0)=0

75. x^//+x=te^t+4sint, x(0)=x^/(0)=0

76. f(t)х^//+х=f(t),

х(0)=х¹(0)=0

1

0 1 2

-1

4.2 сурет

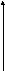f(t)

77.

2 х^//+4х=f(t),

х(0)=х^/(0)=0

0 1 2 t

4.3 сурет

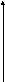
f(t)

78. х^//+9х=f(t),

х(0)=0, х¹(0)=1

1

.

0 1 2 3 t

4.4 сурет

79. f(t) х^//-2х¹+х=f(t),

х(0)=х¹(0)=0.

1

0 а 2а 3а

4.5 сурет

Дюамель формуласын пайдаланып мына теңдеулерді шешу керек.

80. х(0)=х^/(0)=0

81. х^//=arctgt, х(0)=х^/(0)=0

82. х^//=tln²t, х(0)=х^/(0)=0

83. х(0)=х^/(0)=0

84. х(0)=х^/(0)=0

85. х(0)=х^/(0)=0

86. х(0)=х^/(0)=0,87х^//-х=tht, х(0)=х^/(0)=0

Мына теңдеулер жүйесін операторлық әдіспен шешу керек.

88. 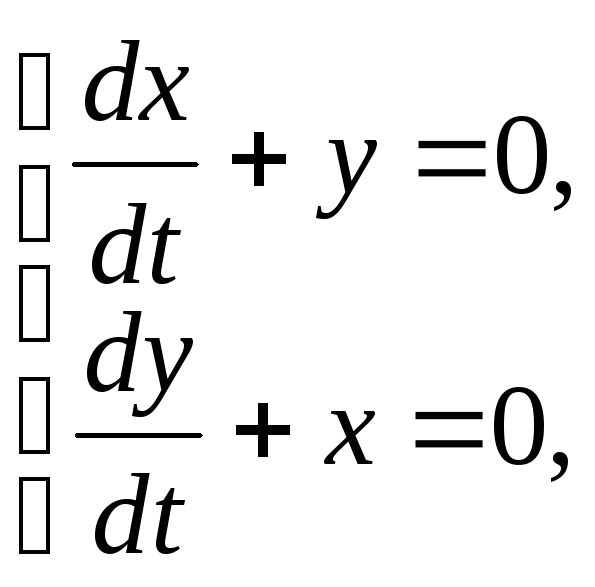х(0)=2, у(0)=0 89.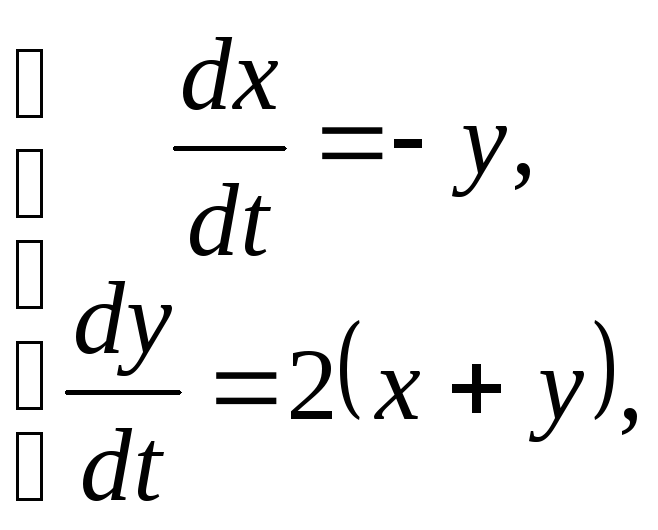 х(0)=у(0)=1

90. 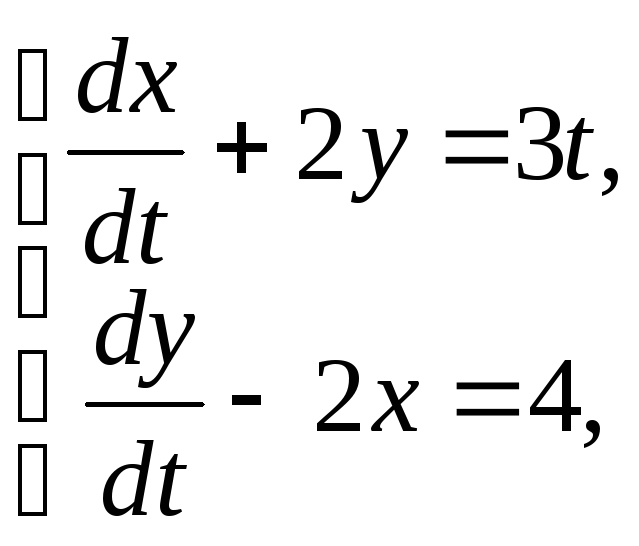х(0)=2, у(0)=3 91. х(0)=у(0)=1

92.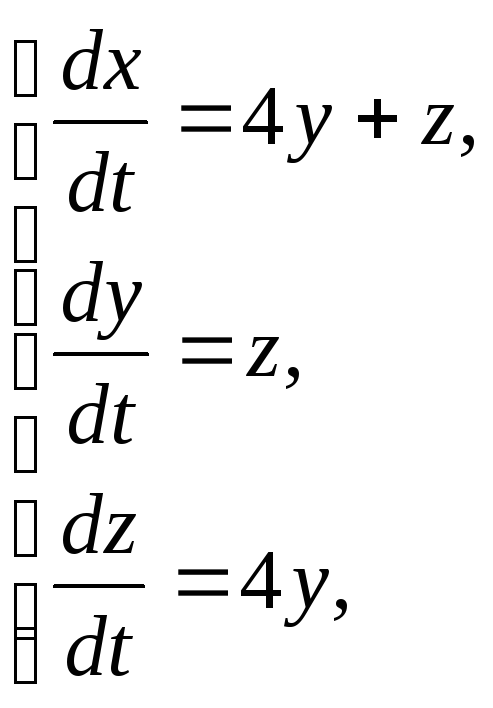x(0)=5, y(0)=0, z(0)=4.

93.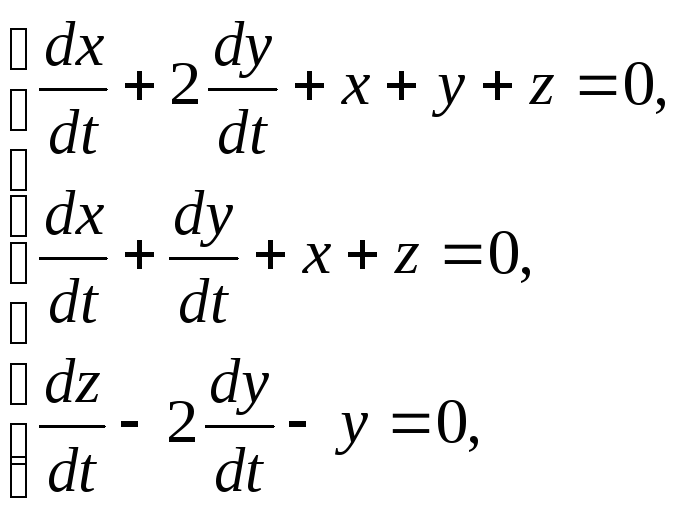x(0)=y(0)=1, z(0)=-2.

94. 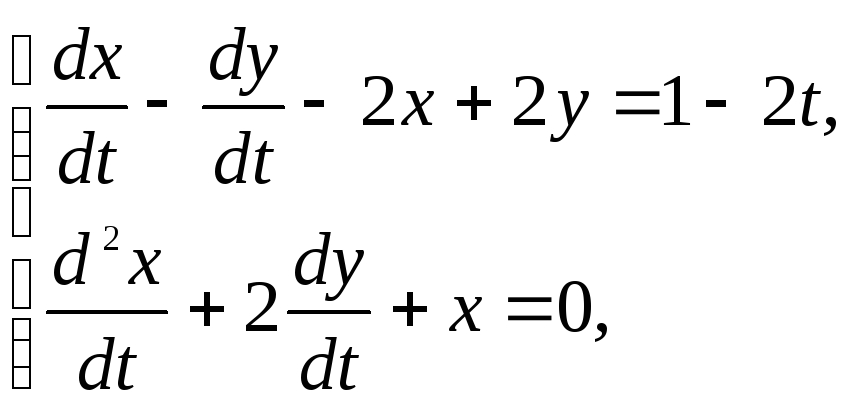x(0)=y(0)=x^/(0)=0.

95. 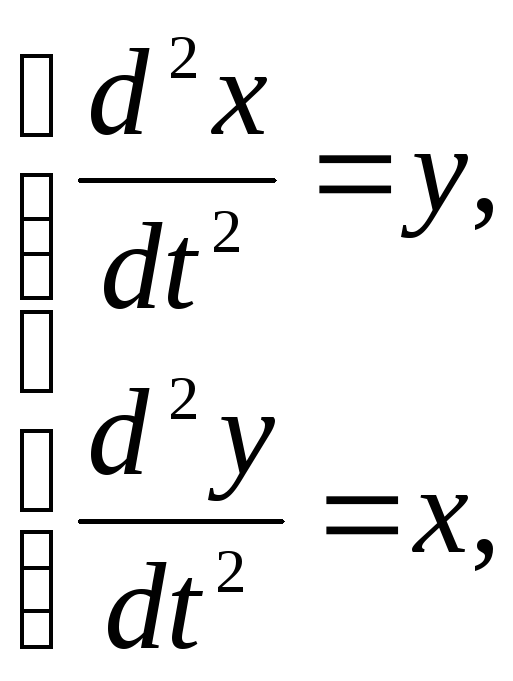x(0)=y(0)=1 x^/(0)=2, y^/(0)=2

96. 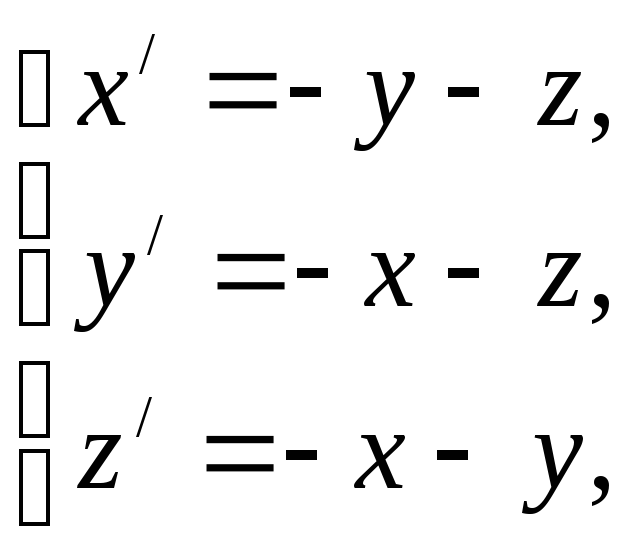x(0)=-1, y(0)=0, z(0)=1.

97. 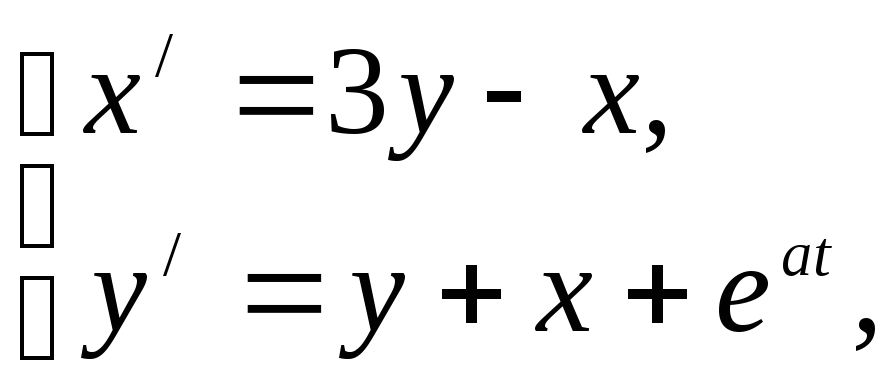x(0)=1, y(0)=1.

98. 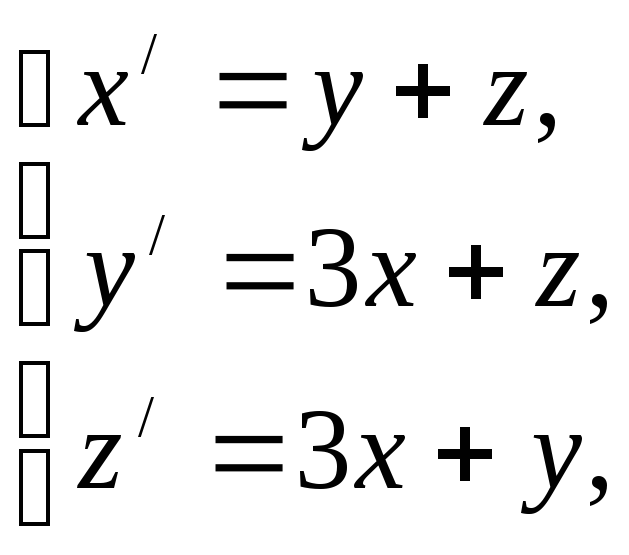x(0)=0, y(0)=1, z(0)=1.

99. 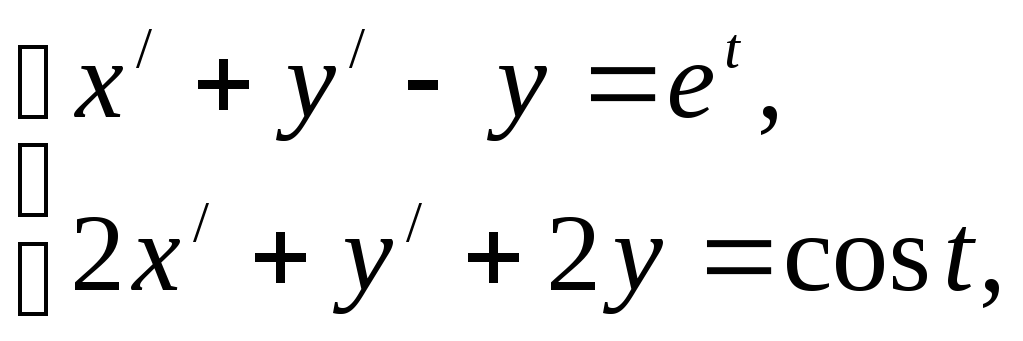x(0)=y(0)=0

Лаплас интегралының көмегімен мына меншіксі интегралдарды есептеу керек.

100. а) б) в)

г) д) е)

101. Мына меншіксіз интегралдарды (79) формуланың көмегімен есептеу керек.

а) >0

б) a>0, b>0

102.

R

4.6 сурет