STROITEL_NOE_MATERIALOVEDENIE_RYB_EV

3.3.ПОДОБИЕ ОПТИМАЛЬНЫХ СТРУКТУР И ДВЕ ТЕОРЕМЫ В ТЕОРИИ ИСК

Воснове моделирования исследований и общих законов изменения свойств в теории ИСК лежит важное научное положение о подобии оптимальных структур. Имеется в виду подобие геометри ческое, физическое и технологическое. Как известно, фундаментальные работы в области теории подобия выполнены Бертраном Н.С., Кирпичевым В.Л., Афанасьевой Т.А., Кирпичевым М.В., Седовым Л.И., Гухманом А.А., Вениковым В.А. и др. Были разработаны и убедительно доказаны три теоремы о подобии систем, а также о соответствующем их моделировании.

Геометрическое подобие в этой теории устанавливается при условии равенства сходственных углов и пропорциональности сходственных длин у геометрических фигур одинаковой формы. В оптимальных структурах искусственных конгломератов,

размещающихся на гиперболических кривых MN1 или параболических кривых MN2 (см. рис. 3.8), в качестве таких геометрических фигур выступают континуальные пленки связующего вещества или матрицы. Вдоль упомянутых гиперболической или параболической кривых оптимальных структур отношение толщин δ/ δ * этих пленок, умножаемых на соответствующие коэффициенты масштабов подобия, остаются пропорциональными величинами. Другой геометрической фигурой практически одинаковой формы вдоль упомянутых кривых оптимальной структуры выступают сферические поры. С увеличением заполняющей части в конгломерате диаметр пор возрастает, что фиксируется с помощью коэффициентов масштабов подобия, как это было в случае отношений толщин пленок. Количество пор (пористость в единице объема) вдоль кривой оптимальных структур остается практически одинаковым (2—3%). Наличие этих двух сходственных элементов структуры и их количественных пропорциональностей фиксирует геометрическое подобие оптимальных структур.

Геометрическому подобию оптимальных структур сопутствует их физическое подобие. Физические явления, процессы или системы подобны, если сходственные величины, характеризующие состояние системы (в данном случае — оптимальной структуры) пропорциональны соответствующим величинам другой системы (т. е. другой оптимальной структуры конгломерата).

Для доказательства физического подобия оптимальных структур в теории ИСК используется ее первая теорема. Имеются два произвольных ИСК оптимальной структуры

— А и Б. В отношении каждого из них действуют закономерности, которые ранее были установлены для материалов с конгломератным типом структуры. Требуется доказать, что конгломерат А физически подобен конгломерату Б. Для доказательства возможно использовать каждую из трех теорем, известных в теории подобия, или привлечь всех их вместе.

Согласно теореме подобия в формулировке М.В. Кирпичева (известной как первая теорема теории подобия), «подобные явления описываются буквенно-одинаковыми уравнениями, которые условно или безусловно инвариантны по отношению к подобным преобразованиям входящих в них величин». Известно, что в теории ИСК одинаковыми буквенными уравнениями описываются прочность и вне зависимости от напряжения, которое она выражает, деформативность и, в частности, величина упругих, не пластических (т. е. обратимых) деформаций. Соответствующей им величиной выражается и модуль упругости. В буквенные сходственные выражения уравнений входят подобные и притом инвариантные физические величины как характеристики оптимальных структур вяжущего вещества (матрицы) и качества заполняющего компонента конгломератов. Так,

например, по условию доказываемой теоремы прочность конгломерата А

что обе эти формулы являются апостериорными. Однако, исходя из подобия, возможно априори написать, что прочность еще одного конгломерата, например В, будет равна:

«подобные явления описываются буквенно одинаковыми уравнениями» и, следовательно, принятые по условию конгломераты А, Б, В оптимальной структуры геометрически и физически подобны между собой, что и требовалось доказать.

Для доказательства первой теоремы теории ИСК можно воспользоваться и второй теоремой теории подобия, называемой также Пи-теоремой и в свое время доказанной Бэкингемом, Т.А. Афанасьевой и др. В ней при подобии явлений и систем устанавливается связь не только между реальными размерными — именованными — величинами, как по первой теореме М.В. Кирпичева, но и между их безразмерными комбинациями, именуемыми критериями подобия.

инвариант подобия, а величина c / фn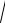R / R* — как критерий подобия. Все числовые

значения являются безразмерными, что полностью удовлетворяет условиям Пи-теоремы, а следовательно, конгломераты А и Б физически (при ранее отмеченном геометрическом подобии) подобны между собой, что и требовалось доказать.

Для доказательства первой теоремы ИСК можно воспользоваться и третьей теоремой теории подобия, выведенной М.В. Кирпичевым и А.А. Гухманом. Она устанавливает следующие необходимые и достаточные условия для подобия явлений и систем: геометрическое подобие, буквенная одинаковость уравнений (т. е. соблюдение первой теоремы теории подобия). Достаточным условием является равенство определяющих критериев подобия (т. е. вторая теорема теории подобия) или равенство единице критерия подобия, называемого тогда индикатором подобия. Выше показано, что в теории ИСК принят индикатор подобия А, предложенный И.А. Рыбьевым:

При оптимальных структурах А = 1 и, следовательно, согласно третьей теореме теории подобия, конгломераты (в данном случае конгломераты А и Б) оптимальных структур подобны между собой, что и требовалось доказать.

Подобие структур сохраняется не только в данный момент, но и в течение времени, т. е. оно носит временной характер. Следует только обеспечить необходимую долговечность ИСК по его структурным и, следовательно, экстремальным качественным показателям. Временной характер подобия в теории ИСК указывает на технологическое подобие конгломератов оптимальной, структуры.

Цементные бетоны, асфальтобетоны, пластмассы, строительные растворы, древесностружечные плиты и т. п. применяют в конструкциях нередко в виде сложных сочетаний в системах, в которых отдельные конгломераты выступают в качестве подсистем. Однако и в этом случае каждый материал в системе должен иметь по возможности свою оптимальную структуру, поскольку тогда обеспечивается наилучшее качество всей конструкции. Согласно теореме В.А. Веникова, если подобны подсистемы, то оказываются подобными и сами системы. Следовательно, материалы оптимальной структуры не только подобны между собой, но и образуют в целом систему (строи- тельную конструкцию) наилучшего качества, что способствует эффективному решению многих инженерных задач.

Кроме первой теоремы о подобии конгломератов оптимальной структуры, в теории ИСК имеется еще и вторая теорема — о правомерности закона конгруэнции для конгломератов

92

оптимальной структуры, изготовленных не только на общем, но и на основе различных вяжущих веществ. Выше, в 3.2.2, закон конгруэнции сформулирован в его полном объеме, однако его третья часть утверждения осталась недоказанной. Поэтому требуется доказать, что существует обязательное соответствие свойств между конгломератами оптимальной структуры при различных числовых значениях вяжущих веществ, а также показать масштабный критерий подобия в общем уравнении.

Для доказательства написано уравнение прочности конгломерата при первом вяжущем веществе:

Rиск1 = R1* / x1n1 .

То же — для второго вяжущего вещества: Rиск2 = R2* / x2n2 .Решая эти два

уравнения применительно к первому или второму конгломератам, находится формула (3.3), показанная ранее в 3.2.2. Из той же формулы (3.3) следует, что масштабным показателем подобия является отношение расчетных характеристик принятых вяжущих

веществ, т. е. безразмерная величина, равная (R2* / R1* ), или ей обратная. Понятно, что

присутствие масштабного показателя не нарушает доказательства первой теоремы о подобии конгломератов оптимальных структур.

93

3.4. НАУЧНЫЕ ПРИНЦИПЫ И ОБЩИЙ МЕТОД ПРОЕКТИРОВАНИЯ СОСТАВА ИСК ОПТИМАЛЬНОЙ СТРУКТУРЫ

Оптимизацию структуры и научно-обоснованное определение вещественного состава различных искусственных конгломератов осуществляют общим (единым) методом проектирования. Могут быть методы и специфические, разработанные применительно к каждой разновидности конгломерата. Некоторые специфические особенности выделяются и при применении общего (единого) метода. Однако остаются неизменными научные принципы, лежащие в основе проектирования состава любым методом. К главным науч- ным принципам относятся: наибольшее приближение технологических режимов и параметров, используемых в лабораторной практике проектирования состава, к реальной технологии производства конгломератной смеси и изделий; обеспечение возможно большей равномерности распределения частиц разной крупности, пор, поверхностей раздела фаз и других структурных элементов по объему материала; обеспечение заданных свойств на уровне числовых значений экстремумов при оптимальной структуре; применение общих объективных закономерностей, присущих конгломератным матери- алам оптимальной структуры и, в том числе, закона конгруэнции, закона створа, закона прочности и других; использование общего метода и средств проектирования оптимального состава, и точная реализация проектного состава на производстве.

Практическая цель проектирования заключается в определении расхода исходных компонентов (по массе) на одну тонну или один кубический метр плотной смеси. После формования, уплотнения и отвердевания смесь приобретает оптимальную структуру ИСК, которому придана форма изделия или конструкции, используемых при монтаже зданий и сооружений в строительстве.

Реализация общего метода проектирования оптимального состава ИСК является существенной частью технологического процесса, которая в свою очередь является гарантом высшего качества изготовляемой продукции в соответствии с полученным проектным составом. Этот метод включает три этапа.

Рис. 3.14. Зависимость насыпной плотности смеси заполнителей (ρн) от содержания в ней песка (П)

Первый этап предусматривает выполнение ряда исходных операций: обоснование главных показателей строительно-эксплуатационных свойств конгломерата, исходя из тщательного анализа реальных условий работы его в конструкциях; выбор исходных материалов, соответствующих их функциональному назначению как компонентов конгломерата; определение или проверка, если были указаны, технических свойства принятых материалов с привлечением стандартных нормативов и с учетом производственных или назначаемых по проекту технологических параметров и режимов. Для ответственных строительных объектов результаты первого этапа проектирования

94

состава конгломерата могут быть рассмотрены совместно со строительной организацией (заказчиком) как своеобразное техническое задание.

Второй этап — расчетно-экспериментальный и предназначен для определения расхода принятых компонентов на одну тонну, или на 1 м3, или на другое количество смеси (например, на один замес смеси в объеме смесительного аппарата). Он выполняется в определенной последовательности операций, исходя из основных зависимостей в их математических выражениях, которые можно использовать в программах, реализуемых в дальнейшем с помощью машинной техники. Первая операция в этой последовательности

— определение расчетной активности принятого вяжущего вещества и минимального фазового отношения, т. е. R* и с*/ф. Впрочем, определение расчетной активности более часто относят к первому этапу проектирования состава при технической оценке исходных материалов. Вместо прочности может быть принято другое свойство материала — упругая деформация, плотность, вязкость, морозостойкость и т. п., в зависимости от назначения ИСК. Второй операцией на этом этапе проектирования служит определение состава плотной смеси заполнителя ρн (рис. 3.14). Третья и наиболее емкая операция — выявление количества исходных компонентов в смеси, из которой формуют конгломерат. Она выполняется с помощью формул и расчетных характеристик, безмашинным способом или с привлечением электронно-вычислительных машин. При необходимости определяют показатели тех же свойств при других значениях Т и ν.

Третий этап — изготовление пробного замеса проектного состава, по возможности в производственных условиях, например в смесительном цехе завода. С помощью лабораторных испытаний устанавливают качество смеси и отформованного конгломерата по всем предусмотренным свойствам. Особо устанавливают наличие оптимальной структуры, например по индикатору подобия или по кривым оптимальных структур. Если отмечены отклонения, то производят корректирование состава. Последнее может потребоваться и при выпуске массовой продукции на заводе, если исходные материалы получают время от времени другого состава и других свойств, чем были приняты в лаборатории на стадии проектирования состава.

Ниже детализируется рациональная последовательность проектирования состава ИСК в общем виде с изложением в некоторых последующих главах конкретных примеров при безмашинном и машинном способах.

Первый этап: определение расчетной активности вяжущего вещества (R*) как матричной части ИСК и минимального значения с*/ф, обеспечивающего при принятых технологических параметрах оптимальную структуру. Для этого из смеси вяжущего вещества с 3—4 различными с/ф, отличающимися между собой обычно на величину 0,02—0,05, изготовляют образцы, установленные стандартами при оценках свойств испытуемого материала. Для первых прикидочных опытов образцы могут приниматься меньших размеров в целях экономного расходования исходных компонентов. После всех испытаний и графического построения функции R =f(с/ф) находят и, при необходимости, уточняют искомое значение с*/ф при наибольшей прочности вяжущего вещества R*.

На первом этапе устанавливают также состав плотной смеси заполнителя (крупного — К и мелкого — М) расчетным или, что чаще, экспериментальным путем с определением соотношения по массе величины М/К.

Второй этап начинается с уточнения конкретных математических зависимостей, которыми предстоит воспользоваться в расчетах по составу конгломератной смеси. Здесь потребуется выполнить также две операции, одна из которых является вспомогательной (экспериментальной), другая — основной (расчетной).

Вспомогательная операция необходима для определения показателей степени n и m, используемых в формулах прочности и составов. Для этого по лабораторным данным строят кривую оптимальных структур (рис. 3.15) при произвольно выбранном значении (с/ф)A в точке А на этой кривой. Находят величину RА на кривой ДВЕ, а также значение (с+ф)B в точке В. Прочность RА имеется и на кривой KL, которой к началу эксперимента

95

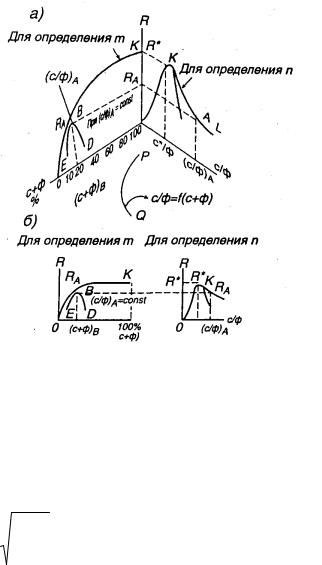
хотя еще и нет, но о ее вероятном существовании, как кривой оптимальных структур на плоскости х—у из теории ИСК известно. И тогда полученных данных RА, (с/ф)B, (с/ф) достаточно, чтобы определить значения показателей степени n и m, согласно формулам (3.3) и (3.4), поскольку другие требуемые значения R* и с*/ф уже были определены на

Рис. 3.15. Графики кривых оптимальных структур в пространственной системе координат R=f(с/ф; с+ф) (а)

и на плоскостях R=f1(с/ф); R=f2(с+ф1); с/ф=f3(с+ф1) (б); с+ф=100–(п+щ) в %

Здесь важно учитывать, что величина n является постоянной, тогда как m — переменная, требующая корректирования для других значений с/ф или R. На этом вспомогательная операция второго этапа завершена. Следует переход к основной операции этого этапа — начислению количества расходов компонентов в проектном составе смеси. Рациональная последовательность расчетов:

а) искомое фазовое отношение вяжущего вещества, пользуясь формулой (3.4), а именно:

как определяется при новом значении (с/ф)иск, а не при прежнем (с/ф)А, а именно:

96

mx = m ((c / ф))иск ;

c / ф А

в) искомое количество жидкого компонента с на 1 т смеси:

с = (с + ф)иск (с/ ф)иск 10 кг/т; 1 + (с/ ф)иск

г) искомое количество дисперсного твердого компонента смеси на 1 т:

д) искомое количество заполнителя: М+К=100 – (с+ф)иск; е) искомое количество мелкого компонента в заполнителе при ранее найденном отношении М/К, а именно:

M = (M + K ) M / K 10 кг/т; 1 + M / K

ж) искомое количество крупного компонента в заполнителе:

K = M + K 10 кг/т. 1 + M / K

Все найденные значения с, ф, М, К умножены на 10 потому, что в 1 т (1000 кг) каждый 1% составляет 10 кг.

При необходимости производят перерасчет массы компонентов на 1 м3 конгломератной смеси (без учета воздушных пор) в следующей последовательности:

а) определение абсолютных объемов исходных материалов (при условии, что известны или были найдены на первом этапе проектирования значения их истинных плотностей δс, δф, δM и δK), необходимых для образования 1 тонны смеси (л):

10·с/δс; 10·ф/δф; 10·M/δM; 10·К/δК;

б) определение средней плотности конгломератной смеси (кг/м3):

в) определение материалов на 1 м3 конгломератной смеси (кг/м3):

жидкой среды: с·γиск; твердой фазы: ф·γиск;

мелкого заполнителя: М·γиск; крупного заполнителя: К·γиск.

Третий этап: приготовление контрольного замеса (лучше в производственных условиях) с оценкой его качественных характеристик. При необходимости корректируют проектный состав с учетом влажности используемых минеральных компонентов смеси. Запро- ектированный и откорректированный состав передают на производство для использования его в строительстве.

97

3.5. КОРРЕКТИРОВАНИЕ ПРОЕКТНОГО СОСТАВА ИСК

Проектный состав является правильным до тех пор, пока материалы, применяемые на заводе, соответствуют требованиям, которые были приняты на стадии проектирования. В производственных условиях они, однако, могут отклоняться как по составу, так и по свойствам, поэтому необходим не только строгий текущий контроль за качеством используемых материалов, но и оперативное корректирование проектного состава конгломерата. Возможны три случая:

1. Изменились свойства вяжущего или его отдельных компонентов, если вяжущее по своему составу является сложным. В этом случае в заводской лаборатории необходимо определить новую величину расчетной активности вяжущего и соответствующее ей фазовое отношение (R* при с*/ф) и, пользуясь формулой (3.3), вычислить новое фазовое

формулой (3.4) — новое количество вяжущего вещества при этом фазовом отношении:

c / ф

где n и m = mx (с/ ф)А — числовые значения показателей степени, определяемые

опытным путем, о чем сообщалось выше — при выполнении вспомогательной операции на втором этапе проектирования состава.

Далее производится пересчет содержания каждого компонента на 1 т или на 1 м3 конгломератной смеси.

2.Изменились заполняющие материалы, хотя они продолжают отвечать общим техническим требованиям. В этом случае можно подобрать новое соотношение фракций заполнителя с выявлением нового соотношения (по массе) между мелким и крупным заполнителями (например, П/Щ) при наибольшей плотности их смеси. А затем при любом, практически удобном отношении с/ф определяют экспериментальным путем

новые показатели степеней n и mx, а расчетным путем — новые оптимальные значения с/ф и с+ф. Далее пересчитывают прежний номинальный состав на новый, откорректи- рованный.

3.Изменились все исходные материалы. В этом случае скорректировать состав можно путем определения новой величины расчетной активности вяжущего вещества и новых

показателей степени n и mx. После этого по формулам (3.3) и (3.4), исходя из закона обязательного соответствия свойств (конгруэнции), определяют оптимальное отношение с/ф в конгломерате и новое количество вяжущего вещества с+ф.

Во всех трех случаях весьма целесообразно пользоваться заранее подготовленными таблицами или графиками в соответствующих координатных осях (с/ф — % вяжущего вещества, n — с/ф и др.).

Аналогичным образом корректируют оптимальный состав, когда изменяются в производственных условиях технологические параметры и режимы, а также когда влага в заполнителе засчитывается как часть жидкой среды в проектном составе.

98

3.6. СОЗДАНИЕ НОВЫХ СТРОИТЕЛЬНЫХ КОНГЛОМЕРАТОВ

Общая теория ИСК способствует не только существенному повышению качества и совершенствованию технологий с переводом их в прогрессивные на уровне мировых достижений, но и созданию новых строительных материалов с конгломератным типом структуры. Именно поэтому в единой классификации предусмотрены вакантные «клетки». Каждая из них может быть в свою очередь центром развития своеобразной группы конгломератов определенной разновидности. Однако эти группы и отдельные конгломераты в них продолжают оставаться связанными с единой классификацией ИСК общей теорией, общими закономерностями оптимальных структур.

Создание новых строительных конгломератов основывается на открытых закономерностях, количество которых возрастает по мере развития строительного материаловедения как фундаментальной науки прикладного характера. Оно осуществляется по определенной системе, в которой исходные положения прогнозирования сочетаются с новыми экспериментальными исследованиями. Среди основных положений прогнозирования следующие:

всегда неизбежен качественный скачок к оптимальной структуре конгломерата и переход, через экстремум показателей свойств по мере количественного накопления дисперсионной среды в системе с переходом ее из дискретного в континуальное пленочное состояние на поверхности твердой фазы; оптимальная структура конгломерата возможна при любом заполнителе, хотя наиболее

экономичными и технически рациональными являются составы с максимальной плотностью упаковки его частиц и, следовательно, с наименьшим расходом вяжущего вещества в конгломерате; с достаточной степенью приближения к истине целесообразно принимать, что линия

оптимальных структур конгломератов на графике R(с/ф) описывается гиперболической зависимостью у = а/хb, в которой все члены имеют строго определенный физический смысл; вдоль кривой оптимальных структур размещается бесчисленное множество створов с

наиболее благоприятным комплексом показателей строительных и эксплуатационных свойств. Проектирование состава позволяет выбрать один или несколько рациональных по технико-экономическим показателям; самой наглядной и полной формулой прочности ИСК оптимальной структуры является

(3.6). В ней нашли отражение практически все его структурные элементы в их теснейшей взаимосвязи.

Постадийное осуществление творческого процесса создания новых видов ИСК заключается в следующем.

Первая стадия включает детальное изучение вероятного вяжущего вещества. Для этого вначале потребуется установить главные технические требования к конгломератному материалу с тем, чтобы он обеспечивал надежность и долговечность изготовляемой из него конструкции в эксплуатационный период. По комплексу показателей конгломерата судят в первом приближении о необходимых свойствах вяжущего вещества как будущей матричной части и выбирают наиболее подходящее вяжущее из числа традиционных. Важно учесть характер эксплуатационных условий работы конгломерата в конструкции. Часто именно от этих условий зависит выбор неорганического или органического вяжущего вещества с последующим уточнением их конкретной разновидности из числа традиционных.

Сложнее тот случай, когда при разработке нового ИСК не имеется в наличии традиционного вяжущего вещества.и приходится ориентироваться на его получение по аналогии с традиционными технологиями или вовсе оригинального продукта и т. п. С помощью лабораторных испытаний изучаются с разной степенью полноты (от прикидочных да уточненных) свойства создаваемых композиций по некоторым условно

99

принятым технологиям с последующим их корректированием. Постепенным увеличением базового отношения с/ф достигают экстремального значения требуемого (ключевого) свойства, ранее принятого для конгломерата. Если определяющими свойствами конгломерата являются прочность и какое-либо другое свойство, например теплосопротивление, то выясняются показатели обоих свойств вяжущего. При необходимости понижения теплопередачи можно предусмотреть использование поризующих средств, но с учетом допустимого снижения прочности вяжущего (его рас- четной активности при оптимальной структуре). Если важно сохранить в определенных пределах обратимые деформации — упругие и упруго-вязкие (эластические), то эти свойства вяжущего также изучают при оптимальной структуре. Процесс изучения сырья для вяжущего основывается на законах створа и конгруэнции свойств. Необходимые средства улучшения ключевых показателей качества — введение дополнительных ингредиентов, катализаторов, отвердителей, соединение с традиционными вяжущими веществами, использование технологических приемов (измельчение, механико- химическая обработка, тепловая обработка, перемешивание и др.). Далее выясняют отдельные детали технологии изготовления вяжущего вещества, предлагают методы оценки его качества, сходные с принятыми при оценке конгломератов.

На второй стадии создания нового строительного конгломерата определяют возможную разновидность заполнителя, что также обусловлено сырьевыми ресурсами, проектными требованиями к свойствам ИСК, разновидностью вяжущего вещества (порошкообразный, компаунд, расплав и т. п.) и уровнем его вероятной адгезионной способности по отношению к предполагаемому заполнителю. Устанавливают рациональный род заполнителя — минеральный или органический, порошкообразный, зернистый или волокнистый, тяжелый, плотный или легкий, пористый. Учитывают также другие возможные пожелания к качеству; цвет — при изготовлении конгломератного материала для отделочных штукатурок, теплопроводность — при изготовлении теплоизоляционно- конструктивного материала и т. п. Одновременно решают вопрос о целесообразных форме и размере частиц заполнителя, плотности заполняющей смеси.

Наиболее экономичными являются, как отмечалось, составы с максимальной плотностью упаковки плотных или пористых частиц заполнителя и, следовательно, с наименьшим расходом вяжущего вещества. Этот принцип приобретает тем большее значение, чем ближе оптимальная структура к контактной. Вместе с тем максимальная плотность не может быть самоцелью, а должна назначаться в совокупности с экономическими подсчетами, с учетом фазового отношения вяжущего вещества (с его увеличением целесообразно повышение количества мелкозернистой фракции в заполнителе), наличием материалов и т. п.

Вопрос о минимально допустимой прочности заполнителя также решается с позиций общей теории1. Его актуальность возрастает по мере снижения прочности заполнителя по сравнению с прочностью создаваемого ИСК. При решении вопроса о минимальной прочности камня как заполнителя принимают во внимание релаксационный процесс, который тем эффективнее снижает внутреннее напряженное состояние, чем меньше период релаксации матричного материала. И тогда появляется дополнительная воз- можность снижения минимально допустимой прочности камня, используемого для изготовления заполнителя. Период или время релаксации матричного вещества оценивается при соответственных условиях, т. е. при оптимальных структурах и

1 Рыбьев И.А., Скрыльников Д.К. О минимально допустимой прочности каменного материала, применяемого в асфальтовом бетоне // Изв. ВУЗов. Разд. Строительство и архитектура. Новосибирск. 1972, вып. 5.

Рыбьев И.А., Голованова .Л.В. Релаксация напряжений в асфальтобетоне оптимальной структуры // Изв. ВУЗов. Разд. Строительство и архитектура. Новосибирск. 1974, вып. 10.

100