Лекція 13 (Іванова Ю.І

Застосування методів диференціальних рівнянь

в економічних моделях

1. Модель демографічного процесу

Зі статистичних даних відомо, що для даного регіону кількість новонароджених і померлих за одиницю часу пропорційна чисельності населення з коефіцієнтами пропорційності і відповідно. Знайдемо закон зміни чисельності населення в часі, інакше кажучи, опишемо демографічний процес у регіоні.

Нехай - кількість мешканців регіону в момент часу . Приріст населення за час дорівнює різниці між кількістю народжених і кількістю померлих за цей час, тобто

або ,

Де .

Переходячи до границі при , дістанемо рівняння

. (1)

Це диференціальне рівняння першого порядку з відокремленими змінними. Розв’яжемо його:

,

, (2)

Де - довільна стала, що визначається початковими умовами (чисельністю населення в початковий момент часу).

2. Модель рівноважного зростання

випуску продукції

Нехай продукція деякої фірми продається за фіксованою ціною . Позначимо через обсяг продукції, реалізованої в момент часу . Тоді на цей момент часу дістанемо доход . Припустимо, що частина доходу використовується на інвестиції у виробництво реалізованої продукції, тобто

, (3)

Де - норма інвестицій (стале число), причому .

Якщо виходити з припущення про не насичення ринку (тобто про повну реалізацію продукції, що виробляється), то в результаті розширення виробництва буде одержано приріст доходу, частина якого знову використовуватиметься для розширення випуску продукції. Це приведе до зростання швидкості випуску продукції (акселерації) , причому швидкість випуску пропорційна збільшенню інвестицій, тобто

, (4)

Де - норма акселерації. Підставивши (4) у (3), дістанемо

або

, (5)

де

Рівняння (5) – це диференціальне рівняння першого порядку з відокремленими змінними, загальний розв’язок якого , де - довільна стала.

Нехай у початковий момент часу обсяг продукції становить . Тоді .

Виразимо сталу : і підставимо її значення в загальний розв’язок. Дістанемо частинний розв’язок рівняння (4), тобто розв’язок задачі Коші

. (6)

Зазначимо, що математичні моделі мають властивість загальності. Так, рівняння (6) описує також динаміку росту цін за постійної інфляції, процес розмноження бактерій, процес радіоактивного розпаду.

3. Модель зростання випуску продукції

в умовах конкуренції

Припустимо, що деяка фірма випускає продукцію й продає її за ціною за одиницю. Позначимо через обсяг продукції, яка реалізована в момент часу . Нехай ціна залежить від обсягу продукції. Тоді - спадна функція, тобто зі збільшенням обсягу випуску продукції її ціна на ринку зменшується. Це означає, що У момент часу фірма одержує доход . Якщо частина доходу використовується на інвестиції у виробництво реалізованої продукції, то за умови не насиченості ринку швидкість випуску продукції пропорційна збільшенню інвестицій, тобто , де - це норма інвестицій, - норма акселерації, - стала ціна.

У випадку, коли ціна , дістанемо диференціальне рівняння першого порядку відносно із відокремленими змінними

, (7)

де . Оскільки всі співмножники в правій частині цього рівняння додатні, то й , тобто функція зростаюча. Характер зростання функції визначається її другою похідною. Диференціюючи рівняння (7), дістанемо

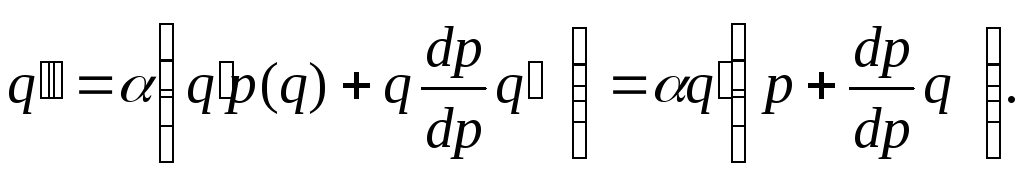(8)

Оскільки еластичність попиту , то рівність (8) можна записати у вигляді

.

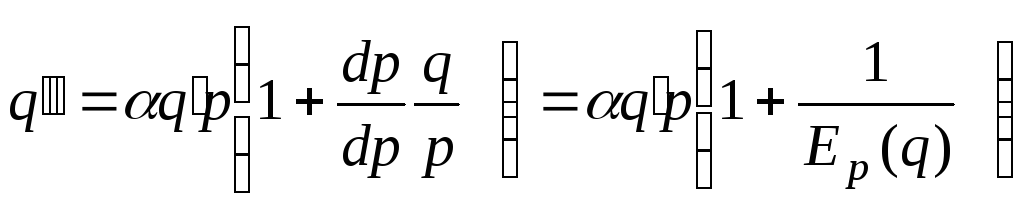Ураховуючи, що , а отже, й , остаточно дістанемо

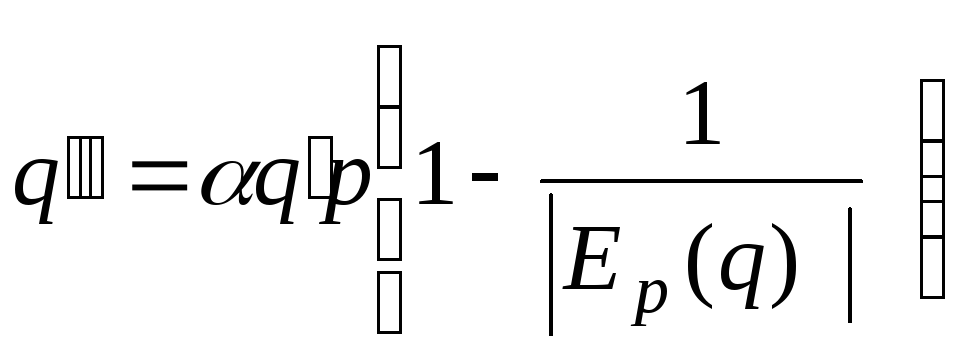. (9)

Із рівності (12.58) випливає, що за еластичного попиту, тобто коли , графік функції має напрям опуклості вниз, а це означає прогресивне зростання; за нееластичного попиту, тобто при , графік функції має напрям опуклості вгору, що означає вповільнене зростання (насичення).

Розглянемо залежність ціни від попиту у вигляді лінійної функції

(10)

Тоді рівняння (7) і (9) набирають вигляду

(11)

І

(12)

Відповідно.

Зі співвідношень (11) і (12) дістанемо, що при і при при . Отже, - точка перегину графіка функції .

Графік функції - однієї з інтегральних кривих диференціального рівняння – називають логістичною кривою.

3