
- •Інтегральне числення функцій однієї змінної (конспект лекцій)
- •Таблиця інтегралів
- •Заміна змінної в невизначеному інтегралі (метод підстановки)
- •4.Інтегрування частинами у невизначеному інтегралі
- •Інтегрування раціональних функцій
- •Інтегрування деяких ірраціональних функцій
- •7. Інтегрування деяких виразів, що містять тригонометричні функції
- •8. Використання таблиць інтегралів
- •9. Поняття про інтеграли, що не виражаються через елементарні функції
- •10. Приклади задач, що приводять до поняття визначеного інтеграла
- •2)Задача про шлях точки у прямолінійному русі.
- •11. Означення визначеного інтеграла
- •12. Основні властивості визначеного інтеграла
- •13. Інтеграл як функція верхньої межі. Формула Ньютона-Лейбніца
- •14. Метод заміни змінної у визначеному інтегралі
- •15. Інтегрування частинами у визначеному інтегралі
- •16. Загальна схема застосування визначеного інтеграла
- •17. Обчислення площі плоскої фігури
- •18. Обчислення довжини дуги
- •19. Обчислення об’єму тіла
- •20. Обчислення площі бічної поверхні тіла обертання
- •21. Обчислення роботи змінної сили
- •22. Обчислення сили тиску рідини на вертикальну пластину
- •23. Невластивий інтеграл по нескінченному проміжку
- •24. Ознаки збіжності невластивого інтеграла по нескінченному проміжку
- •25. Невластивий інтеграл від необмеженої функції
- •26. Ознаки збіжності невластивого інтеграла від необмеженої функції
- •27. Наближене обчислення визначених інтегралів
15. Інтегрування частинами у визначеному інтегралі
Теорема.
Якщо функції
![]() і
і
![]() мають неперервні похідні на відрізку
мають неперервні похідні на відрізку
![]() , то
, то
 ,
,
або
коротше
 .
.
Оскільки
функція
![]() є первісною для функції
є первісною для функції
![]() , то за формулою Ньютона-Лейбніца
, то за формулою Ньютона-Лейбніца
 .
.
Звідси на підставі властивості лінійності визначеного інтеграла отримуємо
 ,
,
що й треба було довести. Ця формула називається формулою інтегрування частинами у визначеному інтегралі.
Приклади.
1) Обчислити

Покладемо
![]() ,
,![]() ,
,![]() .
Тоді
.
Тоді

 .
.
Обчислити
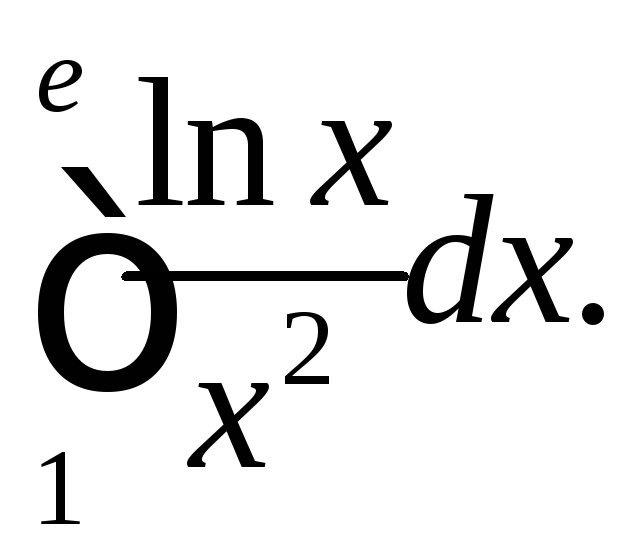

16. Загальна схема застосування визначеного інтеграла
В
багатьох задачах геометричного і
фізичного змісту шукана величина може
бути подана як приріст деякої функції
![]() на заданому відрізку
на заданому відрізку
![]() ,
тобто як
,
тобто як
![]() .
Згідно з формулою Ньютона-Лейбніца
.
Згідно з формулою Ньютона-Лейбніца

Отже
для обчислення величини такого типу
необхідно знайти вираз диференціала
![]() відповідної функції
відповідної функції
![]() і проінтегрувати його на відрізку
і проінтегрувати його на відрізку
![]() .
Диференціал
.
Диференціал
![]() з точністью до нескінченно малих вищого
порядку дорівнює приросту
з точністью до нескінченно малих вищого
порядку дорівнює приросту
![]() на малому («елементарному») відрізку
на малому («елементарному») відрізку
![]() ,
тобто малій частинці («елементу») шуканої
величини. Тому такий підхід до застосування
інтеграла в практичних задачах називають
іноді методом «вилучення елемента». В
подальшому ми розглянемо використання
цього методу на прикладах ряду конкретних
задач.
,
тобто малій частинці («елементу») шуканої
величини. Тому такий підхід до застосування
інтеграла в практичних задачах називають
іноді методом «вилучення елемента». В
подальшому ми розглянемо використання
цього методу на прикладах ряду конкретних
задач.
Існує
і інший підхід до розв’язання аналогічних
задач. Він полягає в тому, що шукану
величину наближено виражають у вигляді
інтегральної суми для деякої функції
![]() і деякого розбиття відрізка
і деякого розбиття відрізка![]() .
В міру подрібнення розбиття точність
цього виразу зростає, і в границі він
прямує до точного значення шуканої
величини, тобто до інтеграла
.
В міру подрібнення розбиття точність
цього виразу зростає, і в границі він
прямує до точного значення шуканої
величини, тобто до інтеграла
 .
Це так званий «метод інтегральних сум».
.
Це так званий «метод інтегральних сум».
Прикладом його застосування може служити задача про площу криволінійної трапеції, розглянута раніше як одна з задач, що приводять до поняття визначеного інтеграла.
Надалі при розгляді прикладів застосування інтеграла ми користуватимемося методом вилучення елемента.
17. Обчислення площі плоскої фігури
1) Плоска фігура, обмежена лініями, рівняння яких задані в декартовій системі координат.
Р
Рис. 4![]()
![]() ,
обмежену графіками функцій
,
обмежену графіками функцій![]() і
і
![]() і прямими
і прямими![]() і
і![]()
![]() .
Площа
.
Площа![]() цієї фігури дорівнює різниці площ
криволінійних трапецій
цієї фігури дорівнює різниці площ
криволінійних трапецій![]() і
і![]() ,
отже
,
отже
Якщо
значення
![]() і
і![]() не задані, то межі інтегрування
визначаються як абсциси точок перетину
ліній
не задані, то межі інтегрування
визначаються як абсциси точок перетину
ліній![]() і
і![]() .
.
Приклад.
Обчислити площу, обмежену параболами
![]() і
і
![]() .
.
Знайдемо точки перетину цих кривих. Координати цих точок задовольняють рівняння обох парабол, тобто систему

Віднімаючи від другого рівняння
Рис. 5![]()
![]() або
або![]() .
.
Рис. 5![]()
![]() ,
,![]() .
Тоді
.
Тоді
Рис. 5
![]()
 =
=
Рис. 3![]()

2) Плоска фігура, обмежена лініями, рівняння яких задані в полярній системі координат.
 Розглянемо
спочатку криволінійний сектор, тобто
фігуру, обмежену променями
Розглянемо
спочатку криволінійний сектор, тобто
фігуру, обмежену променями
![]() і
і![]() і кривою
і кривою![]() ,
де
,
де![]() - неперервна функція (див. рис. 6).
- неперервна функція (див. рис. 6).
Рис. 6![]()
![]() і відповідний йому промінь. Розглянемо
площу тієї частини криволінійного
сектора, яка розташована між променем
і відповідний йому промінь. Розглянемо
площу тієї частини криволінійного
сектора, яка розташована між променем![]() і променем, що відповідає обраному
значенню
і променем, що відповідає обраному
значенню![]() .
Кожному
.
Кожному![]() відповідає певне значення цієї площі,
тобто ці площа є функція від
відповідає певне значення цієї площі,
тобто ці площа є функція від![]() ,
задана на
,
задана на![]() .
Позначимо її
.
Позначимо її![]() . При цьому
. При цьому![]() , а
, а![]() ,
де
,
де![]() - площа всього криволінійного сектора.
Таким чином
- площа всього криволінійного сектора.
Таким чином

Приріст
![]() на малому відрізку
на малому відрізку
![]() зображується площею заштрихованого на
рисунку сектора, а ця площа з точністю
до нескінченно малих вищого порядку
дорівнює площі кругового сектора радіуса
зображується площею заштрихованого на
рисунку сектора, а ця площа з точністю
до нескінченно малих вищого порядку
дорівнює площі кругового сектора радіуса
![]() з центральним кутом
з центральним кутом
![]() :
: +
нескінченно малі вищого порядку.
+
нескінченно малі вищого порядку.
Тоді
 ,
а площа даного криволінійного сектора
виражається формулою
,
а площа даного криволінійного сектора
виражається формулою
 .
.
Тепер
розглянемо загальніший випадок, коли
фігура обмежена  променями
променями
![]() і
і
![]() та лініями
та лініями
![]() і
і
![]()
![]() .
(див. рис. 7, фігура
.
(див. рис. 7, фігура
![]() ).
Функції
).
Функції![]() і
і
![]() гадаються неперервними. Площа заданої
фігури
гадаються неперервними. Площа заданої
фігури
![]() дорівнює очевидно різниці площ
криволінійних секторів
дорівнює очевидно різниці площ
криволінійних секторів![]() і
і![]() :
:
Рис. 7
![]()
Об’єднуючи інтеграли в правій частині, одержуємо формули для площі заданої фігури:
 .
.
Приклади:
а) Знайти площу, обмежену кардіоїдою
![]() .
.
Рис. 8
![]()
![]() дорівнює подвоєній площі
дорівнює подвоєній площі![]() криволінійного сектора (заштрихований
на рисунку), обмеженого променями
криволінійного сектора (заштрихований
на рисунку), обмеженого променями![]() і
і![]() та кривою
та кривою![]() .
Тоді
.
Тоді

Рис. 8
![]()

Рис. 9![]()
 б)
Знайти площу частини фігури, обмеженої
кардіодою
б)
Знайти площу частини фігури, обмеженої
кардіодою 
![]() ,
яка лежить зовні кола
,
яка лежить зовні кола![]() .
Внаслідок симетрії шукана площа
.
Внаслідок симетрії шукана площа![]() дорівнює подвоєній площі
дорівнює подвоєній площі![]() фігури, обмеженої променями
фігури, обмеженої променями![]() і
і
 та
кривими
та
кривими![]() і
і![]() .
Тоді
.
Тоді




