20. Обчислення площі бічної поверхні тіла обертання

Рис. 15

Розглянемо поверхню, утворену обертанням навколо осідуги лінії, деі неперервні на відрізку . Перетнемо поверхнюдвома площинами, які проходять через точкиі перпендикулярно до осі . Частина поверхні, яка міститься між цими площинами є «кільце», ширина якого з точністю до нескінченно малих вищого порядку дорівнює елементу довжини дуги , а довжина його розгортки (довжина кола радіуса

). Площа поверхні цього кільця з точністю до нескінченно малих вищого порядку дорівнює і це є диференціал шуканої площі поверхні обертання. Тоді при змінівіддоплоща поверхні дорівнює

Приклад. Знайти площу поверхні, утвореної обертанням навколо осі дуги лінії на відрізку

Знаходимо Тоді

21. Обчислення роботи змінної сили

Нехай під дією сили матеріальна точка рухається прямолінійно вздовж осі . Позначимо проекцію сили на вісь через .

Рис. 16

Потрібно обчислити роботу, виконану цією силою при переміщенні

точки з положення в положення . Робота, виконана силою на елементарному відрізку, з точністю до нескінченно малих вищого порядку дорівнює(добуток сили на переміщення). Тоді робота, виконана на всьому відрізку, дорівнює .

Приклад. Обчислити роботу, яка виконується при стисканні пружинного амортизатора на 6 см, якщо для його стискання на 1 см потрібна сила 100 . Стиск амортизатора пропорційний прикладеній силі.

За умовою сила і стискпропорційні, тобто, де . При за умовою , тому , звідки . Отже , .

Тоді робота дорівнює Дж.

22. Обчислення сили тиску рідини на вертикальну пластину

Рис. 17

Потрібно обчислити силу тиску рідини на вертикальну стінку резервуара, греблю чи шлюз, тощо. Оберемо систему координат так, щоб її початок знаходився на вільній поверхні рідини, вісьбула спрямована перпендикулярно до вільної поверхні вглиб рідини, а плоска фігура , силу тиску на яку потрібно обчислити, лежала в площині. Нехай ця фігура обмежена лініямиіта прямимиі, де функціїінеперервні на відрізку.

Згідно з законом Паскаля тиск рідини на глибині дорівнює, де- густина рідини,- прискорення сили тяжіння. Перетнемо задану фігуру прямими, які проходять через точкиіперпендикулярно до осі . Площа виокремленої елементарної смужки з точністю до нескінченно малих вищого порядку дорівнює , а тиск, що діє на неї дорівнює, так що диференціал сили, діючої на пластину, дорівнює, а при змінівіддосила, прикладена до пластини, дорівнює

.

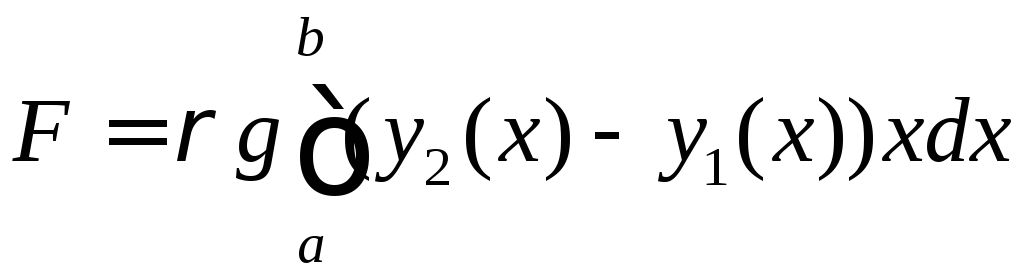Приклад. Знайти силу тиску рідина на фігуру , обмежену вільною поверхнею рідини (тобто віссю ) і параболою(параболічний сегмент).

Рис. 18

В даному випадку ,,, так що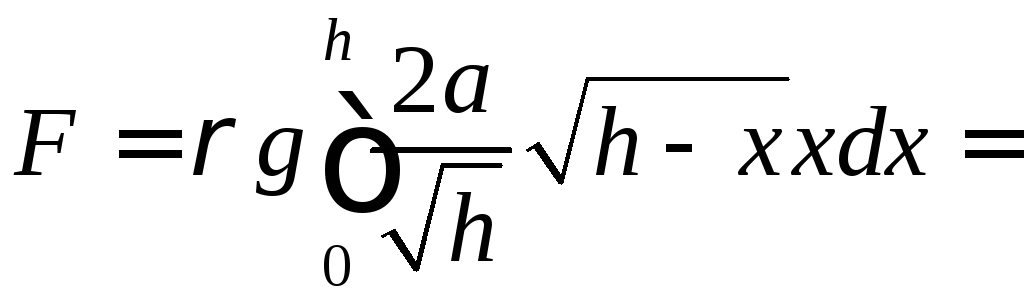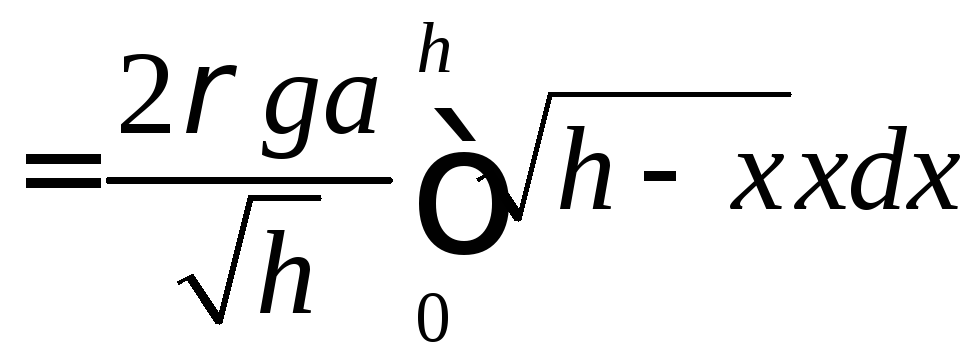. Зробимо підстановку:, тоді

, , при ,, прибуде.

Тоді

23. Невластивий інтеграл по нескінченному проміжку

В означенні інтеграла припускалося, що проміжок інтегрування скінченний, а підінтегральна функція обмежена на цьому проміжку. Тим часом застосування інтеграла іноді вимагають узагальнення цього поняття на випадок нескінченного проміжка або випадок необмеженої підінтегральної функції. Такі інтеграли називають невластивими.

Означення. Нехай функція визначена на проміжкуі інтегровна на будь-якому проміжку, де, тобто інтеграл

існує для будь-якого значення . Якщо існує скінченна границя

, то ця границя називається невластивим інтегралом від

функції по нескінченному проміжку і позначається.

Рис. 19

В такому разі кажуть, що даний невластивий інтегралзбігається. В противному разі кажуть, що невластивий інтеграл розбігається і символу ніякого числового значення не приписують. Якщо функціяневід’ємна , то збіжний інтегралможна тлумачити як скінченну площу нескінченної фігури, обмеженої віссю, прямоюі графіком функції.

Цілком аналогічно визначається невластивий інтеграл від функції по нескінченному проміжку:.

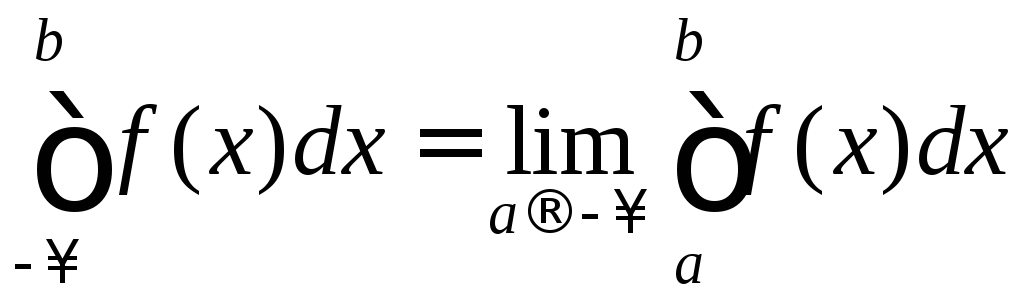Іноді розглядається невластивий інтеграл по всій числовій прямій . За означенням, де- будь-яке число, при умові, що обидва інтеграли в правій частині збігаються.

Приклади. Обчислити невластивий інтеграл або довести його розбіжність.

а)

Інтеграл збігається.

б)

Пропонуємо читачеві пересвідчитися, що при даний інтеграл розбігається. Таким чином інтегралзбігається, якщоі розбігається, якщо.