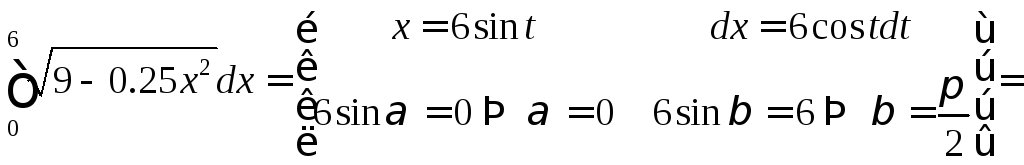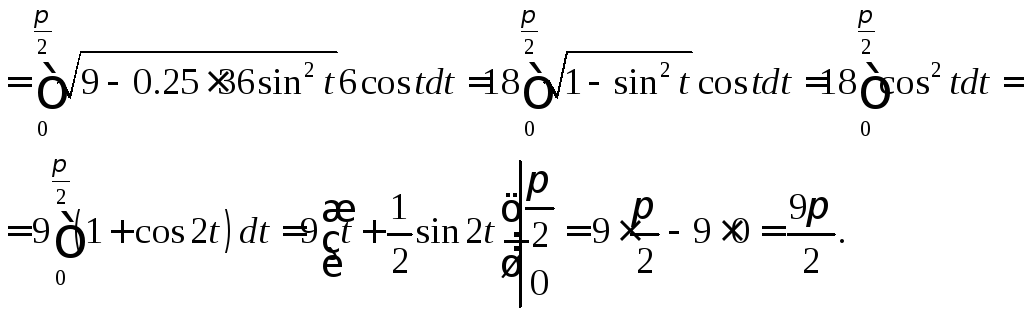- •Інтегральне числення функцій однієї змінної (конспект лекцій)
- •Таблиця інтегралів
- •Заміна змінної в невизначеному інтегралі (метод підстановки)
- •4.Інтегрування частинами у невизначеному інтегралі
- •Інтегрування раціональних функцій
- •Інтегрування деяких ірраціональних функцій
- •7. Інтегрування деяких виразів, що містять тригонометричні функції
- •8. Використання таблиць інтегралів
- •9. Поняття про інтеграли, що не виражаються через елементарні функції
- •10. Приклади задач, що приводять до поняття визначеного інтеграла
- •2)Задача про шлях точки у прямолінійному русі.
- •11. Означення визначеного інтеграла
- •12. Основні властивості визначеного інтеграла
- •13. Інтеграл як функція верхньої межі. Формула Ньютона-Лейбніца
- •14. Метод заміни змінної у визначеному інтегралі
- •15. Інтегрування частинами у визначеному інтегралі
- •16. Загальна схема застосування визначеного інтеграла
- •17. Обчислення площі плоскої фігури
- •18. Обчислення довжини дуги
- •19. Обчислення об’єму тіла
- •20. Обчислення площі бічної поверхні тіла обертання
- •21. Обчислення роботи змінної сили
- •22. Обчислення сили тиску рідини на вертикальну пластину
- •23. Невластивий інтеграл по нескінченному проміжку
- •24. Ознаки збіжності невластивого інтеграла по нескінченному проміжку
- •25. Невластивий інтеграл від необмеженої функції
- •26. Ознаки збіжності невластивого інтеграла від необмеженої функції
- •27. Наближене обчислення визначених інтегралів
13. Інтеграл як функція верхньої межі. Формула Ньютона-Лейбніца
Нехай
функція
![]() неперервна на відрізку
неперервна на відрізку![]() .
.
Тоді,
як було вказано вище, вона інтегровна
на відрізку
![]() ,
а значить і на відрізку
,
а значить і на відрізку![]() при будь-якому
при будь-якому![]() .
Розглянемо інтеграл
.
Розглянемо інтеграл
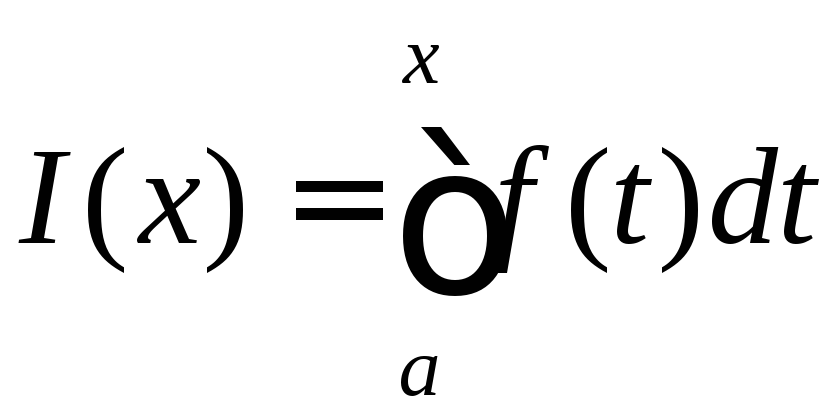 ,
,
![]() .
.
Тут
змінна інтегрування позначена
![]() ,
щоб не сплутати її з верхнью межею
,
щоб не сплутати її з верхнью межею![]() .
Кожному
.
Кожному![]() відповідає певне значення інтеграла
відповідає певне значення інтеграла
![]() ,
отже
,
отже
![]() є функція від
є функція від
![]() ,
задана на відрізку
,
задана на відрізку![]() .
Знайдемо похідну цієї функції.
.
Знайдемо похідну цієї функції.
Надамо
аргументу
![]() приріст
приріст![]() ,
тоді відповідний приріст
,
тоді відповідний приріст
![]() буде
буде
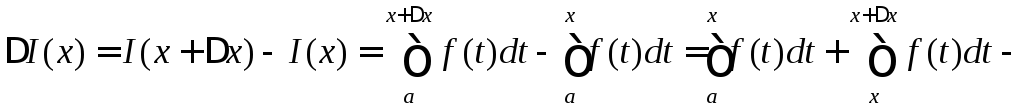
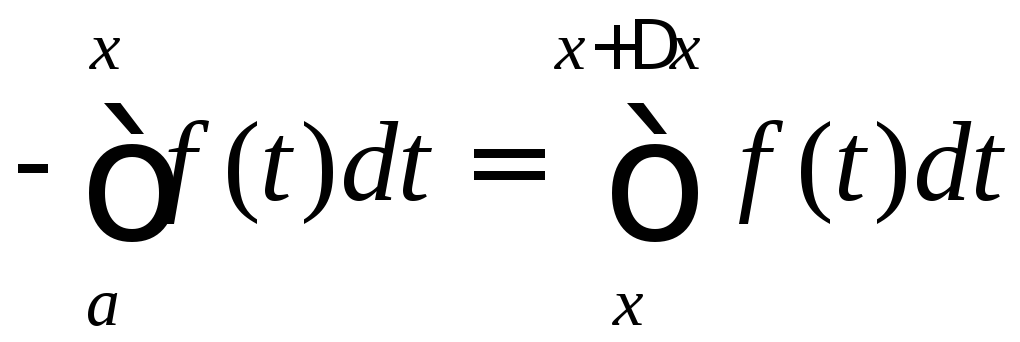
( тут ми скористалися з властивості адитивності визначеного інтеграла).
Далі застосуємо теорему про середнє значення
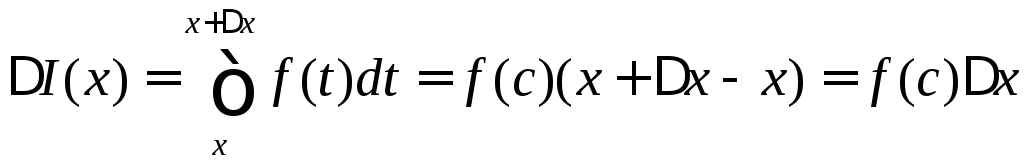 ,
,
де точка
![]() розташована поміж
розташована поміж![]() і
і![]() .
.
Згідно з означенням похідної
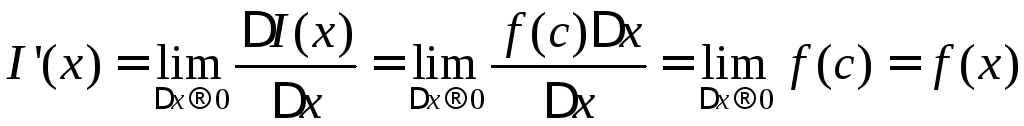 ,
тому що при
,
тому що при
![]() точка
точка![]() ,
а функція
,
а функція![]() неперервна.
неперервна.
Таким
чином встановлено дуже важливий факт:
похідна визначеного інтеграла по його
верхній межі дорівнює значенню
підінтегральної функції в точці, яка
дорівнює верхній межі, тобто
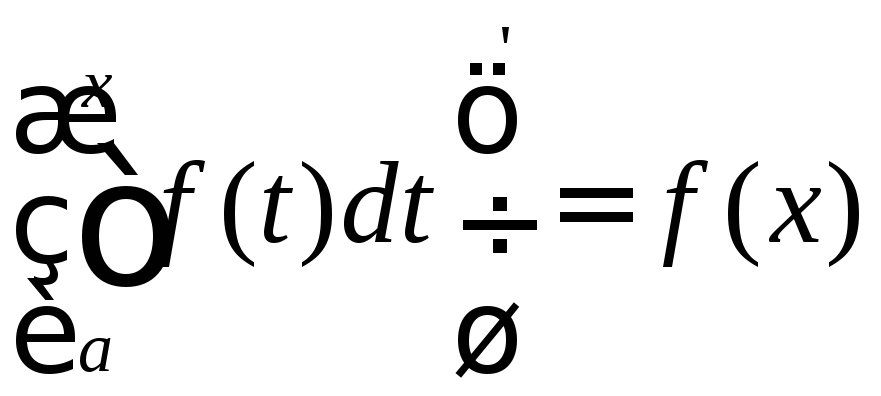 .
.
Це
означає, що будь-яка функція
![]() ,
неперервна на відрізку
,
неперервна на відрізку![]() ,
має на цьому відрізку первісну, при чому
інтеграл із змінною верхньою межею
,
має на цьому відрізку первісну, при чому
інтеграл із змінною верхньою межею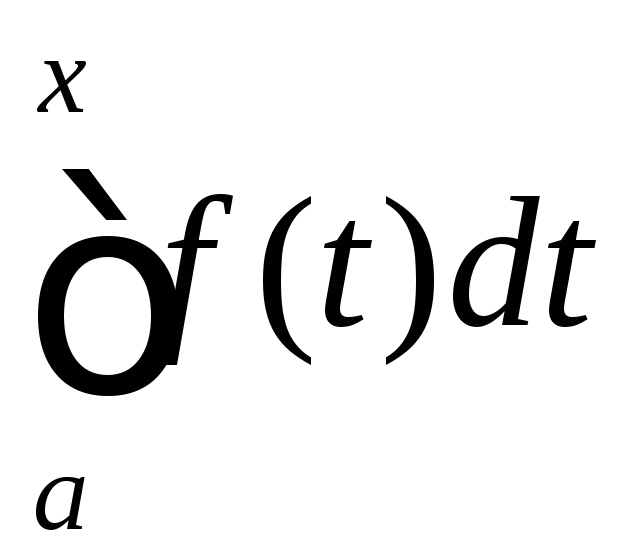 є первісною для
є первісною для![]() .
Цим встановлюється глибокий зв'язок
поміж невизначеним і визначеним
інтегралам, а саме
.
Цим встановлюється глибокий зв'язок
поміж невизначеним і визначеним
інтегралам, а саме
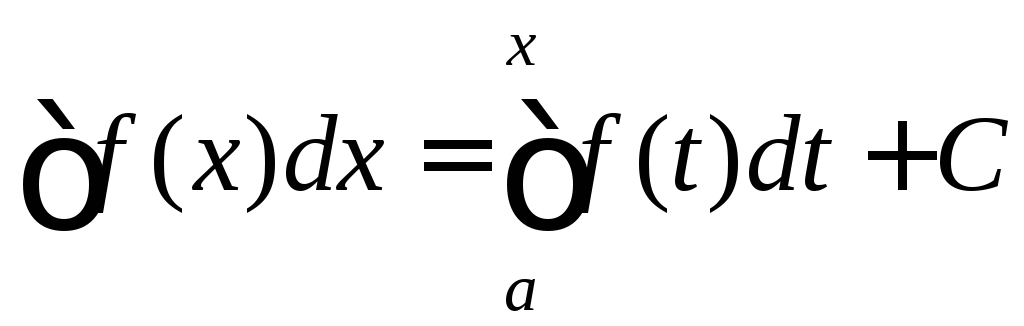 - де С
- довільна стала.
- де С
- довільна стала.
Нехай
тепер
![]() - яка-небудь первісна для функції
- яка-небудь первісна для функції![]() на відрізку
на відрізку![]() .
Дві первісні для однієї й тієї ж функції
відрізняються, як відомо, лише сталим
доданком. Тому
.
Дві первісні для однієї й тієї ж функції
відрізняються, як відомо, лише сталим
доданком. Тому
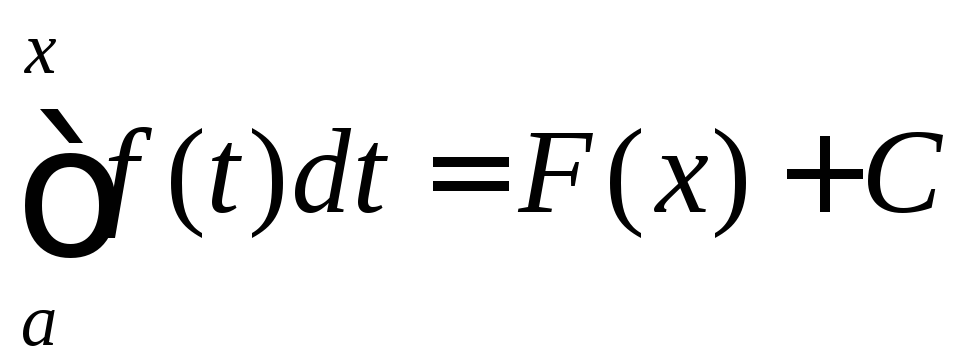 , де С –
деяка стала.
, де С –
деяка стала.
Покладемо
тут
![]() .
Тоді
.
Тоді
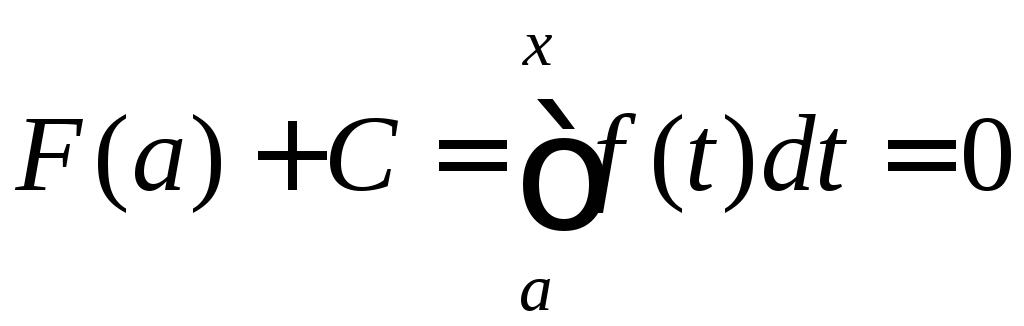 ,
звідки
,
звідки
![]() ,
так що
,
так що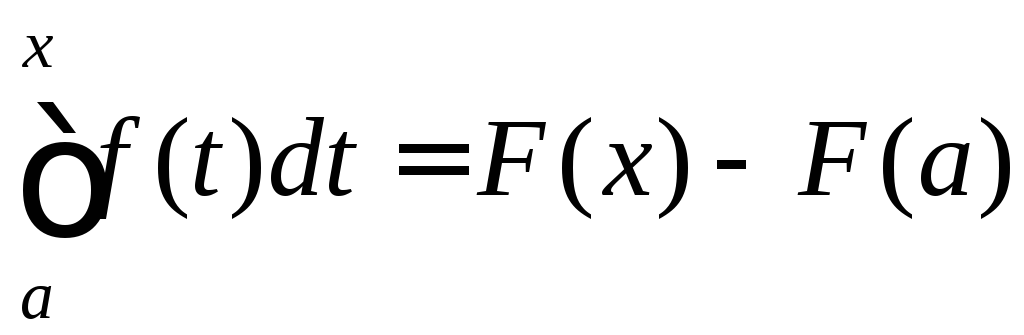 для будь-якого
для будь-якого![]() .
.
Покладаючи
тепер
![]() ,
отримуємо основну формулу інтегрального
числення
,
отримуємо основну формулу інтегрального
числення
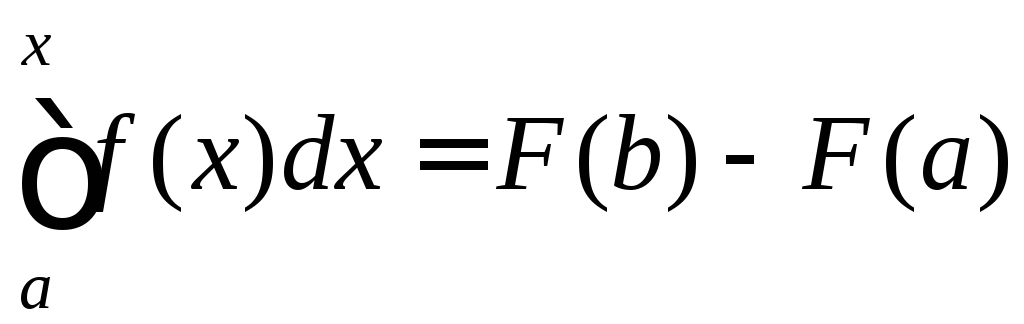 ,
,
яка називається формулою Ньютона-Лейбніца.
Отже,
визначений
інтеграл від неперервної функції
дорівнює приросту будь-якої її первісної
на всьому проміжку інтегрування. Зазвичай
користуються умовним позначенням:
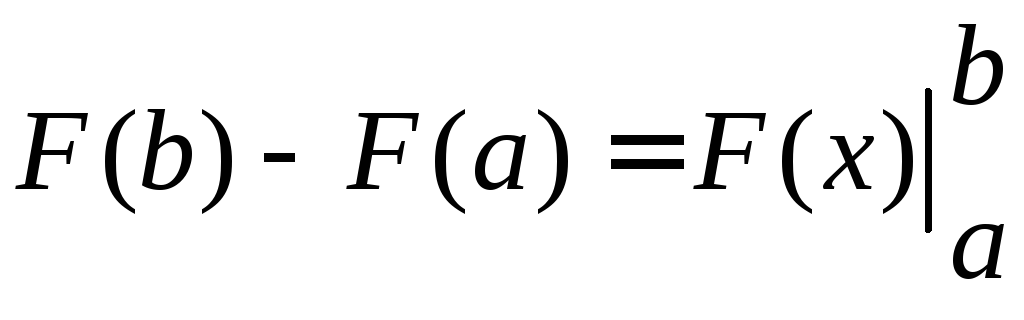 («
(«![]() з подвійною підстановкою від
з подвійною підстановкою від![]() до
до![]() »)
, і тоді формула Ньютона-Лейбніца
записується у вигляді
»)
, і тоді формула Ньютона-Лейбніца
записується у вигляді
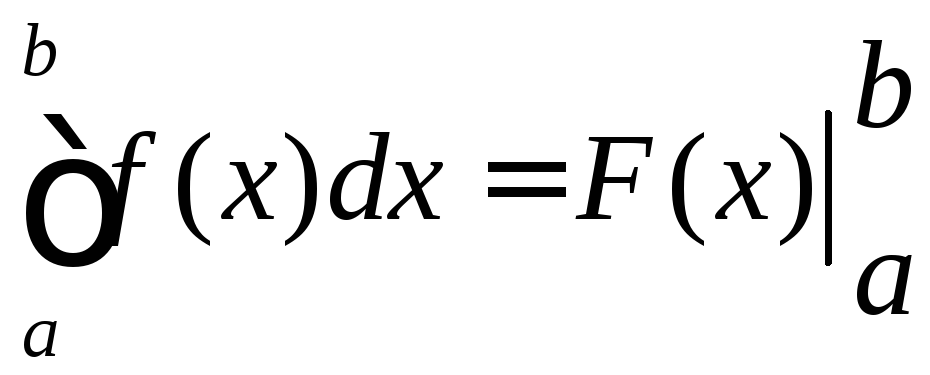 .
.
Ця формула відкриває великі можливості для обчислення визначених інтегралів, вона зводить задачу обчислення визначеного інтеграла до достатньо вивченої задачі відшукання невизначеного інтеграла.
Зазначимо, що при додержанні певних умов формула Ньютона-Лейбніца має місце і для розривних функцій.
Приклади.
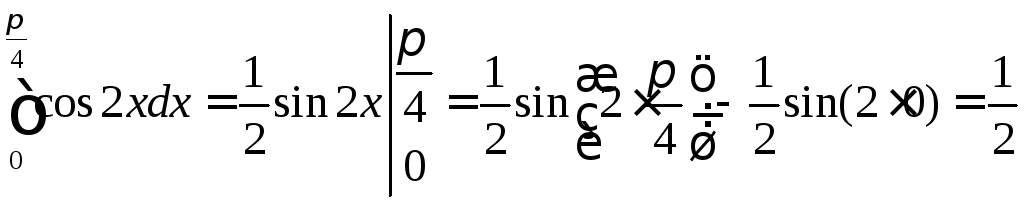 .
.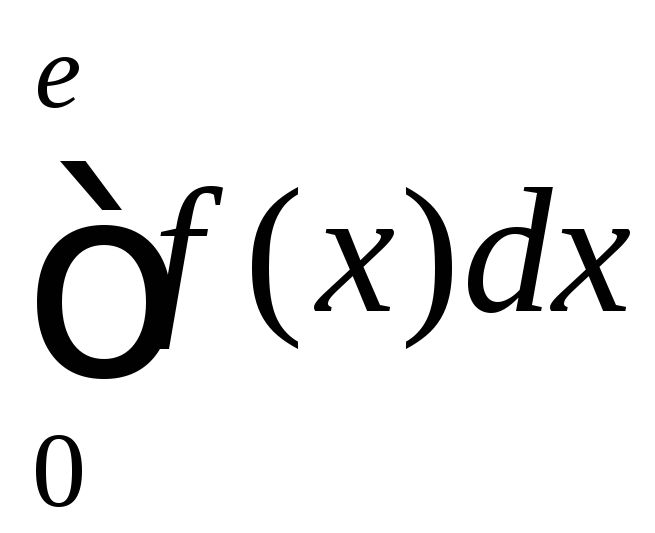 , де
, де
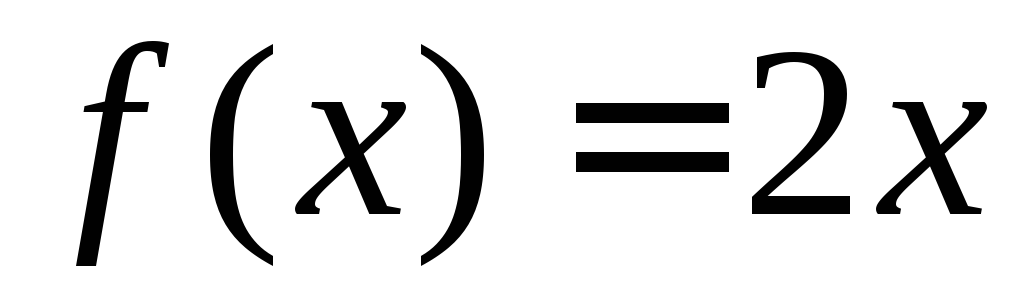 при
при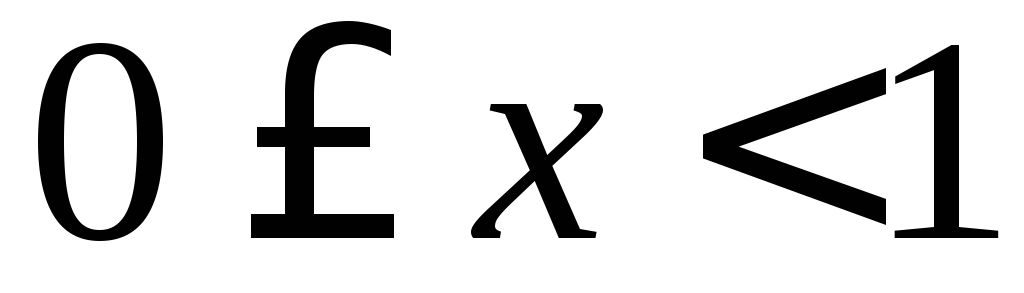 і
і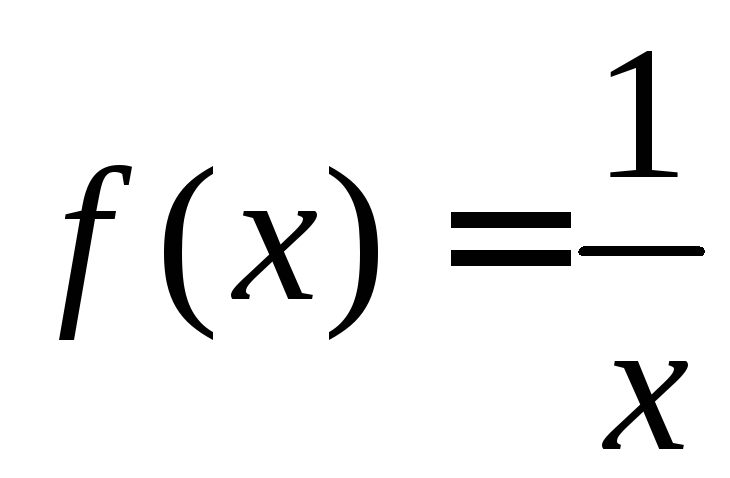 при
при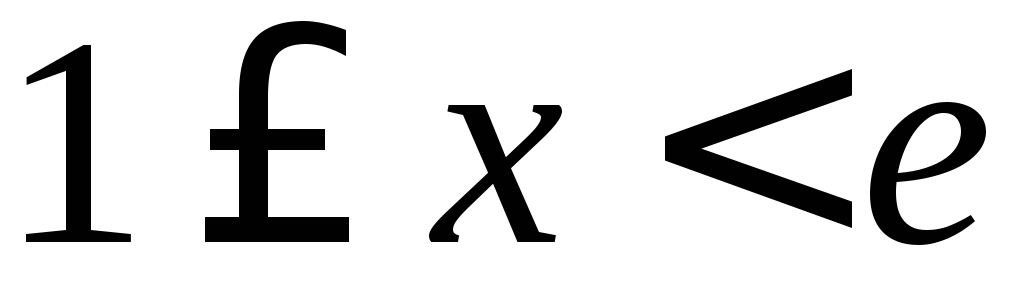 .
.
Тут
функція
![]() має розрив у точці
має розрив у точці![]() ,
але на кожному з проміжків
,
але на кожному з проміжків![]() і
і![]() вона неперервна. Скористаємося з
адитивності інтеграла:
вона неперервна. Скористаємося з
адитивності інтеграла:
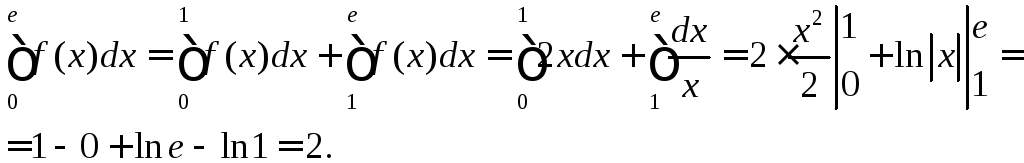
14. Метод заміни змінної у визначеному інтегралі
Теорема. Нехай
функція
 неперервна на відрізку
неперервна на відрізку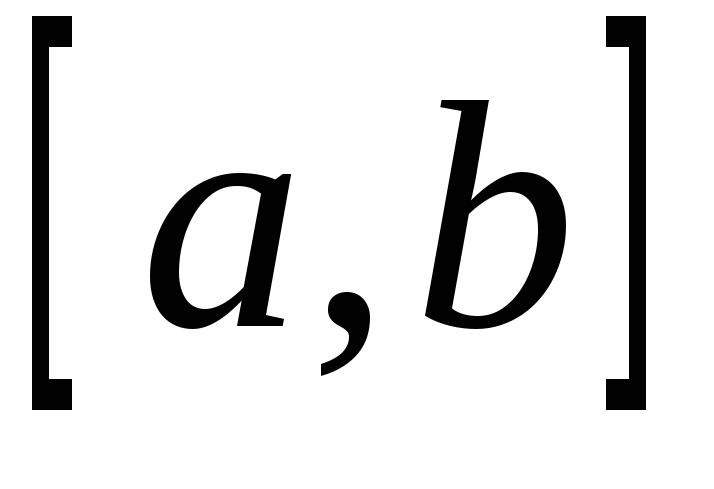 ;
;функція
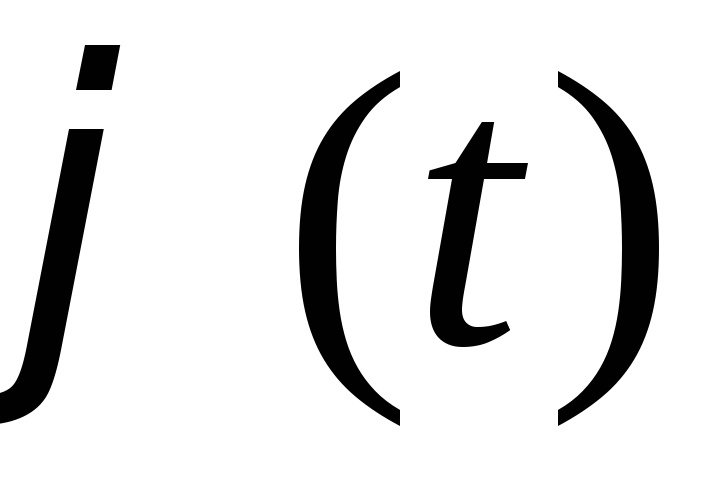 має неперервну похідну
має неперервну похідну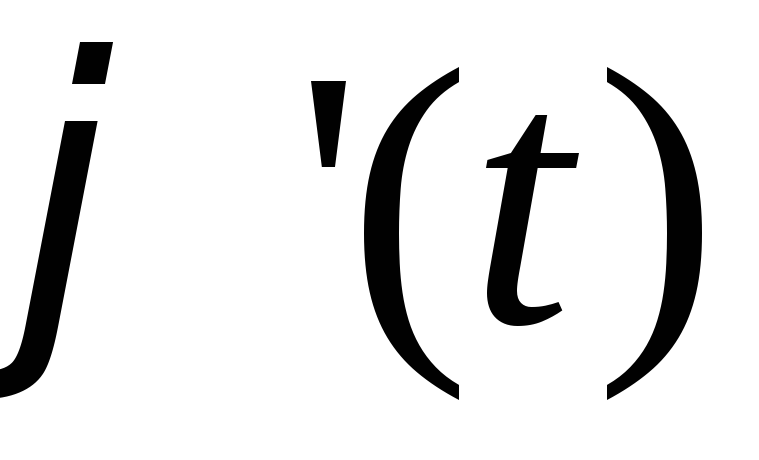 на відрізку
на відрізку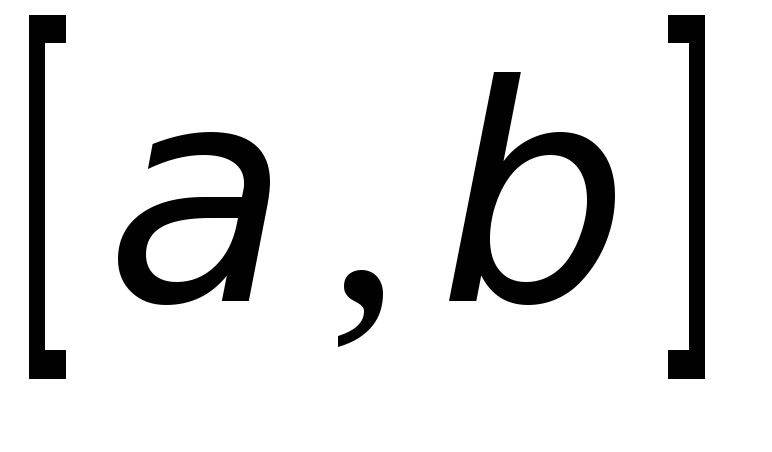 ;
;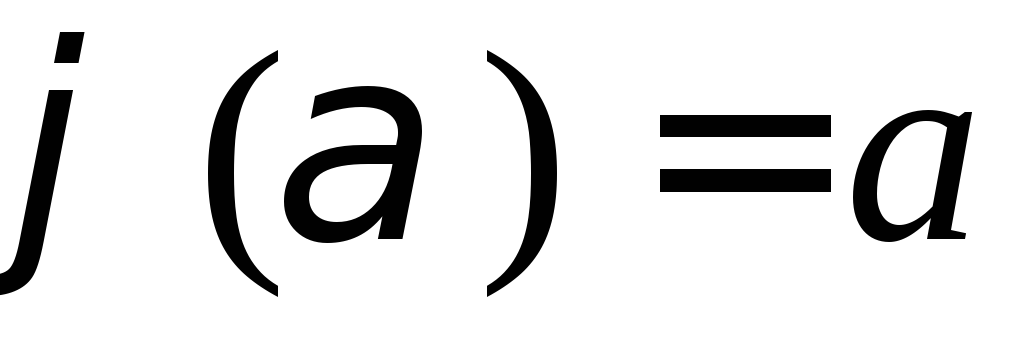 ,
,
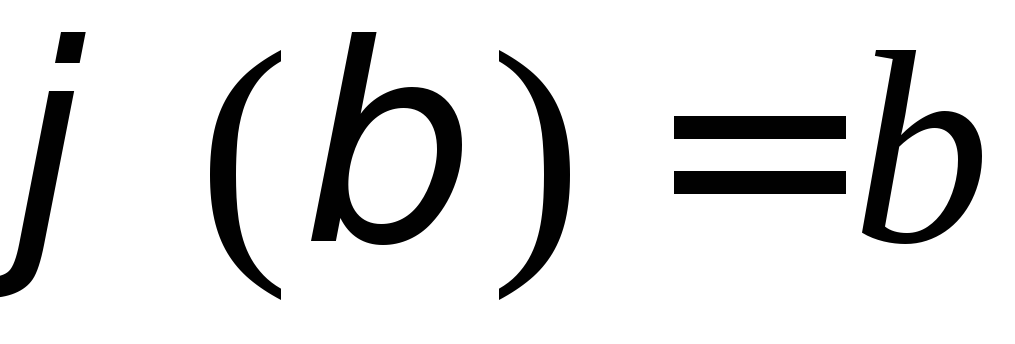 і для будь-якого
і для будь-якого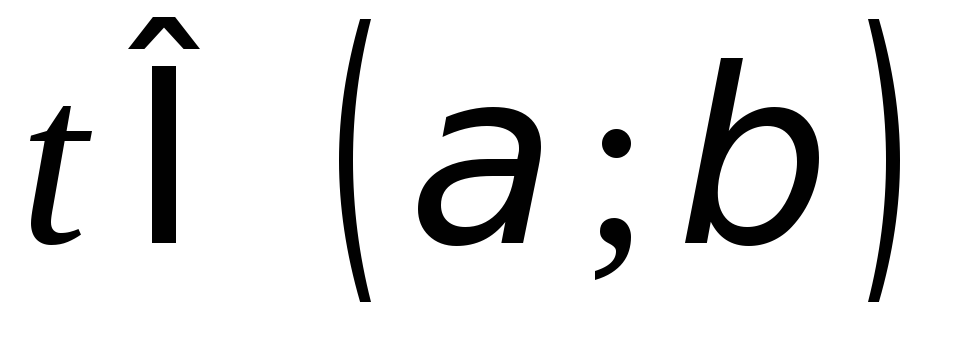 значення
значення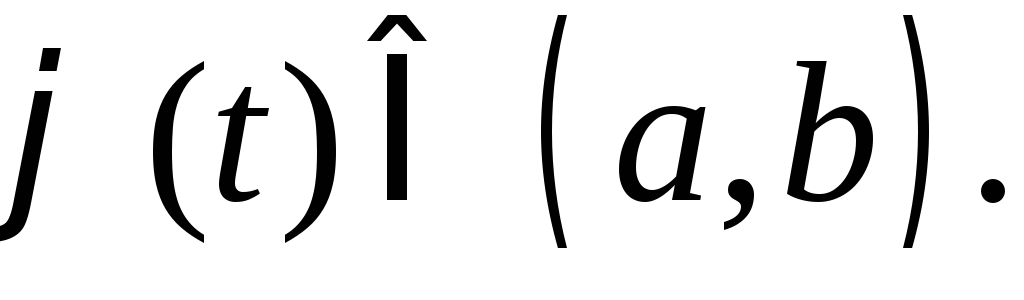
Тоді
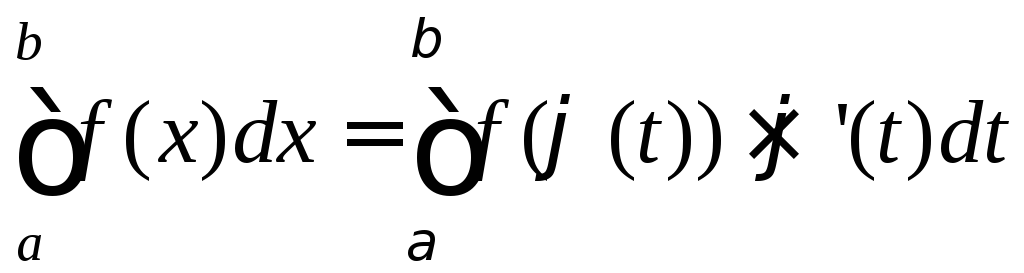 .
.
Оскільки
![]() неперервна на
неперервна на![]() , то вона має первісну, позначимо її
, то вона має первісну, позначимо її![]() .
Тоді функція
.
Тоді функція![]() буде первісною для функції
буде первісною для функції![]() на відрізку
на відрізку![]() (справді,
(справді,![]() ,
бо
,
бо![]() .
.
За формулою Ньютона-Лейбніца
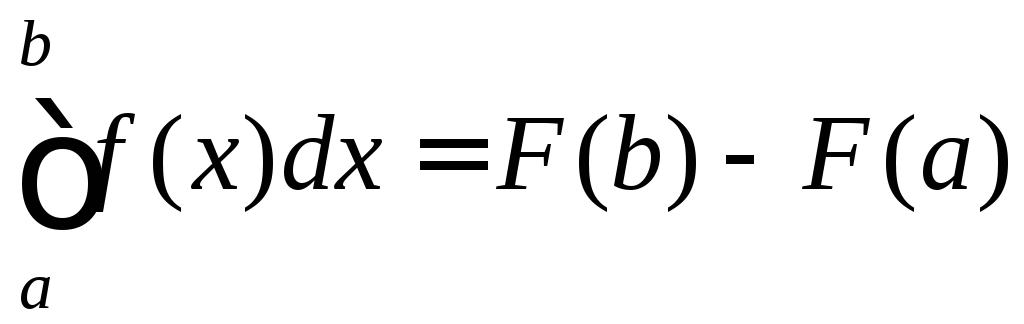
і
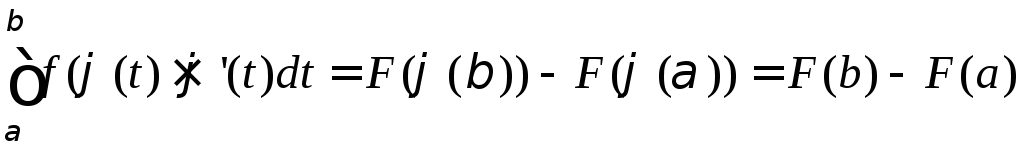 .
.
Отже
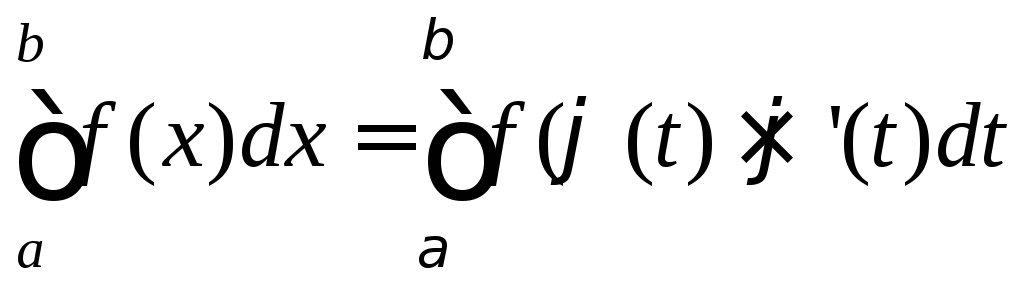 ,
що й треба було довести.
,
що й треба було довести.
Зауваження.
При заміні змінної у невизначеному
інтегралі необхідно було після
інтегрування повертатися до попередньої
змінної
![]() ,
але у визначеному інтегралі цього
робити не потрібно, натомість необхідно
встановити належним чином межі
інтегрування. Нові межі інтегрування
,
але у визначеному інтегралі цього
робити не потрібно, натомість необхідно
встановити належним чином межі
інтегрування. Нові межі інтегрування![]() і
і![]() відшукуються як розв’язки рівнянь
відшукуються як розв’язки рівнянь![]() і
і![]() відносно
відносно![]() і
і![]() .
.
Приклад.
Обчислити
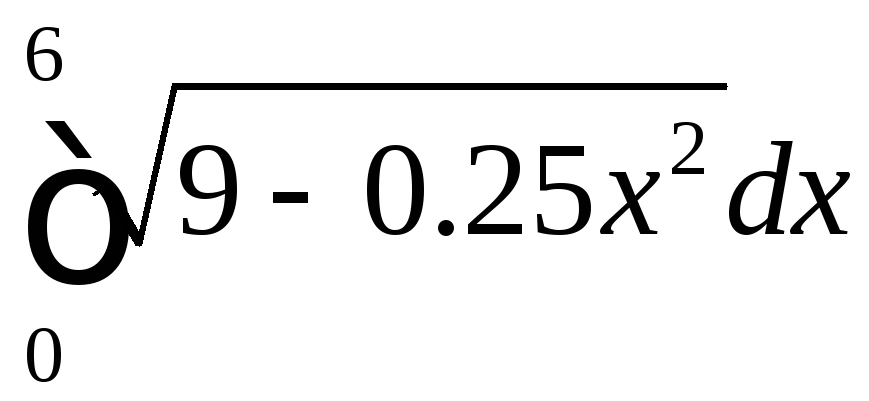 .
.
Розглянемо
підстановку
![]() .
Функція
.
Функція![]() неперервна на
неперервна на![]() ,
функція
,
функція![]() має неперервну похідну на відрізку
має неперервну похідну на відрізку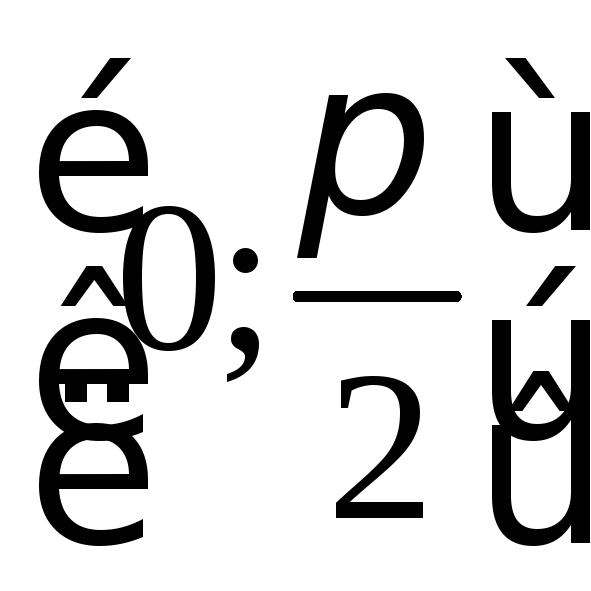 і при зміні
і при зміні![]() від
від![]() до
до![]() функція
функція![]() змінюється від
змінюється від![]() до
до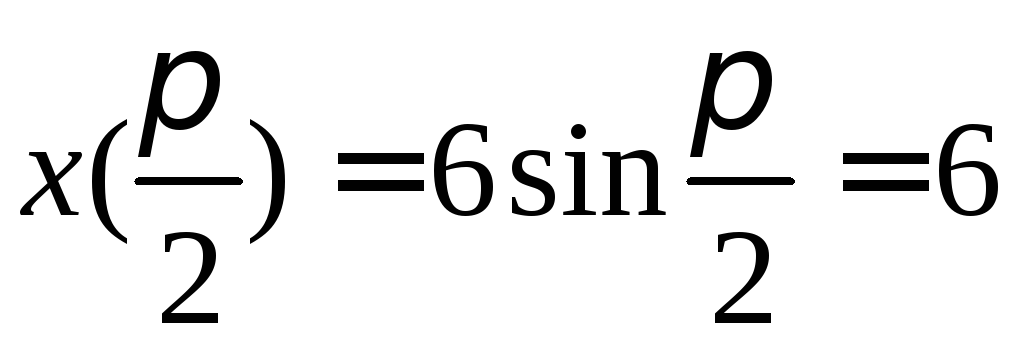 .
Отже всі умови теореми про заміну змінної
додержані.
.
Отже всі умови теореми про заміну змінної
додержані.