
- •Інтегральне числення функцій однієї змінної (конспект лекцій)
- •Таблиця інтегралів
- •Заміна змінної в невизначеному інтегралі (метод підстановки)
- •4.Інтегрування частинами у невизначеному інтегралі
- •Інтегрування раціональних функцій
- •Інтегрування деяких ірраціональних функцій
- •7. Інтегрування деяких виразів, що містять тригонометричні функції
- •8. Використання таблиць інтегралів
- •9. Поняття про інтеграли, що не виражаються через елементарні функції
- •10. Приклади задач, що приводять до поняття визначеного інтеграла
- •2)Задача про шлях точки у прямолінійному русі.
- •11. Означення визначеного інтеграла
- •12. Основні властивості визначеного інтеграла
- •13. Інтеграл як функція верхньої межі. Формула Ньютона-Лейбніца
- •14. Метод заміни змінної у визначеному інтегралі
- •15. Інтегрування частинами у визначеному інтегралі
- •16. Загальна схема застосування визначеного інтеграла
- •17. Обчислення площі плоскої фігури
- •18. Обчислення довжини дуги
- •19. Обчислення об’єму тіла
- •20. Обчислення площі бічної поверхні тіла обертання
- •21. Обчислення роботи змінної сили
- •22. Обчислення сили тиску рідини на вертикальну пластину
- •23. Невластивий інтеграл по нескінченному проміжку
- •24. Ознаки збіжності невластивого інтеграла по нескінченному проміжку
- •25. Невластивий інтеграл від необмеженої функції
- •26. Ознаки збіжності невластивого інтеграла від необмеженої функції
- •27. Наближене обчислення визначених інтегралів
Інтегральне числення функцій однієї змінної (конспект лекцій)
![]()
Первісна функція. Невизначений інтеграл та його властивості
В
диференціальному численні основним
завданням було відшукання похідної
заданої функції. Але в багатьох питаннях
математичного аналізу і його застосувань
виникає потреба розв’язати
обернену задачу: За даною функцією
![]() знайти таку функцію
знайти таку функцію![]() ,
похідна якої дорівнювала б
,
похідна якої дорівнювала б![]() ,
тобто
,
тобто![]() .
.
Приклад.
У диференціальному численні було
показано, що миттєва швидкість
прямолінійного руху точки дорівнює
похідній координати точки:
![]() .
Але якщо за заданою швидкістю руху точки
.
Але якщо за заданою швидкістю руху точки![]() потрібно визначити закон її руху, тобто
залежність її координати від часу
потрібно визначити закон її руху, тобто
залежність її координати від часу![]() , то це і означає, що треба знайти таку
функцію
, то це і означає, що треба знайти таку
функцію![]() ,
похідна якої дорівнює заданій функції
,
похідна якої дорівнює заданій функції![]() .
.![]()
Означення.
Функція
![]()
![]() називається первісною
для функції
називається первісною
для функції
![]() на деякому проміжку
на деякому проміжку
![]() ,
якщо для всіх значень
,
якщо для всіх значень
![]() виконується рівність
виконується рівність
![]() .
.
Приклад.
Функція
![]() є первісною для функції
є первісною для функції
![]() на всій числовій осі, бо при будь-якому
значенні
на всій числовій осі, бо при будь-якому
значенні
![]() буде
буде
![]()
![]() .
.
Зазначимо,
що функції
![]() ,
,
![]() і взагалі
і взагалі![]() ,
де
,
де![]() будь-яка стала, також є первісними для
будь-яка стала, також є первісними для
![]() .
.
Розглянутий
приклад свідчить, що первісна
![]() для даної функції
для даної функції
![]()
![]() визначається неоднозначно. Справді,
очевидно, що якщо
визначається неоднозначно. Справді,
очевидно, що якщо
![]() ,
то і
,
то і
![]() ,
тобто
,
тобто![]() при будь-якій сталій
при будь-якій сталій![]() також є первісною для функції
також є первісною для функції![]() .
Виникає питання: чи вичерпує множина
функцій вигляду
.
Виникає питання: чи вичерпує множина
функцій вигляду![]()
![]() усю сукупність первісних для функції
усю сукупність первісних для функції
![]() ?
Виявляється, що так.
?
Виявляється, що так.
Теорема.
Якщо
![]() - первісна для функції
- первісна для функції
![]() на деякому проміжку
на деякому проміжку
![]() ,
то будь-яка інша первісна для
,
то будь-яка інша первісна для
![]() на тому ж проміжку може буди подана у
вигляді
на тому ж проміжку може буди подана у
вигляді
![]() ,
де
,
де
![]() –
стала.
–
стала.
Нехай
![]() - яка небудь інша первісна для
- яка небудь інша первісна для
![]() на
на
![]() ,
тобто
,
тобто
![]() ,
,
![]() .
Позначимо
.
Позначимо
![]() .
Тоді для будь-якого
.
Тоді для будь-якого
![]() :
:
![]() .
.
Як
відомо з диференціального числення, це
означає, що
![]() ,
отже
,
отже
![]() або
або
![]() .
Означення.
Множина всіх первісних для даної функції
.
Означення.
Множина всіх первісних для даної функції
![]() на проміжку
на проміжку![]() називаєтьсяневизначеним
інтегралом
від функції
називаєтьсяневизначеним
інтегралом
від функції
![]() на цьому проміжку і позначається
на цьому проміжку і позначається![]() (
(![]() називається підінтегральною функцією,
називається підінтегральною функцією,![]()
![]() - підінтегральним виразом, а
- підінтегральним виразом, а![]() - змінною інтегрування).
- змінною інтегрування).
Згідно
з вищезазначеним
![]() =
=![]() , де
, де
![]() - яка небудь
первісна для функції
- яка небудь
первісна для функції
![]() ,
а
,
а
![]() –
довільна стала.
–
довільна стала.
Відзначимо основні властивості невизначеного інтеграла.
Похідна невизначеного інтеграла дорівнює підінтегральній функції:

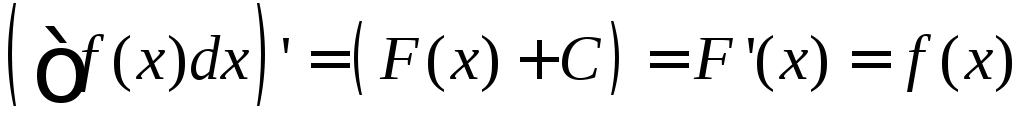 .
.Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу:
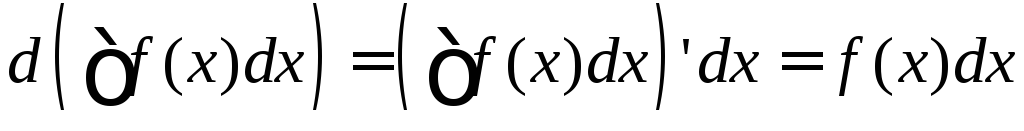 .
.Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої:
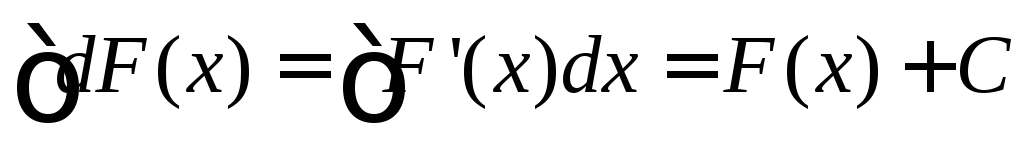 .
.
Перелічені властивості показують, що інтегрування і диференціювання
– взаємно обернені операції.
Сталий множник можна виносити за знак інтеграла:
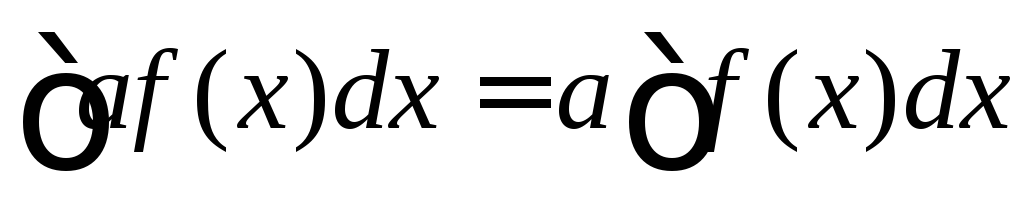 ,
якщо
,
якщо
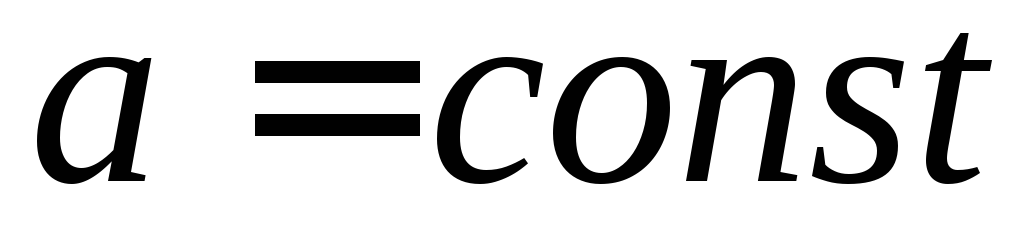 .
.Невизначений інтеграл від алгебраїчної суми скінченного числа функцій дорівнює алгебраїчній сумі інтегралів від доданків. Наприклад
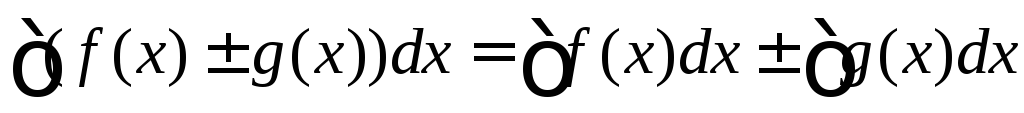 .
.
Властивості 4) і 5) перевіряються почленним диференціюванням відповідних рівностей на підставі 1) .
Таблиця інтегралів
У наведеній нижче таблиці основних інтегралів частина формул безпосередньо випливає з таблиці похідних і визначення інтегрування як дії, оберненої до диференціювання, інші перевіряються диференціюванням. Цю таблицю необхідно вивчити, оскільки існуючі методи інтегрування якраз мають метою звести шуканий інтеграл до табличних.
1)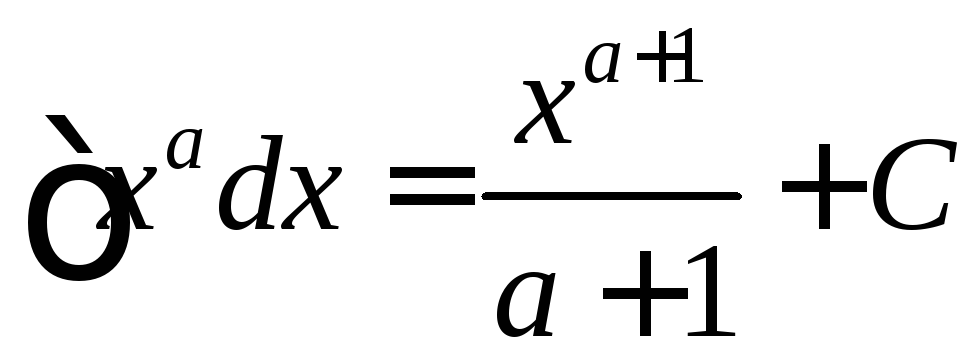 ,
,![]()
2)
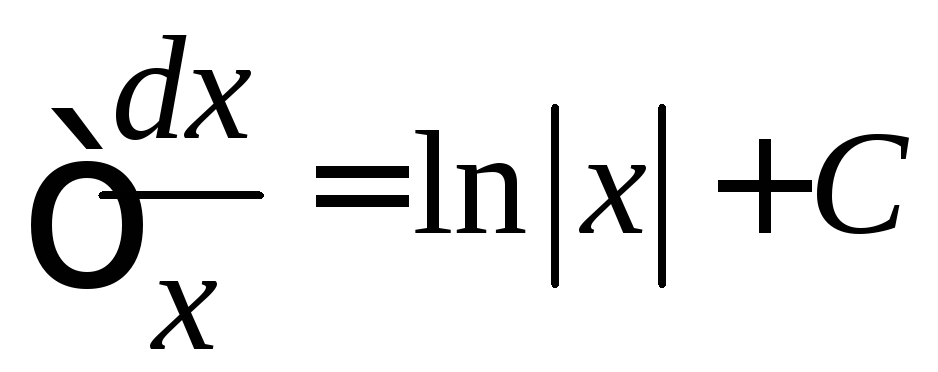 ,
,
3)
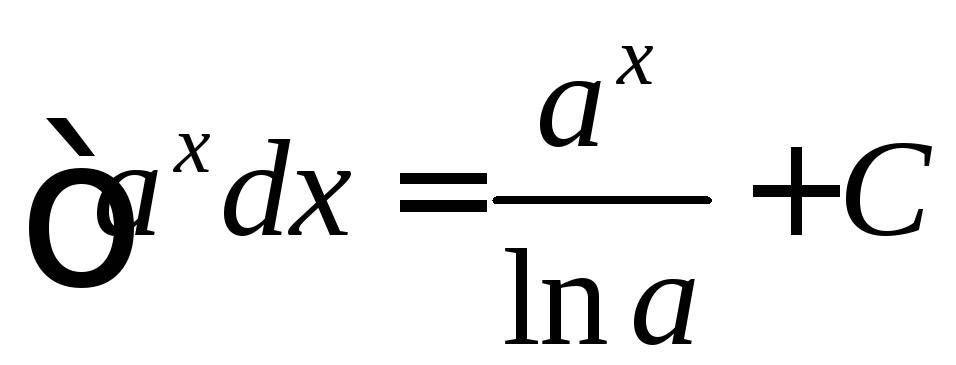 ,
зокрема
,
зокрема
![]() ,
,
4)![]() ,
,
5)
![]() ,
,
6)
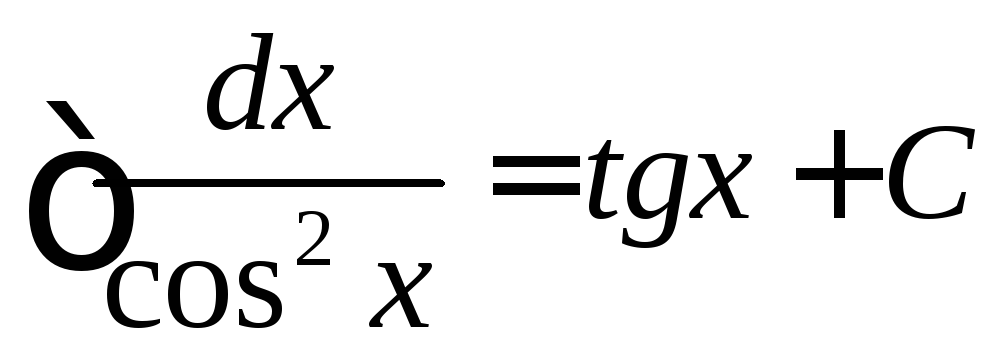 ,
,
7)
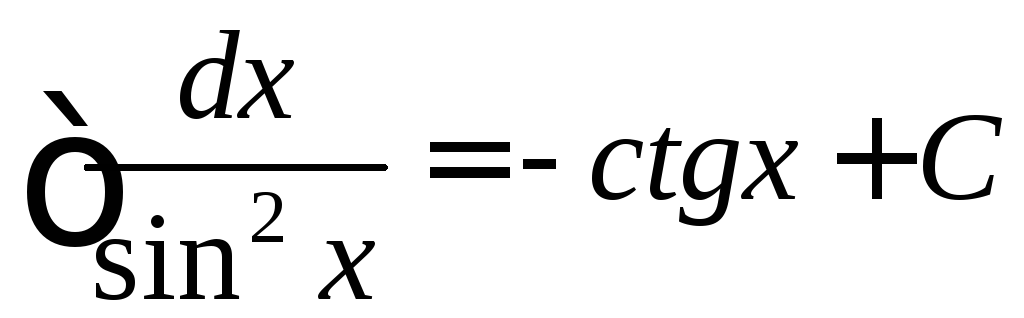 ,
,
8)
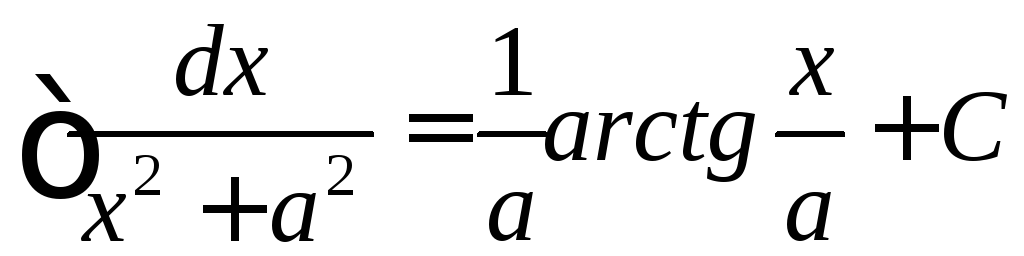 ,
,
9)
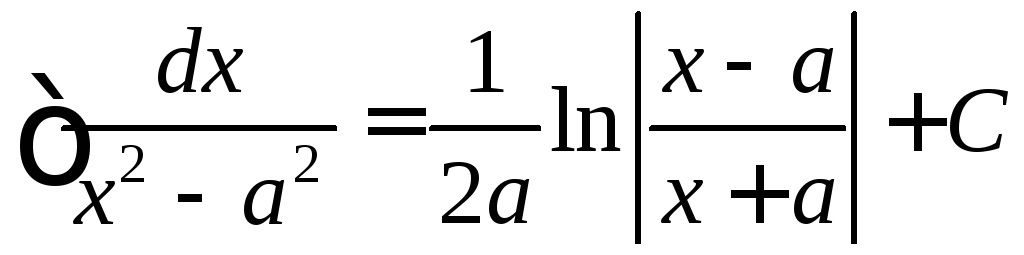 ,
,
10)
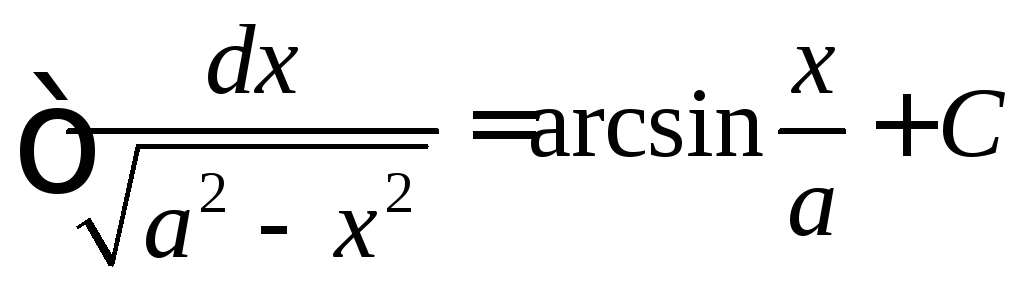 ,
,
11)
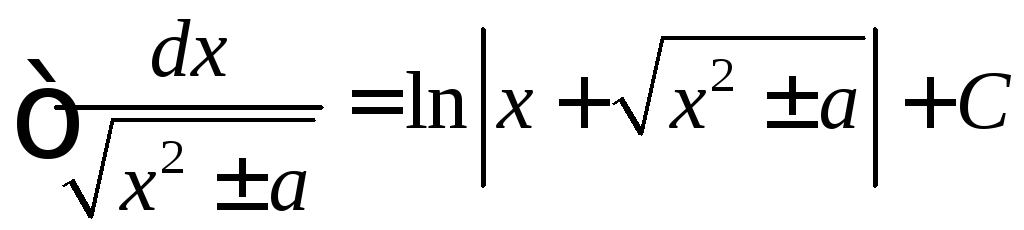 .
.
Основні властивості невизначеного інтеграла разом з наведеною тут таблицею інтегралів уже дозволяють знаходити деякі інтеграли (метод безпосереднього інтегрування).
Приклад. Знайти інтеграли
а)
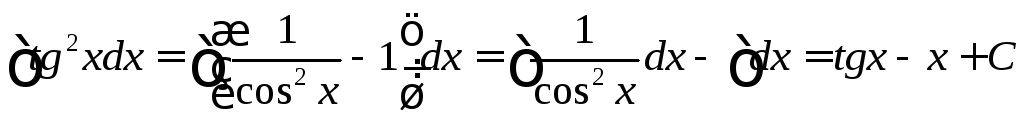 .
.
б)
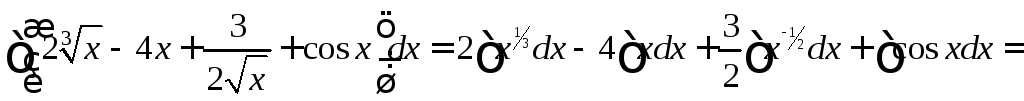
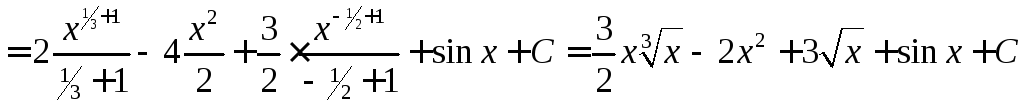 .
.
