Применяем к последнему выражению неравенство Коши – Буняковского.

Теорема 3. Если{xk }, k=1,2,…n ортогональная система ненулевых элементов в евклидовом пространстве E , xk E , то элементы линейно независимы.

Для линейно независимых векторов {xk } , k =1,2,…n равенство

выполняется только в одном случае, когда все коэффициенты равны нулю.

ak 0, k 1,2, n

22

Следствие. В n – мерном евклидовом пространстве ортогональная система из n ненулевых элементов образует

базис.

Если система векторов {xk } , k=1,2,…n в ЛП E образует базис, то любой другой вектор этого пространства y E можно представить в виде линейной комбинации векторов базиса.

23

Гильбертово пространство

Пространством Гильберта называется евклидово пространство, которое полно с нормой.

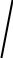x x, x

Пример. Пространство арифметических векторов со

скалярным произведением, определенным для векторов x, y E n как

является полным пространством, т.е. гильбертовым пространством.

24

Пример. Пространство L2 [a, b] кусочно-непрерывных на отрезке t[a,b] функций со скалярным произведением и нормой

a

гильбертово.

Замечание. Если требование кусочной непрерывности заменить на непрерывность функций, то полученное пространство не будет полным, а значит, не будет гильбертовым.

25

Аппроксимация в гильбертовом пространстве

Сформулируем задачу аппроксимации. Пусть H - гильбертово пространство, а L - подпространство L H . Для произвольного элемента x H необходимо найти элемент наилучшего приближения (ЭНП) y L , для которого (x, y) = (x, L), то есть

Теорема 4. Существует единственный ЭНП , который является решением задачи аппроксимации.

26

Теорема 5. Пусть L - подпространство в гильбертовом пространства H , пусть y L - ЭНП для элемента x H . Тогда любой элемент u L ортогонален элементу v=x-y : v u , что обозначают также v L .

Следствие из теорем 4, 5. Пусть L - подпространство в H . Тогда x H существует единственное разложение x=y+z , где y L - ЭНП, а z L . В силу единственности элемента y элемент z=x-y также единственный.

Элемент наилучшего приближения (ЭНП) y L называют проекцией элемента x H на пространство L (вспомните пример с трехмерным декартовым пространством).

27

Теорема 5 дает способ нахождения ЭНП для x H в случае конечной размерности подпространства L с заданным базисом

Алгоритм поиска коэффициентов следующий. Так как любой элемент {gk } перпендикулярен x-y , имеем

k : gk L, x y, gk 0

Заменяем y суммой и поучаем:

28

Перепишем эти соотношения в виде системы уравнений.

n

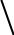
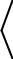j g j , gk x, gk 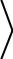, k 1, , n

j 1

Матрица коэффициентов этой системы называется матрицей Грама

В силу линейной независимости элементов {g1, g2 ,...gn} определитель этой матрицы отличен от нуля.

det G 0

29

Так как определитель системы уравнений отличен от нуля, эта система имеет единственное решение.

1, 2 , , n

Задача поиска коэффициентов { k }значительно упрощается, если элементы базиса {g1, g2 ,...gn} не только линейно независимы, но и еще ортогональны. В этом случае можно обойтись без решения системы уравнений, а сразу написать аналитические выражения для коэффициентов.