Упражнения

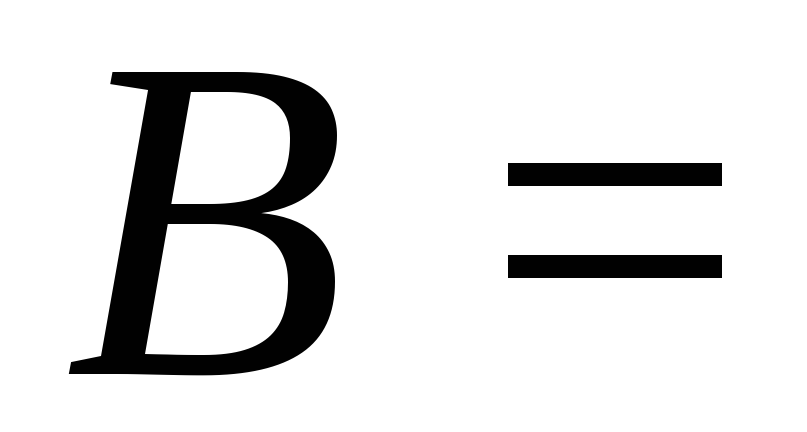1. Пусть {2, 3};{3, 4};{1, 0}. Найти:

1) ;	6) ;
2) ;	7) ;
3) ;	8) ;
4) ;	9) ;
5) ;	10) .

2. Определить мощности множеств ;;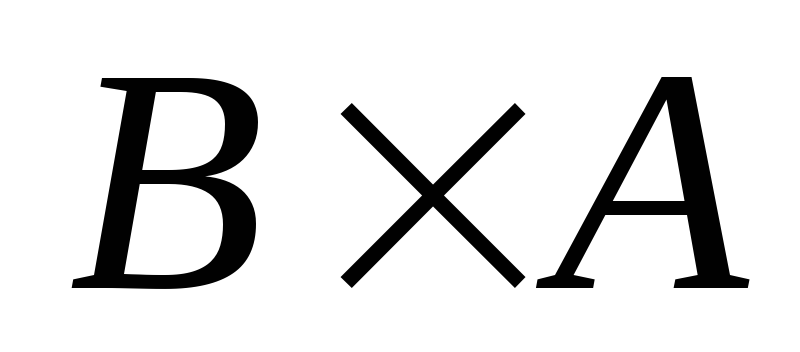_{; ; ; , и построить их, если}

1) ;; 3);;

2) = {(1; 2)},= {a; b; c; d}; 4) = {1; 2; 3},= {1; 2}.

3. Записать все слова из 3-х букв, которые можно построить из алфавита А. Осуществить перечисление в лексикографическом порядке.

1); 2); 3)

4. Пусть _{; ; и . Описать и изобразить графически следующие множества}

1) ; 3)_;

₂₎ ; 4)

5. Найт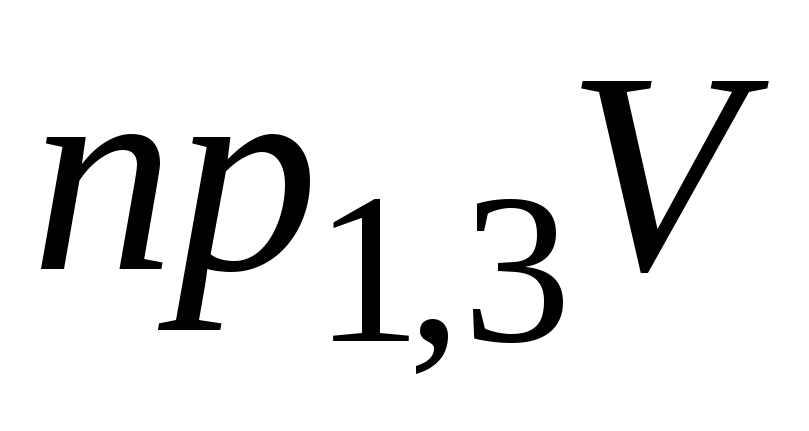и ;;_{; ; ;} , если

1) ;

2) ;

3) ;

4) .

1.3. Комбинаторика Правило суммы

Классическая формулировка

Если элемент можно выбратьk способами, а элемент можно выбратьm способами. Тогда или можно выбратьk +m способами.

Современная формулировка (теорема о мощности объединения множеств)

Количество элементов объединения двух множеств равно сумме количества элементов в первом и во втором множестве, за вычетом количества элементов их пересечения:

.

Причем, если множества не пересекаются, то теорема приобретает вид, аналогичный классической формулировке:

.

Для трех множеств теорема имеет вид:

.

Общее правило для имеет вид::

Правило произведения

Классическая формулировка

Если элемент можно выбратьk способами, а элемент можно выбратьm способами. Тогда и можно выбратьkm способами.

Современная формулировка (теорема о мощности прямого произведения множеств)

Количество элементов прямого произведения двух множеств равно произведению количества элементов первого и второго множества:

.

Пример. Из 3 экземпляров учебника алгебры, 7 экземпляров учебника геометрии и 6 экземпляров учебника физики, надо выбрать комплект, содержащий все учебники по одному разу. Сколькими способами это можно сделать?

Множество А – учебники по алгебре, В – учебники по геометрии, С – по физике. Надо составить и пересчитать все тройки из множества .

Число размещений без повторений

Число размещений без повторений из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k различными координатами.

Число размещений без повторений находится по формуле:

.

Пример: Сколькими способами можно построить 3-значное число с различными цифрами, не содержащее цифры 0?

Количество цифр , размерность вектора с различными координатами

Число размещений с повторениями

Число размещений с повторениями из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k координатами, среди которых могут быть одинаковые.

Число размещений с повторениями находится по формуле:

.

Пример: Сколько слов длины 6 можно составить из 26 букв латинского алфавита?

Количество букв , размерность вектора

Число перестановок без повторений

Число перестановок без повторений из n элементов – это число способов, сколькими можно расположить на n различных местах n различных элементов.

Число перестановок без повторений находится по формуле:

.

Замечание: Мощность искомого множества А удобно искать по формуле: , гдех – число способов выбрать нужные места; у – число способов расположить на них нужные элементы; z – число способов расположить остальные элементы на оставшихся местах.

Пример. Сколькими способами можно расставить на книжной полке 5 различных книг? В скольких случаях две определенные книги А и В окажутся рядом?

Всего способов расставить 5 книг на 5-ти местах – равно = 5! = 120.

В задаче х – число способов выбрать два места рядом, х = 4; у – число способов расположить две книги на двух местах, у = 2! = 2; z – число способов расположить остальные 3 книги на оставшихся 3-х местах,  z = 3! = 6. Значит = 48.