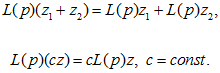Глава 2

Уравнение n-го порядка для одной неизвестной функции z независимого переменного t с постоянными коэффициентами имеет вид:

где a₁,¼,a_n - постоянные числа (действительные или комплексные). К уравнению (2.1), очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось. (См. соответствующую формулировку в первом параграфе первой главы). Решения уравнения (2.1) будут построены в явном виде и тем самым установлена еще раз теорема существования. Теорема единственности будет использоваться по существу для доказательства того, что найдены все решения данного уравнения.

Прежде, чем приступить к решению уравнения (2.1) условимся о некоторых обозначениях и понятиях.

Производную по времени от произвольной функции z = z(t) удобно обозначать через pz = p(z), трактуя символ p как линейную операцию над функцией z:

Тогда натуральная степень k операции p, обозначаемая через p^k, естественно понимается как и представляет собой производнуюk-го порядка от функции z:

Ясно, что степень p^k операции p подчиняется формальным алгебраическим правилам

Естественным представляется определение операции cp^k, где c - число и суммы p^k + p^m:

Пользуясь введенными обозначениями, мы можем записать левую часть уравнения (2.1) в виде

Положим

Данное выражение в соответствии с равенством (2.5) представляет собой линейную операцию над функцией z, т.е.

С другой стороны само выражение (2.6) представляет собой выражение относительно символа p с постоянными (действительными или комплексными) коэффициентами, для которого справедливы обычные алгебраические правила оперирования, т.е. если L(p) и M(p) - два произвольных многочлена относительно символа p (или, как говорят, оператора дифференцирования p), то

Предложение 2.1.1 Если L(p) -многочлен относительно оператора дифференцирования вида (2.6), то справедлива следующая формула

Здесь l - произвольное действительное или комплексное число;

Доказательство. Мы имеем

Отсюда следует, что и поэтому справедлива формула(2.8).

Из формулы (2.8) следует, что функция e^lt является решением уравнения (2.1), т.е.

тогда и только тогда, когда число l есть корень многочлена L(l), т.е.

Многочлен L(l) называется характеристическим многочленом уравнения (2.1), а уравнение (2.9) - характеристическим уравнением.

Совокупность всех решений уравнений (2.1) описывается несколько по разному в зависимости от того имеет ли кратные корни характеристическое уравнение (2.9), либо корни простые. Рассмотрим отдельно эти случаи.