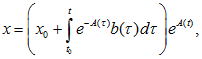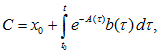8.Уравнения с разделяющимися переменными

Так называются уравнения

(1.27)

Рассматриваемое уравнение есть уравнение в полных дифференциалах

Теорема

Пусть функции f(t) и g(t)

непрерывны причем g(x) нигде не обращается в ноль, где a < t < b, c < x < d.

Тогда через каждую точку (t₀,x₀ ) прямоугольника Q: {(t, x), a < t < b, c < x < d} проходит одно и только одно решение д. у. (1.27)

Замечание: чтобы решить данное уравнение (1.27) нужно разделить переменные и проинтегрировать

∫dx/g(x) =∫f(t)dt Если g(x*) = 0 в точке x = x*, то x = x* является решением

(1.27)

9.Однородные уравнения первого порядка

Уравнение первого порядка

называется однородным, если f(t,x) есть однородная функция своих аргументов нулевой степени однородности, т.е. имеет место тождество

(1.28)

однородное уравнение всегда можно представить в виде

(1.29)

Будем предполагать, что функция h(y) определена и непрерывна на интервале a₁ < y < b₁ и что на этом интервале функция h(y) - y в нуль не обращается.

Уравнение (1.29) решается посредством замены переменных. Точнее, вместо неизвестной функции x(t) введем новую неизвестную функцию y(t):

Произведя такую подстановку, для новой неизвестной функции y получаем уравнение

(1.30)

Мы получили уравнение с разделяющимися переменными

10.Линейные уравнения первого порядка

Линейным уравнением первого порядка называют уравнения

(1.20)

где a(t), b(t) - заданные функции переменной t.

Теорема

Пусть функции a(t) и b(t) определены и непрерывны на некотором интервале a < t < b тогда через точку (t₀,x₀). Проходит одна и только одна интегральная кривая д.у. определенная при всех t принадлежащих (a,b). Пусть t₀ - некоторая точка интервала (a,b). Положим

(1.21)

Функция A(t), очевидно, определена на интервале a < t < b. Докажем, что совокупность всех решений уравнения (1.20) задается формулой

(1.22)

где x₀ - произвольная константа. Для вывода формулы (1.22) рассмотрим сначала однородное уравнение, соответствующее (1.20), т.е. уравнение

(1.23)

Это уравнение в полных дифференциалах. В самом деле, символически его можно записать в виде

Соответствующая функция F(t,x) легко вычисляется:

где A(t) определена по формуле (1.21). В таком случае, согласно вышесказанному, решения уравнения (1.23) определяются как неявные функции из соотношения

Отсюда находим или

(1.24)

где C может принимать любые действительные значения.

Для получения с помощью формулы (1.24) решения неоднородного уравнения (1.20) применяется так называемый 11.метод вариации постоянной. То есть решение уравнения (1.20) ищется в виде (1.24), но C уже не константа, а некоторая неизвестная функция переменного t. Подставляя выражение

(1.25)

в уравнение (1.20), получим:

или, что то же

Отсюда находим

(1.26)

где x₀ - константа интегрирования. На основании (1.25), (1.26) получаем формулу (1.22).

Некоторые дифференциальные уравнения путем замены переменных могут быть сведены к линейным. К таким уравнениям относится так называемое уравнение Бернулли, имеющее вид

Это уравнение заменой переменной сводится к линейному. Действительно, так как

то произведя подстановку, получим линейное уравнение

Рассмотрим уравнение Риккати:

Это уравнение в общем виде квадратурой не интегрируется, но может быть заменой переменных сведено к уравнению Бернулли, если известно одно частное решение этого уравнения. Действительно, если x₁ = x₁(t) - известное частное решение, то полагая

получим

Так как

то приходим к уравнению Бернулли