43.Понятие устойчивого положения равновесия автономной системы.

Построим фaзовые траектории на фазовой плоскости системы с постоянными действительными коэффициентами:

(1.9)

Заметим, что начало координат (0,0) всегда является положением равновесия системы (1.9). Это положение равновесия тогда и только тогда является единственным, когда детерминант матрицы отличен от нуля, или что то же, оба собственных значения этой матрицы отличны от нуля.

Рассмотрим скалярные величины x₁, x₂ как координатный столбец векторав двумерном линейном пространстве, в котором фиксирована некоторая ортогональная координатная система; матрицазадает линейный оператортакой, что

(1.10)

Перепишем систему (1.9) в матричной форме:

(1.11)

а также в инвариантной форме:

(2.2)

Определение

Будем говорить, что точка покоя x_i = 0 i = 1…n системы

устойчива, если > 0

> 0 такие, что любая траектория начинающаяся t = t₀ в точке M₀ Uвсе время остается в эпсилон окрестности.

Точка покоя асимптотически устойчива если

1. Она устойчива

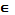
2. > 0 такое что каждая траектория системы начинается в точке M₀ Uстремится к началу координат при t

44.Простейшие типы точек покоя

Решение системы

(2.2)

будем искать в виде x = y =

= 0

л² – (a11+a22)л + a11a22 – a21a12 = 0

(2.3)

1.Корни ХАУРА л₁, л₂ – действительные и различные

X =

Y =

(2.4)

-определяются из (2.3)

с1, с2 – произвольные постоянные

а) Если

l₁ < 0, l₂ < 0.

, то точка покоя M₀ асимптотически устойчива, т.к. из-за наличия множителей

в (2.4) все точки находящиеся в начальный момент при t = t₀ в любой дельта окрестности и начала координат при t стремятся к началу координат

б) l₁ > 0, l₂ > 0.

Этот случай переходит в предыдущий при замене t на –t

в) l₁ < 0 < l₂.

Тогда точка покоя неустойчива, так как движущиеся по траектории x = y =(2.5) точка при сколь угодно малых значениях с1 и при tвыходит из эпсилон окрестности начала координат. В данном случае существует движение приближающееся к началу координат.

x=

При различных значениях с2 получает различные движения по одной и той же прямой y = x

При t точки на этой прямой движутся в направлении начала координат. Точки траектории (2.5) при tдвижутся по прямой y =x удаляясь от начала координат

2.Корни ХАУРА комплексные

л_1,2 = pqi, q0

x=

y=(c1^*+ c2^*sinqt) (2.6)

c1, с2 – произвольные постоянные

c1^*, c2^* - линейные комбинации с1, с2

а) p < 0, q 0

множитель стремится к 0 при t , а второй периодический множитель (2.6) остается ограниченным.

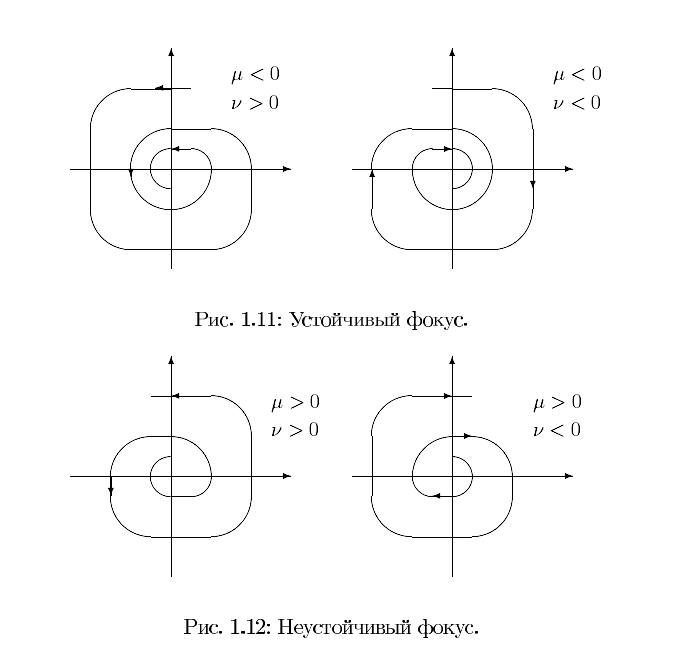
Если p = 0, то траектории в силу периодичности замкнутые кривые, окружающие точку покоя (0, 0)

Наличие множителя превращает замкнутые кривые в спирали, асимптотически приближающиеся при t к началу координат рис (1.11)

б) p > 0, q 0

этот случай переходит в предыдущий при замене t на –t, движение происходит в противоположном направлении рис (1.12)

3. Корни ХАУРА кратные

л1 = л2

а) л1 = л2 < 0

Общее решение имеет вид

X =

Y =

Так как множитель

стремится к 0 при t , точка асимптотически устойчива рис (1.9)

Если == 0 то получаем устойчивый дикритический узел рис (1.8)

Система имеет вид

б) л1 = л2 > 0

заменой t на –t приходим к предыдущему случаю

Замечание

Если detA = 0 (определитель), то у ХАУРА есть л1 = 0

Предположим л1 = 0 л2 0 тогда общее решение

X =

Y =

Исключая t получаем семейство кривых

(y –c1)=(x –c1)

C2 = 0

y =x

Если < 0, то при tна каждой траектории точки приближаются к лежащей на этой траектории точки покоя. Точка покоя устойчива

В этом случае система имеет вид

dy/dx = k

траектории прямые y = kx + c

4. Если л1 = л2 = 0

Положение равновесия вся фазовая плоскость

а) Общее решение

x = c1

y = c2

б) x = c1 + c2t

y = c1^* + c2^*t