Таким образом, получаем дискретный набор стационарных состояний, располагающихся на расходящейся системе энергетических уровней:
В отличие от модели потенциального ящика, энергетические уровни плоского ротатора являются двукратно вырожденными. Вырождение связано с возможностью вращения частицы в двух противоположных направлениях. В модели потенциального ящика коэффициенты суперпозиции для движения частицы направо или налево, жестко заданы: А = –В. В модели же плоского ротатора это коэффициенты могут быть любыми, например A = 1, B = 0 (вращение против часовой стрелки) или A = 0, B = 1 (вращение по часовой стрелке).
Обратимся к рассмотрению волновых функций. Общее решение является суперпозицией двух частных решений:
Ф() = Ае im + Be–im , где m = L/
причем здесь на коэффициенты А и В не накладывается дополнительных условий (кроме условия нормировки), вследствие того, что у цилиндрической ямы нет границ и частица не обязана непрерывно изменять направление движения на противоположное). В результате, для заданных значений наблюдаемых Е и L существует целое двумерное пространство стационарных состояний, одним из базисов которого являются специальные состояния с волновыми функциями:
Ф+() = С+ е im ( A = 1, B = 0 )
Ф– () = С– е–im ( A = 0, B = 1 )
Константы С+ и С– нужны для нормировки волновых функций (в данном случае они одинаковы и равны числу (1/2)1/2. Графики таких функций можно примерно представить в виде спиралей, навивающихся на окружность вращения (для Ф– — по часовой стрелке, для Ф+ — против часовой стрелки). Частота спиралей определяется значением m. Можно заметить, что при m = 0 обе эти комплексные функции вырождаются в действительные константы:
Ф+() = Ф–() = (1/2)1/2.
Физический смысл выбора именно этих двух состояний в качестве базисных заключается в том, что для них является строго определенным направление вращения частицы, а, следовательно, и ориентация вектора L. Все остальные состояния являются суперпозиционными, и для них определенное значение имеют только энергия и длина (модуль) вектора момента |L|, тогда как при измерении проекции вектора Lz мы будем получать случайным образом два возможных результата: +L (с вероятностью А2) и –L (с вероятностью В2).
В полном соответствии с принципом неопределенности, в базисных состояниях указанного вида строго определено направление вращения частицы, и совершенно не определено положение этой частицы на окружности вращения. Если мы рассчитаем вероятность обнаружения частицы в некоторой определенной точке с заданным значением координаты ,
P () = |Ф+()|2 = |Ф–()|2 = (1/2)1/2 = const
то увидим, что эта вероятность не зависит от положения точки. Другими словами, все положения равновероятны, и частица как бы равномерно "размазана" по всей окружности. Существуют, однако, некоторые суперпозиционные состояния, в которых пространственное положение частицы на окружности более определённо. Это такие состояния, для которых коэффициенты суперпозиции имеют следующие значения:
А = В и Ф'() = А (е im + e–im ) ,
A = –B и Ф''() = А (е im – e–im ) .
Применив тригонометрическое представление комплексных экспонент, найдем, что обе эти функции действительные:
Ф'() = 2А cos (m) и Ф'() = 2iА sin (m)
Вследствие взаимной ортогональности, эти две функции образуют еще один базис двумерного подпространства состояний с определенными значениями E и L . Для таких стационарных состояний вероятность найти частицу в некоторой определенной точке окружности уже будет зависеть от положения этой точки:
P' () = (1/2) cos2 (m) P'' () = (1/2) sin2 (m)
Т.о. частица "размазана" по окружности не совсем равномерно, а образует в некоторых областях более плотное облако, а в некоторых — менее плотное. Имеются даже такие точки, где плотность облака равна нулю, т.е. облако разделено узловыми поверхностями на части.
Другими словами, здесь также получается стоячая волна с узлами и пучностями (отрезки синусоид, свернутые в кольцо), но расположенная не вдоль прямой, как для частицы в ящике, а вдоль окружности. Смысл квантования, проявляющегося в данном случае, сводится к тому, чтобы на окружности помещалось целое число полуволн, т.е. чтобы при добавлении еще одного целого поворота максимумы и минимумы волны совпадали с предыдущими (только так можно обеспечить стационарность состояния).
Очевидно, что ориентация вектора L для таких состояний совершенно не определена: при измерении мы будем получать два результата:
Lz = +m и Lz = –m
с одинаковыми вероятностями 1/2.
Подчеркнем то обстоятельство, что при m = 0 эти формулы вырождаются в константы:
Ф'() = (1/2)1/2 и Ф''() = 0.
Можно построить графики и самих волновых функций и их квадратов. Это удобнее сделать в виде т.н. полярных диаграмм, которые строятся следующим образом. Для рассматриваемого значения координаты проведем вектор именно под этим углом из центра окружности, причем длина этого вектора будет равна величине функции при данном значении . Концы всех таких векторов и образуют гладкую кривую — полярную диаграмму функции.
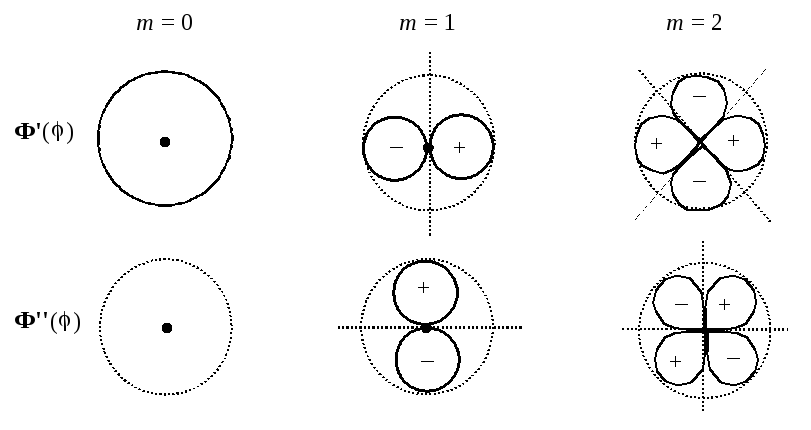
Пунктирными прямыми линиями обозначены узловые плоскости.
Обобщения модели плоского ротатора
Сферический ротатор
В этой модели частица может двигаться не вдоль плоской окружности, а по поверхности сферы. Расстояние от центра (r) по-прежнему является константой. Волновые функции в этом случае становятся двумерными, зависящими от двух переменных, в качестве которых удобно выбрать два угла и (сферическая система координат).
Независимость движений во взаимно перпендикулярных направлениях приводит к тому, что полная волновая функция может быть представлена в виде произведения двух одномерных функций
(, ) = () • ()
Существенное отличие сферического ротатора заключается в необходимости введения уже двух квантовых чисел:
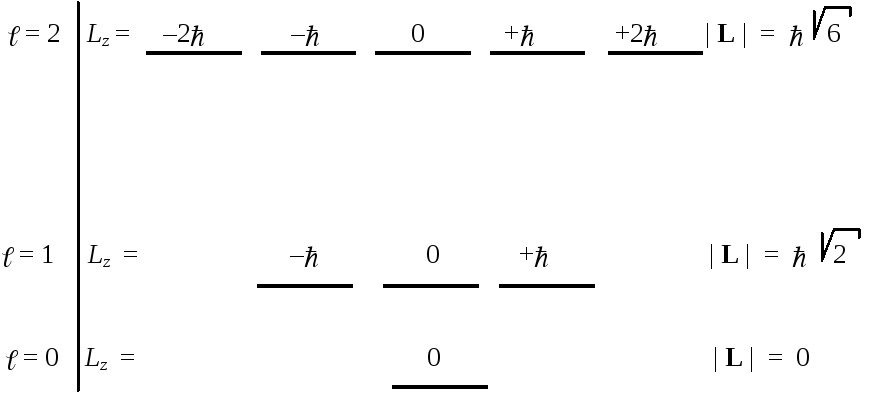
— орбитальное квантовое число ( = 0, 1, 2 . . . .)
m — магнитное квантовое число (m = 0, 1, 2 . . . l)
При заданном значении числа магнитное число m может принимать только значения, не превосходящие по модулю число (всего 2 +1 значение). Допустимые значения наблюдаемых задаются формулами:
| L |2 = 2[( + 1)] , где = 0, 1, 2 , ....
Е = | L |2 / 2I = (2/2I) [( + 1)] = b [( + 1)]
Еще одно отличие заключается в следующем: в случае плоского ротатора направление вектора L всегда совпадало с направлением оси вращения. Другими словами, и сам вектор и его проекция на ось вращения совпадали. В случае сферического ротатора положение оси вращения в системе координат нельзя указать однозначно. Поэтому вектор L уже не обязан совпадать с осью вращения, и проекция этого вектора отличается от самого вектора. Дополнительное квантовое число m как раз и предназначено для определения величины проекции:
Lz = m
Таким образом, сферический ротатор имеет дискретный набор стационарных состояний, расположенных на расходящейся системе энергетических уровней, однако степень вырождения каждого такого уровня иная, чем в случае плоского ротатора.
Каждому уровню энергии соответствует целое подпространство стационарных состояний размерности 2 + 1. У всех этих состояний модуль вектора L строго определен, но ориентация этого вектора является неопределенной. В каждом таком подпространстве можно выделить (2 + 1) базисных состояний, для которых определена также и проекция вектора L на некоторую ось. Остальные состояния — суперпозиционные.
Можно также заметить, что для каждого подпространства можно найти и другой базис, где определена локализация частицы ротатора на поверхности сферы. Явный вид таких функций хорошо известен: это угловые части водородоподобных атомных орбиталей. Так, первому уровню ( = 0) соответствует сферическая орбиталь s-типа. Второму уровню ( = 1) соответствуют три гантелеобразных орбитали р-типа. Третьему уровню ( = 2) соответствуют пять орбиталей d-типа и т.д.
Сферический нежесткий ротатор
В этой модели расстояние от частицы до центра вращения может изменяться, и в результате появляется еще одна степень свободы и еще одно квантовое число n (главное квантовое число). Конечный результат хорошо известен из теории одноэлектронного атома.
Ансамбль ротаторов
В случае, когда ротатор способен взаимодействовать с окружающей средой (термостатом), он уже не остается навсегда в одном из стационарных состояний, а пробегает все доступные ему стационарные состояния с вероятностями, определяемыми значениями энергии (в соответствии с функцией Больцмана).
Существенная особенность ротатора заключается в наличии вырождения энергетических уровней (особенно для сферического и нежесткого ротаторов). Это может привести к тому, что максимальная вероятность может приходиться не на самый низший уровень энергии, а на некоторый возбужденный. Так, например, для вращений молекул при комнатной температуре максимально заселенными являются уровни с вращательными числами = 5 - 8.