40

Матрицы

Матрицы являются математическими объектами, которые, подобно векторам, широко используются для моделирования различных физических и химических структур и их свойств.

Матрица— таблица, состоящая обычно из чисел—матричных элементов. Однако в качестве матричных элементов могут выступать и объекты другого вида — векторы, функции, другие матрицы и т.д. Матрицу удобно представлять в виде упорядоченной совокупностистрокистолбцов. В общем случае, количества строк и столбцов матрицы могут отличаться. Однако, наиболее часто используются квадратные матрицы, в которых число строк равно числу столбцов. Квадратную матрицу принято изображать следующим образом:

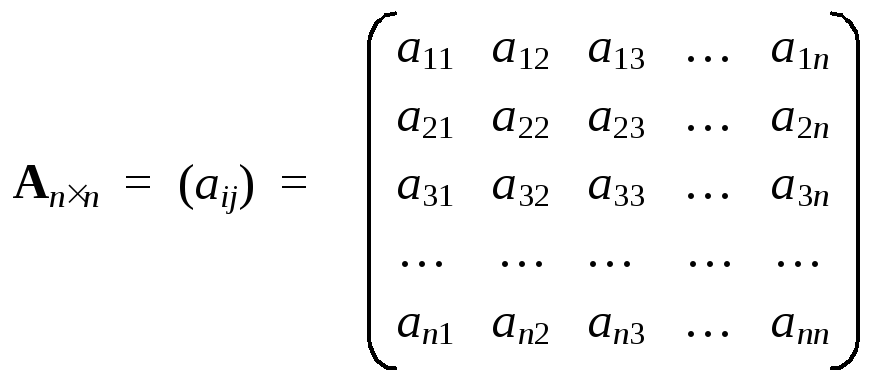
Первый индекс матричного элемента (i) служит номером строки, а второй (j) — номером столбца.

Иногда матрицу удобно рассматривать как вектор-столбец, элементами которого являются вектор-строки, или, наоборот, как вектор-строку, элементами которой являются вектор-столбцы.

Характеристики матриц

Для матриц можно определить несколько полезных характеристик.

Определитель.Подопределителемилидетерминантомматрицы (обозначается какDetили) понимается некоторое число,которое можно рассчитать через матричные элементы по известным правилам.

В основе вычисления определителя лежит процедура разложения по элементам строки. Для ее выполнения необходимо:

1) выбрать в матрице некоторую строку (обычно выбирается та строка, которая содержит наибольшее количество нулей),

2) записать первый элемент выбранной строки и умножить его на вспомогательную матрицу (минор), которая получается из исходной посредством вычеркивания строки и столбца, на пересечении которых стоит выписанный элемент,

3) выполнить описанный выше прием для всех элементов выделенной строки,

4) каждое произведение дополнительно умножить на (–1)^i+j, гдеiиj— индексы элемента выделенной строки,

5) сложить все полученные таким образом произведения элементов выделенной строки на вспомогательные матрицы-миноры.

Полученная сумма и будет представлять собой разложение определителя по элементам данной строки. Это разложение содержит матрицы, размер которых на единицу меньше, чем у исходной матрицы. Теперь необходимо описанную процедуру разложения по элементам строки применить к каждой из этих матриц меньшего размера. В результате получим разложение, содержащее матрицы еще меньшего размера. Продолжая эту процедуру, мы в итоге придем к матрицам размера 11, представляющим собой обычные числа. Теперь необходимо выполнить все арифметические операции умножения и сложения полученных чисел. В результате получим некоторое число, которое и будет определителем исходной матрицы.

Рассмотрим конкретный пример вычисления определителя. Пусть имеется матрица (33):

Выберем для разложения первую строку. Выполним первый этап разложения и получим сумму трех произведений элементов первой строки на вспомогательные матрицы размера (22):

Выполним второй этап, подвергнув процедуре разложения вспомогательные матрицы размера (22) и получим совокупность чисел, связанных определенными операциями умножения и сложения:

2 (55 – 71) – 4(35 – 74) + 8(31 – 54)

Наконец, выполнив все арифметические действия, получим конечный результат:

2 (25–7)–4(15–28) + 8(3–20) =

= 2 (18) – 4(–13) + 8(–17) = 36 + 52 – 136 = – 48

Полученное число и равно определителю матрицы: Det(A) = – 48.

Подчеркнем, что для разложения определителя можно выбирать любую строку и любой столбец на любой из стадий вычисления.

Перманент.Перманент— это число, которое рассчитывается во всем аналогично определителю, за исключением того, что дополнительные множители имеют вид (+1)^i+j= 1. Перманент, поэтому, иногда называют плюс-определителемматрицы. Так, для приведенного выше примера перманент будет равен:

Р (А) = 2(25 + 7) + 4(15 + 28) + 8(3 +20) =

= 2 (32) + 4(43) + 8(23) = 64 + 172 + 184 = 420.

Алгебраическое дополнение.Алгебраическое дополнение— это число, которое можно поставить в соответствие любому матричному элементу. Для вычисления алгебраического дополнения к элементуа_ij необходимо:

1) вычеркнуть в исходной матрице строку с номером iи столбец с номеромj,

2) рассчитать определитель матрицы меньшего размера, которая получится в результате такого вычеркивания,

3) этот определитель необходимо умножить на множитель (–1)^i+j.

Алгебраическое дополнение обозначается той же буквой, что и матричный элемент, но только прописной (А_ij). Очевидно, что определитель матрицы может быть выражен как сумма произведений элементов любой строки (столбца) на их алгебраические дополнения:

Det (A) = a_i1  A_i1 + a_i2  A_i2 + . . . . + a_in  A_in =  (a_ik  A_ik)

След.Следомназывается число, равное сумме всех диагональных (т.е. таких, у которых оба индекса одинаковы) элементов матрицы:

Sр (A) =  a_ii .