Строение В-ва и Осн.Квант.Химии / семинары (текст) / 08-КМ-резонанс

92

СИСТЕМЫ С ЭВОЛЮЦИЕЙ

До сих пор мы рассматривали квантово-механические описания для систем, находящихся в стационарных состояниях. В действительности, микросистемы могут быть приготовлены и в нестационарных состояниях. Такие системы отличаются тем, что они эволюционируют во времени, т.е. числовые значения их наблюдаемых изменяются во времени, причем эта эволюция происходит не хаотически, а по определенному закону.

Ранее (см. тему «Частица в потенциальном ящике») уже было отмечено, что система, приготовленная в начальном состоянии с ненадлежащей энергией (т.е. не соответствующей ни одному из разрешенных стационарных значений), эволюционирует; при этом в ходе эволюции изменяются значения наблюдаемых, в том числе — энергии. Эволюция заканчивается тогда, когда система приобретает одно из разрешенных (стационарных) значений энергии. Несмотря на кратковременность релаксации (для электронных систем  ~ 10^–8 с), такие процессы имеют значение для понимания существа ряда химических задач.

Закон эволюции системы во времени можно описать посредством зависимости вектора состояния (волновой функции) системы от времени. Другими словами, для решения задачи об эволюционирующей системе необходимо найти явный вид зависимостей типа:

|  _t = f (t) или (q)_t = f (q, t)

Общее правило квантовой механики — принцип суперпозиции — заключается в том, что любые, в том числе и нестационарные, состояния могут быть представлены в виде линейной комбинации некоторого набора специальных — базисных — состояний

|  _t = C₁ | 1  + C₂ | 2  + . . . + C_i | i  + … + C_n | n 

где | i  — базисное состояние с номером i. Такое представление позволяет описать вектор состояния максимально детально и связать его с результатами экспериментальных измерений. При необходимости, координатное представление вектора состояния |  _t = (C₁ , C₂, . . . , C_n ) можно изобразить волновой функцией (q, t), где аргумент функции q определяется выбором конкретного базиса.

В квантовой механике обычно используют два варианта подобных ЛК:

1) представление Шредингера

|  _t = C₁^t | 1  + C₂ ^t | 2  + . . . + C_i ^t | i  + … + C_n^t | n 

(от времени зависят только коэффициенты C_i, а сами базисные состояния | i  не эволюционируют);

2) представление Гейзенберга

|  _t = C₁ | 1  ^t + C₂ | 2  ^t + . . . + C_i | i  ^t + … + C_n | n  ^t

(от времени зависят только базисные состояния | i , а коэффициенты C_i имеют постоянные во времени значения)

В представлении Гейзенберга в качестве базисных векторов используются собственные векторы оператора Гамильтона, которые изменяются с течением времени по стандартному закону:

| h_k  = | h_k  • exp(i_kt)

(здесь _k = E_i/ — частота, связанная с энергией i-го стационарного состояния)

Произвольный вектор, эволюционирующий во времени, имеет вид:

|   ^t = С₁ | h₁  + С₂ | h₂  + … =

= С₁ | h₁ • exp(i₁t) + С₂ | h₂  • exp(i₂t) + …

Из этого выражения ясно видна эквивалентность представлений Шредингера и Гейзенберга. В первом случае временные экспоненты следует включить в коэффициенты разложения, а во втором — в базисные векторы.

C_k ^t = C_k  exp(i_kt) | h_k  = | h_k   exp(i_kt)

представление Шредингера представление Гейзенберга

Для получения полной информации об эволюции системы нужно знать:

1) вид пространственных множителей собственных векторов гамильтониана | h_k ;

2) частоты (энергии) стационарных состояний _k ;

3) коэффициенты C₁, C₂, …

Рассмотрим методику применения этой схемы на простом примере эволюционирующей системы — системы с двумерным базисом, которая имеет всего два базисных состояния. Система включает в себя три частицы: два протона, жестко фиксированные на небольшом постоянном расстоянии друг от друга, и один электрон, который может свободно двигаться внутри потенциальной ямы сложной формы, образуемой электрическими полями протонов.

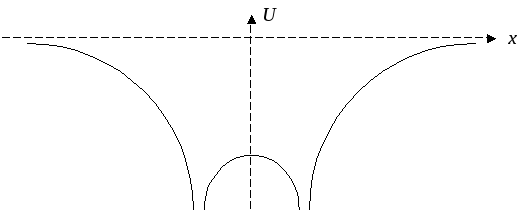
На химическом языке такая система называется молекулярным ионом водорода (Н₂⁺) и представляет собой простейший пример молекулы.

С точки зрения структурной химии всякая молекула состоит из одноядерных фрагментов — химических атомов. Поэтому для электрона, входящего в состав некоторой молекулы, можно определить специальную наблюдаемую, характеризующую "принадлежность" электрона тому или иному атому. В случае молекулярного иона водорода атомов всего два (обозначим их a и b). Следовательно, наша наблюдаемая может иметь только два допустимых значения: X = X_a и X = X_b. Этим значениям соответствуют два допустимых состояния молекулы: | a  и | b.

В квантовой механике измерения любых наблюдаемых определяются некоторой измерительной процедурой, в соответствии с общей схемой:

Такой прибор можно сконструировать и в нашем случае. Это будет микроскопический ящик, разделенный на два одинаковых отсека непроницаемой для электронов перегородкой. В качестве процедуры измерения будем рассматривать процедуру помещения системы в ящик. При выполнении "измерения" каждый из неподвижных протонов попадет в свой отсек, а быстро движущийся электрон должен будет "выбрать" — с каким из протонов он останется.

Этот выбор, очевидно, будет носить случайный характер. Иногда мы будем обнаруживать электрон в первом отсеке, а иногда — во втором. Повторив эту процедуру многократно, мы получим вероятности этих двух возможных исходов процедуры измерения: Р_a и Р_b причем Р_a + P_b = 1. В соответствии с основными постулатами квантовой механики, эти два числа можно рассматривать как квадраты комплексных чисел — амплитуд некоторых событий:

событие 1: "электрон обнаруживается в окрестности протона a" (амплитуда С_a и вероятность Р_a, причем Р_a = |С_a| ²)

событие 2: "электрон обнаруживается в окрестности протона № 2" (амплитуда С_bи вероятность Р_b, причем Р_b = |С_b| ²)

Эту измерительную схему можно изобразить стандартным способом, с использованием понятия спектрального анализатора:

Определенную выше процедуру можно также рассматривать как измерение значения пространственной координаиы х, характеризующей пространственную локализацию электрона, но трактуемую в весьма грубом масштабе (измерительная линейка имеет всего два деления (x_a и x_b). Можно трактовать такие измерения и как определение не самой величины пространственной координаты, а только ее знака: все координаты левой части системы ("в окрестности протона a") отрицательны, а все координаты правой части системы ("в окрестности протона b") положительны.

Всякий спектральный анализатор порождает базисный набор состояний. Это верно и в нашем случае: состояния | a  и | b образуют один из базисных наборов, с помощью которого можно анализировать любые векторы состояний за счет их представления в виде суперпозиции:

|   = C_a | a  + C_b | b 

Такой базис удобно назвать атомным, поскольку каждое из базисных состояний соответствует локализации электрона в окрестности одного из ядер молекулы, или говоря химическим языком, принадлежности электрона одному из химических атомов в составе молекулы.

Воспользуемся атомным базисом для анализа интересующей нас проблемы эволюции системы во времени. Если произвольный вектор |   описывает нестационарное состояние, эволюционирующее во времени, то коэффициенты его разложения по атомному базису будут функциями времени, так как сами базисные состояния атомного базиса от времени не зависят:

|   ^t = C_a ^t | a  + C_b ^t | b 

Следовательно, в атомном базисе мы получаем представление Шредингера.

Явный вид функциональной зависимости коэффициентов разложения от времени задается уравнением Шредингера:

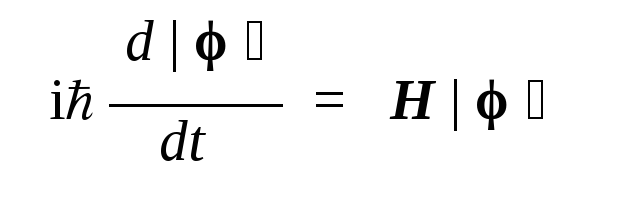
(здесь i — мнимая единица, H — оператор Гамильтона).

Решениями этого уравнения являются векторы|   ^t, выражаемые всевозможными линейными комбинациями собственных векторов оператора Гамильтона: | h₁ , | h₂ , …, | h_n :

|   ^t = D₁ | h₁  + D₂ | h₂  + … + D_n | h_n  =

= D₁ | h₁  exp(i₁t) + D₂ | h₂   exp(i₂t) + … + D_n | h_n   exp(i_nt)

Приведенную выше векторную форму уравнения Шредингера можно перевести в любое координатное представление, в котором вектору состояния будет соответствовать вектор-столбец координат, а оператору — квадратная матрица. Возможна и альтернативная (но полностью эквивалентная) запись в виде системы линейных дифференциальных уравнений:

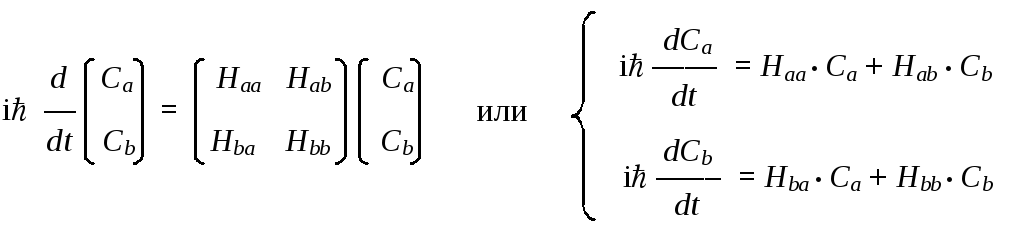
Отсюда видно, что в атомном базисе оператор Гамильтона изображается квадратной матрицей, что позволяет найти явный вид собственных векторов этого оператора | h_i и соответствующих им частот _i, входящих в приведенное выше выражение.

В нашем случае атомный базис является двумерным. Поэтому любой вектор в этом базисе будет иметь всего две координаты, а любой оператор — два собственных вектора. Следовательно, интересующее нас разложение произвольного вектора по собственным векторам гамильтониана приобретет вид:

|   ^t = D₁ | h₁  + D₂ | h₂  = D₁ | h₁  exp(i₁t) + D₂ | h₂   exp(i₂t)

или в координатном представлении:

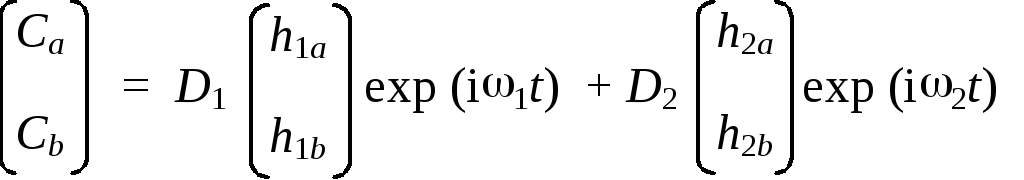
Координаты собственных векторов гамильтониана и соответствующие им частоты можно легко найти, решив уравнение на собственные значения:

Собственные значения гамильтониана Е₁ и Е₂ являются корнями характеристического уравнения ( = 0):

(Н_aa – Е) • (Н_bb – Е) – Н_ab • Н_ba = 0

которые (после некоторых несложных преобразований) в явном виде выражаются формулами:

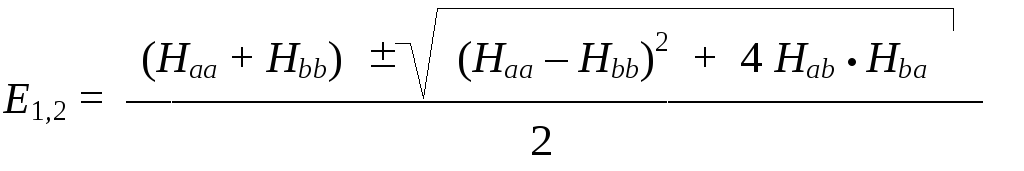
Для конкретного случая рассматриваемой системы это выражение можно существенно упростить, если проанализировать физический смысл матричных элементов гамильтониана. Числа H_ij представляют собой производные по времени от амплитуд переходов между базисными состояниями:

H_aa = d  a | a  / dt H_bb = d  b | b  / dt

H_ab = d  a | b  / dt H_ba = d  b | a  / dt

Вследствие симметрии нашей системы (оба протона совершенно одинаковы) должна наблюдаться симметрия и в матричных элементах оператора: Н_aa = Н_bb и Н_ab = Н_ba. Поэтому обозначим диагональные элементы символом Н (Н_aa = Н_bb = Н), а недиагональные — символом –А (Н_ab = Н_ba = – А). Тогда выражения для энергий существенно упростятся:

Е_1,2 = Н  А.

Найдем теперь координаты собственных векторов. Для этого подставим найденные выражения для энергий в систему и решим ее. При E = Е₁ = Н – А получим h_1a = h_1b ; при E = Е₂ = Н + A получим h_2a = –h_2b .

Теперь можно записать явный вид собственных векторов оператора Гамильтона в выбранном нами базисе:

где ₁ = E₁/ = (Н – А)/ и ₂ = E₂/ = (Н + А)/.

Теперь интересующее нас выражение для координат произвольного эволюционирующего вектора приобретет окончательный вид:

который можно привести к эквивалентной записи в виде системы уравнений:

С_a = D₁  exp (i₁t) + D₂  exp (i₂t)

С_b = D₁  exp (i₁t) – D₂  exp (i₂t)

Эти уравнения задают явный вид зависимости координат вектора состояния от времени. Видно, что характер этой зависимости может быть разным, при разных величинах коэффициентов D₁ и D₂, которые определяются начальными условиями. Другими словами, характер эволюции состояния зависит от того, каково это начальное состояние (в каком месте системы электрон "отпустить на свободу").

Приготовим нашу систему в начальном состоянии |  ^о = | a  , в котором электрон локализован в окрестности левого атома ( a ). В этом случае начальные координаты вектора состояния таковы: С_a^о = 1 и С_b^o = 0.

Подставим эти начальные условия в систему и получим:

1 = D₁ + D₂

0 = D₁ – D₂

поскольку при t = 0 любая экспонента exp (it) = 1.

Отсюда вытекает, что при данных начальных условиях D₁ = D₂ = 1/2 , и, следовательно, эволюция такого начального состояния будет описываться уравнениями:

C_a = [exp (i₁t) + exp (i₂t)] / 2

С_b = [exp (i₁t) – exp (i₂t)] / 2

Квадраты этих коэффициентов (амплитуд) дают нам вероятности обнаружения электрона в окрестности атомов a и b, соответственно. Найдем эти вероятности. Для атома a получим:

Р_a = С_a*  С_a =

= (1/4)[ exp (–i₁t) + exp (–i₂t) ] [ exp (i₁t) + exp (i₂t) ] =

= (1/4)[ exp (–i₁t)  exp (i₁t) + exp (–i₁t)  exp (i₂t) +

+ exp (–i₂t)  exp (i₁t) + exp (i₂t)  exp (i₂t) ] =

= (1/4){ 1 + exp [–i(₁ – ₂)t] + exp [i(₁ – ₂)t] + 1 } =

= (1/4){ 2 + 2 cos [(₁ – ₂)t]} =

(1/2){ 1 + cos [(2A/)t]} = cos²[(A/)t]

(здесь использовано тригонометрическое соотношение 1+ cos = 2 cos²/2)

Выполнив аналогичные вычисления для второго коэффициента, найдем

Р_b = sin²[(A/)t].

Для наглядности можно построить графики этих зависимостей:

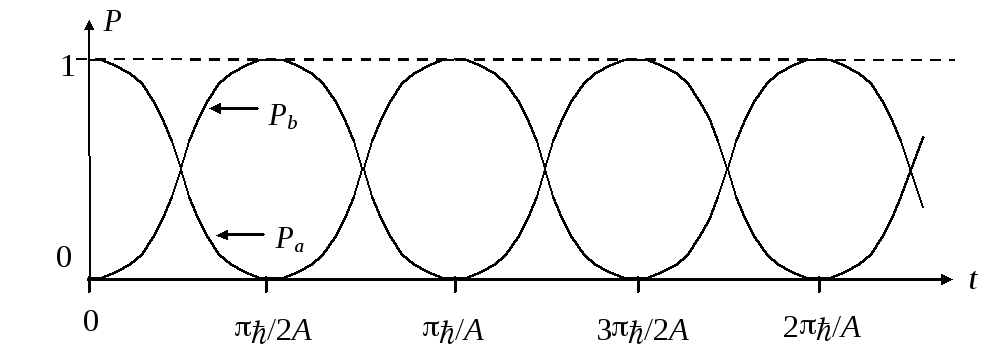
Физический процесс эволюции, описываемый такими зависимостями, выглядит весьма просто. Электронное облако, сосредоточенное в начальный момент времени около левого протона а (Р_a = 1, Р_b = 0), с течением времени постепенно распределяется по всей системе и затем локализуется около правого протона b (Р_a = 0, Р_b = 1), затем процесс идет в обратном направлении, и потом повторяется снова и снова. Другими словами, мы наблюдаем колебательный переход электрона (говоря точнее, электронного облака) от одного протона к другому с постоянной частотой  = (A/), зависящей от величины А (недиагонального элемента оператора Гамильтона). Можно отметить, что эта частота определяется природой ядер атомов и расстоянием между ними.

Если бы наша система была полностью изолирована от окружающей среды, то такие колебания продолжались бы до бесконечности. В действительности, заряженное электронное облако, которое движется колебательным образом, будет излучать электромагнитную волну с частотой  = (A/), уносящую энергию из системы. Это приведет к постепенному (за время ~ 10^–8 c) затуханию колебаний и переходу системы в одно из двух стационарных состояний, описываемых собственными векторами оператора Гамильтона (| h₁  с энергией Е₁ = Н – А или | h₂  с энергией Е₂ = Н + А). Для обоих этих векторов квадраты координат равны между собой, и следовательно, вероятности найти электрон у обоих протонов будут одинаковыми: Р_a = Р_b = 1/2. (Как правило, эволюция заканчивается в стационарном состоянии наименьшей энергией. Оно называется основным состоянием)

Описанный выше колебательный процесс релаксации, сопровождаемый излучением, называется квантовомеханическим резонансом. Ввиду их кратковременности, резонансные процессы релаксации практически никогда не наблюдаются в химических явлениях, однако их нужно всегда иметь в виду в качестве реального механизма достижения стационарных состояний после внешних возмущений химических частиц.

Полученный результат можно обобщить на любые начальные условия. Пусть в начальном состоянии электрон не локализован полностью у одного из протонов, а распределен каким-то произвольным образом, задаваемым коэффициентами С_a^o =  и С_b^o = . Зависимости вероятностей от времени будут определяться выражениями:

Р_a = ² + (² – ²) cos² [(A/)t] и Р_b = ² + (² – ²) sin² [(A/)t]

Графики этих функций имеют точно такой же вид, как и для изученного нами начального состояния, но размах их колебаний меньше — они расположены не в полосе 0 < P < 1, а в полосе ² < P < ².

В предельном случае (² = ² ) ширина полосы становится нулевой и графики вырождаются в прямую линию, параллельную оси времени. Другими словами, такие начальные состояния уже являются стационарными и их эволюция не наблюдается. Таких состояний два, так как приведенное условие (² = ²) выполняется в двух случаях: при  =  . Этот результат мы уже получили ранее, в виде соотношений между координатами собственных векторов оператора Гамильтона.

Стационарные состояния отличаются тем, что плотность электронного облака во всем объеме системы со временем не изменяется и распределение электрического заряда в пространстве является неизменным. Такое неподвижное облако электрического заряда не излучает ЭМ-волны, несмотря на то, что оно образовано движущимся электроном. Именно поэтому стационарные состояния являются единственными долгоживущими состояниями квантово-механических систем (атомов, молекул, ионов).

С химической точки зрения, описанный процесс будет выглядеть так: если сблизить на малое расстояние атом водорода и протон, произойдет КМ-резонанс — система начнет релаксировать колебательным образом. С течением времени придет в устойчивое состояние — образуется молекулярный ион водорода.

Н + Н⁺  (Н₂)⁺ + Е

Можно изобразить процесс резонанса с помощью т.н. корреляционной диаграммы, которая показывает характер изменения энергии в этом процессе.

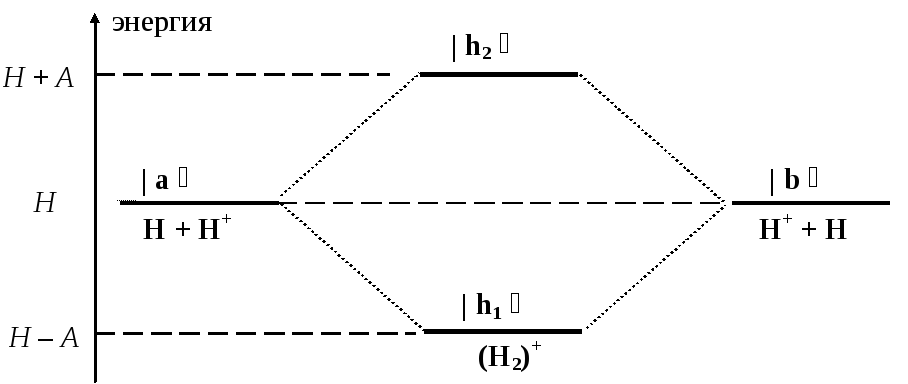
Молекулярный ион в основном состоянии имеет пониженную энергию, по сравнению с состояниями | a  и | b , в которых молекула искусственно разделена на отдельные атомные фрагменты. Избыточная энергия (Е = А) излучается системой в ходе КМ-резонанса в виде электромагнитной волны (за счет пространственных колебаний электрического заряда). Образование любых химических связей при сближении атомов осуществляется посредством КМ-резонанса. Именно в этом смысле надо понимать встречающиеся в литературе утверждения о «резонансной природе» химической связи. Если мы захотим обратить этот процесс и превратить молекулу в два отдельных атома, нам придется вернуть излученную энергию назад, т.е. совершить над молекулой некоторую работу (W = А). Другими словами, на разрушение любой химической связи требуется затрата энергии.

Можно обобщить полученные результаты и на случай несимметричных молекул. Возьмем молекулярный ион гидрида лития (LiH)⁺. Здесь электрон движется в потенциальной яме, создаваемой неподвижным ядерным остовом из протона и иона Li⁺. Анализируя распределение электрона нашим прибором, мы будем находить его (случайным образом) то в окрестности протона, то в окрестности иона Li⁺. Весь рассмотренный выше математический формализм полностью сохранится, за исключением того, что диагональные элементы матрицы оператора Гамильтона теперь уже не будут одинаковыми (Н_aa  Н_bb), так как напряженность электрического поля вблизи малого по размерам протона будет заметно выше, чем возле иона лития. Подчеркнем, что недиагональные элементы останутся равными друг другу по модулю ( | Н_ab | = | Н_ba | = –A ) — это характерная особенность оператора Гамильтона (самосопряженность), справедливая для любых систем.

Поэтому формулы для энергий стационарных состояний и для координат собственных векторов гамильтониана будут иными:

Е₁  Н_aa – А²/(Н_aa – Н_bb) Е₂  Н_bb + А²/(Н_aa – Н_bb)

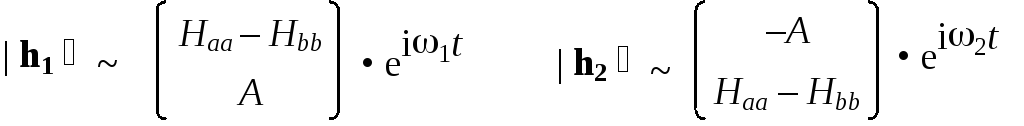
Легко видеть, что теперь координаты собственных векторов не равны друг другу по величине ( | Н_aa – Н_bb | > A ), и, следовательно, пространственное распределение электрона в основном стационарном состоянии уже не будет равномерным: в окрестности протона плотность электронного облака будет выше, чем в окрестности иона лития.

Изменится и вид корреляционной диаграммы — ее качественная структура сохранится, но симметрия будет утрачена:

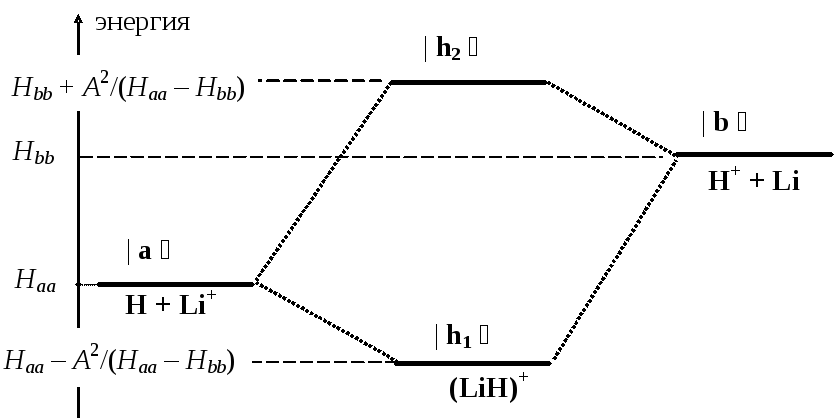
Можно заметить, что при образовании молекулы (LiH)⁺ количество выделяющейся энергии будет разным, в зависимости от начального состояния: реакция H + Li⁺  (LiH)⁺ сопровождается выделением меньшего количества энергии, чем реакция H⁺ + Li  (LiH)⁺. Отсюда следует, что и распад молекулы на атомы будет происходить неодинаково: процесс (LiH)⁺  H + Li⁺ будет происходить легко, с малыми затратами энергии, тогда как процесс (LiH)⁺  H⁺ + Li будет протекать гораздо труднее, поскольку требует больших затрат энергии.

Из сказанного можно вывести еще одно полезное заключение: чем более различны по природе взаимодействующие атомы, тем меньше выигрыш в энергии при обобществлении электронов Е ~ А²/(Н_aa – H_bb) и, следовательно, тем слабее образующаяся химическая связь. Напротив, самые прочные связи характерны для гомоатомных молекул. Например, для связей Н — Х картина выглядит следующим образом:

Атом Х	K	Na	Li	H	Cl	Br	I
Е, кДж/моль	180	197	234	432	427	362	295