28

Глава 1. Атом водорода

Атом водорода является простейшей структурой, представляющей интерес для химии. Задача описания атома водорода играет в квантовой химии фундаментальную роль по ряду причин. Во-первых, волновые функции стационарных состояний атома водорода можно использовать в качестве базисного набора для построения и анализа волновых функций более сложных систем — многоэлектронных атомов и молекул. Во-вторых, атом водорода — это единственная реальная система, для которой возможно установить аналитический вид волновых функций. Эта особенность атома водорода обусловлена тем, что в нем отсутствуют межэлектронные взаимодействия, так как в его составе имеется всего один электрон. (Кроме атома водорода существуют и другие атомные структуры, такие как ионы He⁺,Li²⁺,Be³⁺и т.д., состоящие из единственного электрона и атомного ядра с зарядомq= +Zе. Их описание в качественном отношении полностью совпадает с описанием атома водорода. Поэтому все такие структуры объединяются под названием "водородоподобные атомы". В дальнейшем речь будет идти только об атоме водорода, но полученные результаты будут приложимы ко всем водородоподобным атомам за счет введения в формулы параметраZ— зарядового числа ядра).

Атом водорода состоит всего из двух частиц — электрона и ядра (роль ядра выполняет протон), которые характеризуютсямассами(m₁иm₂),электрическими зарядами(q₁= –еиq₂= +е),спиновыми моментами(s₁= 1/2,s₂= 1/2). Взаимодействия, определяющие характер движения частиц в атоме водорода, весьма разнообразны. За счет наличия противоположных по знаку электрических зарядов, между протоном и электроном действуюткулоновскиесилы притяжения, зависящие от расстояния между электроном и ядром. Кроме того, имеют местомагнитныесилы, обусловленные, с одной стороны, относительным движением заряженных частиц, а, с другой стороны, наличием у электрона и ядра спиновых магнитных моментов. Поскольку для атома водорода кулоновские силы значительно больше (примерно на два порядка) магнитных, в этом случае можно ограничиться построением сравнительно простойнерелятивистской модели, когда всеми разновидностями магнитных взаимодействий полностью пренебрегают.

В такой нерелятивистской модели движение электрона и ядра можно разделить на два независимых типа — внешнееивнутреннее. Внешнее движение сводится к перемещениям обеих частицы как материальных точек в некоторой лабораторной системе координат. Внутреннее движение и электрона, и ядра характеризуется наличием у них собственных механических спиновых моментов (и связанных с ними магнитных моментов). Для начала ограничимся рассмотрением только внешних (пространственных) движений частиц, входящих в состав атома водорода — электрона и протона, без учета их спиновых состояний.

В этом случае вектор состояния атома водорода удобно представить в пространственном базисе:

| =C₁|1+C₂|2+• • •=_C_i|i,

где каждое базисное состояние | iотличается тем, что для него точно известны положения обеих частиц в пространстве относительно фиксированной лабораторной системы координат, т.е. известны 6 чисел-координат (x₁,y₁,z₁,x₂,y₂,z₂)_i. Ясно, что с таким бесконечномерным вектором состояния можно практически работать только после его перевода в функциональное представление —волновую функцию. Эта волновая функция, описывающая любое состояние атома, допустимое законами квантовой механики, должна, в общем случае, зависеть от шести пространственных координат и от времени:Ф=Ф(x₁,y₁,z₁,x₂,y₂,z₂;t). В дальнейшем ограничимся рассмотрением только стационарных состояний, для которых волновую функцию можно представить в стандартном виде:

Ф(x₁, y₁, z₁, x₂, y₂, z₂; t) = Ф(x₁, y₁, z₁, x₂, y₂, z₂)  exp(it), где  = Е/

В результате задача сводится к установлению вида только пространственной части Ф(x₁,y₁,z₁,x₂,y₂,z₂) и энергииЕ, которые можно найти из уравнения на собственные значения для оператора Гамильтона:НФ=ЕФ. Оператор Гамильтона для связанной двухчастичной системы должен включать в себя три слагаемых: два одночастичных оператора кинетической энергии (Т₁иТ₂) и один двухчастичный оператор потенциальной энергии (U₁₂):

Здесь символ ² (иногда вместо него употребляется эквивалентный символ) обозначает одночастичный дифференциальный оператор "набла-квадрат", представляющий собой сумму вторых частных производных по декартовым координатам некоторой частицы:

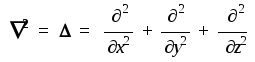
Таким образом, интересующее нас уравнение на собственные значения ("стационарное уравнение Шредингера") имеет вид:

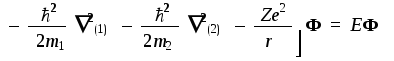
Решениями этого уравнения являются волновые функции, описывающие все возможные стационарные состояния атома водорода, а также соответствующие им энергии (в нерелятивистском приближении, т.е. без учета магнитных эффектов). Если атом изолирован от окружающих тел, то движения частиц в нем можно разделить на два невзаимодействующих типа:

1) глобальноедвижение атома как материальной точки (центра масс) в лабораторной системе координат (X, Y, Z).

2) локальныедвижения частиц во внутренней системе координат (x, y, z), начало которой расположено в центре масс.

Первый тип движения мы можем исследовать "смотря на атом издалека", т.е. полагая его просто материальной точкой без внутренней структуры. Второй тип движения можно исследовать "смотря на атом изнутри" и полагая, что атом как целое является неподвижным. В этом случае наблюдатель находится в центре масс и видит лишь относительное движение электрона и ядра. Независимость внешнего и внутреннего движений позволяет представить шестимерную волновую функцию в виде произведения двух трехмерных функций:

Ф (x₁, y₁, z₁, x₂, y₂, z₂) = Ф' (X, Y, Z)  Ф'' (x, y, z)

Первый сомножитель представляет собой глобальную функцию, описывающую движение атома как целого (т.е. как одной бесструктурной частицы с массой M=m₁+m₂) и удовлетворяет трехмерному уравнению:

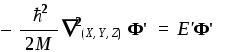
Это стандартное уравнение для свободной частицы с массой М. Его решения известны из модельных квантово-механических задач "свободная частица" и "частица в трехмерном потенциальном ящике" (см. [1]).

Второй сомножитель представляет собой "внутреннюю" функцию, описывающую движение электрона и ядра относительно неподвижного центра масс. Согласованный характер движения электрона и ядра дает возможность заменить их единственной квазичастицей, обладающей массойи движущейся вокруг неподвижного центра масс. Вследствие большого различия в массах электрона и ядра эта квазичастица по своим свойствам практически совпадает с электроном. Поэтому в дальнейшем будем рассматривать ее как обычный электрон с незначительно уменьшенной массой. Внутренняя функция, описывающая движение электрона (квазичастицы), удовлетворяет трехмерному уравнению вида:

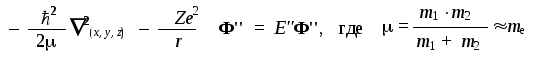
В декартовой системе координат это уравнение невозможно сделать более простым, так как входящая в него переменная rзависит от всех трех декартовых координат электрона:r²=x²+y²+z². Поэтому целесообразно перейти ксферической системе координат, в которой переменнаяrявляется одной из трех независимых координат. Замена производится по правилам:

x=r sincos;y=rsinsin;z=r cos

где угол отсчитывается в вертикальной плоскости от осиZи изменяется в интервале от 0 до, а уголотсчитывается в горизонтальной плоскости от осиXи изменяется в интервале от 0 до 2. После замены переменных волновая функция изменит свой вид:Ф''(x,y,z)(r,,), а стационарное уравнение Шредингера приобретет такую форму:

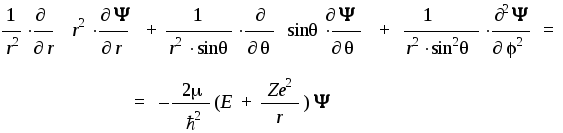
Сделанная замена переменных позволяет представить трехмерную функцию в виде произведения трех одномерных функций-сомножителей:

(r,,) =R(r)()()

которые являются решениями системы из трех одномерных уравнений:

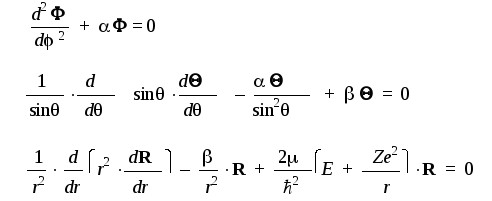
Необходимо отметить, что в результате разделения в уравнениях появились две новые константы —  и, которые учитывают существующие взаимосвязи между уравнениями и их решениями. Эти параметры должны иметь одни и те же значения во всех уравнениях, куда они входят. Данное условие выполняется только для некоторых "разрешенных" значений, образующихдискретный набор, а именно: = 0, 1, 4, 9, 16, 25, … и= 0, 2, 6, 12, 20, 30, 42, …

С целью упрощения этих рядов удобно ввести два новых вспомогательных параметра — иm, для которых выполняются более простые условия:

 = ( + 1) , где= 0, 1, 2, . . .

 =mm, гдеm= 0,1,2, . . .

Дискретность в решениях R-,- и-уравнений, вызываемая приведенными ограничениями для параметров и, приводит, в свою очередь, к дискретности допустимых значений энергии атома, связанной с его внутренним движением:

Целые числа, входящие в приведенные формулы, называются квантовыми числами атома водорода:n—главное,—орбитальное,m—магнитное. Они выступают в роли параметров, нумерующих возможные решения уравнения Шредингера, или, что то же самое, волновые функции стационарных состояний:

(r,,) =R(r)•()•() = (n,,m) =R(n,) •(,m) •(m) =

= R(n,) •Y(,m)

Произведения (,m) •(m)= Y(,m) называютсяшаровыми функциями.

Приведем явный вид R- , - и -функций (в сферических координатах).

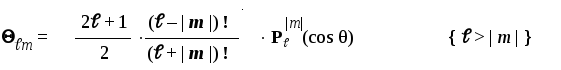
В этом уравнении символом Р(cos) обозначен т.н. "присоединенный полином Лежандра" (степении порядка |m|) — некоторая степенная функция от (cos). Явный вид этих полиномов можно найти в математических справочниках или вычислить по следующей формуле:

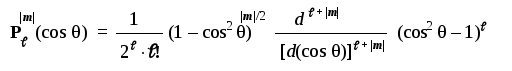
Для R-уравнения решения имеют вид:

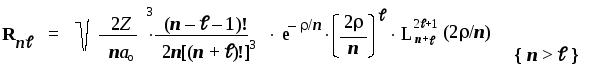
Здесь символом L обозначен т.н. "присоединенный полином Лаггера" (степени (n+) и порядка (2+ 1) — степенная функция от переменной, которая представляет собой новую шкалу расстояний:= (Z/a_o)r, прокалиброванную с помощью т.н. "атомных единиц длины" а_о= 4_o²/e²0,053 нм (здесь константа_o= 8,8410^–12ф/м — т.н. "диэлектрическая постоянная").

Явный вид присоединенных полиномов Лаггера можно найти по формуле:

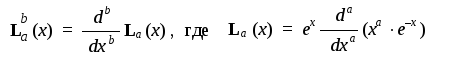
Стоящие впереди полиномов Лежандра и Лаггера сложные выражения являются нормировочными множителями, которые при задании конкретных величин квантовых чисел приобретают простой вид.

Следует обратить внимание на важное обстоятельство. В формулы входят некоторые величины, являющиеся факториалами. Эта функция определена только для целых неотрицательных чисел. В результате, на допустимые совместные (т.е. относящиеся к одному состоянию атома) значения квантовых чисел накладываются ограничения, указанные выше в фигурных скобках.

_{Для иллюстрации можно привести некоторые конкретные выражения для волновых функций с небольшими номерами.}

R_n,-функции(нормировочные множители опущены):

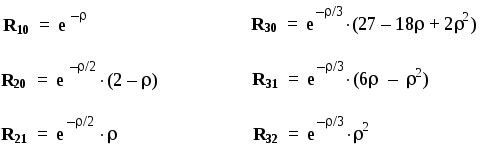
(В обозначениях функций первый числовой индекс равен главному квантовому числу n, а второй — орбитальному квантовому числу.)

- функции (нормировочные множители опущены):

Ф-функции (нормировочные множители опущены):

Располагая таблицами таких функций, можно легко построить явный вид волновой функции для любого стационарного состояния атома водорода. Пусть состояние характеризуется квантовыми числами {n,,m} = {2, 1, –1}. Тогда волновая функция будет иметь вид (нормировочный множитель опущен):

Полный вид волновой функции получим при умножении этой пространственной части на временной экспоненциальный множитель:

 _{(2, 1, –1), t}=_{(2, 1, –1)}  exp[i(E₂/)t] ,

где Е₂— энергия, соответствующая значениюn= 2.

Обозначаемые тремя индексами функции _n,,mчасто называют водородными атомными орбиталямиили Н-АО. Заметим, что в большинстве случаев они содержат комплексную экспоненту и, следовательно, являются комплекснозначными функциями. Это обстоятельство часто отмечается и в названии —комплексные атомные орбитали(КАО).

Существует еще одна, более удобная номенклатура Н-АО. Каждый тип АО обозначается определенным символом — латинской буквой, — указывающим на значение орбитального квантового числа:

Значение 	0	1	2	3	4	5	…
Символ	s	p	d	f	g	h	…

Впереди буквы-символа указывается значение главного квантового числа, а магнитное квантовое число обозначается цифровым подстрочным индексом, следующим за буквой-символом. Например:

 ₁₀₀ = 1s_o

 ₂₀₀ = 2s_o  ₂₁₀ = 2p_o  _21–1 = 2p_–1  ₂₁₁ = 2p₁

 ₃₀₀ = 3s_o  ₃₁₀ = 3p_o  _31–1 = 3p_–1  ₃₁₁ = 3p₁

 ₃₂₀ = 3d_o  ₃₂₁ = 3d₁  _32–1 = 3d_–1. . . и т.д.

В ряде случаев бывает более удобным использование не самих волновых функций, а некоторых линейных комбинаций, построенных из этих функций, с целью получить чисто действительные функции. Такие линейные комбинации строятся в виде суммы или разности двух КАО, у которых все квантовые числа одинаковы по величине, но магнитные числа противоположны по знаку. У таких пар КАО R- и-сомножители в точности одинаковы, поскольку они не зависят от знака магнитного числа. В результате получаем суммы и разности комплексно сопряженных экспонент, которые сводятся к действительным тригонометрическим функциям (здесь нормировочные множители опущены):

_{(n, , m)} +_{(n, , –m)} =R( e ^im e ^{–im}) = R • cos (m=⁺_{( n, , |m|)}

_{(n, , m)} –_{(n, , –m)} =R( e ^im –e ^{–im}) = R • sin (m= ^–_{( n, , |m|)}

Такие линейные комбинации называются действительными атомными орбиталями(ДАО). В их обозначениях нижний индекс заменяется на буквенный. Например:

(2р₁+ 2р_–1) ~ 2p_x (2р₁– 2р_–1) ~ 2p_y 2р₀~2p_z

(3d₁+ 3d_–1) ~ 3d_xz (3d₁– 3d_–1) ~ 3d_yz

(3d₂+ 3d_–2) ~ 3d_(x²_{– y}²₎ (3d₂– 3d_–2) ~ 3d_xy 3d₀~ 3d_z²

ДАО удобны в том отношении, что их можно изображать графически, анализировать различные пространственные характеристики и симметрию. Подчеркнем, что наборы КАО и ДАО полностью эквивалентны в математическом отношении и представляют собой два базисных набора в одном и том же пространстве состояний (см. модель "плоский ротатор" в [1]).

Кроме чистыхсостояний, описываемых волновыми функциями типа_n,,m, существует множество состоянийсмешанных(илисуперпозиционных):

_n,=С₁(2р_–1) +С₂(2р₀) +С₃(2р₊₁)

_n=С₁(2s) +С₂(2р₊₁)

 = С₁(1s) +С₂(2р₊₁)

Все такие функции, составленные из слагаемых с разными значениями квантовых чисел nи/или, описываютнестационарныесостояния, которые в течение короткого времени редуцируют к одному из стационарных состояний типа_{n ,m}, в которых все три квантовые числа точно определены. Исключением из этого общего правила являются суперпозиционные функции типа_n,. Редукция таких состояний может быть вызвана только действием внешних причин (например, магнитного поля).