Термическая релаксация

Вероятности, вычисляемые по формуле Больцмана, характеризуют равновесное состояние системы в контакте с термостатом. Можно, однако, искусственно приготовить систему, находящуюся в неравновесном состоянии, где заселенности уровней энергии не соответствуют больцмановским вероятностям. В процессе энергообмена с термостатом такая система будет релаксировать к состоянию равновесия, т.е. значение ее энергии будет медленно (по сравнению с флуктуациями) дрейфовать к равновесному значению: EE.

Неравновесная в термическом отношении ситуация возникает всякий раз, когда в термический контакт с термостатом, имеющим температуру , приводится система, приготовленная при другой температуре*. Если выполняется условие* <, то наблюдается направленный поток термической энергии из термостата в систему. При этом температура внутри системы повышается и, в конце концов, становится равной температуре термостата:*. Если выполняется условие* >, то наблюдается направленный поток термической энергии из системы в термостат. При этом температура внутри системы понижается и, в конце концов, становится равной температуре термостата:*.

При термическом равновесии выполняется условие _сист=_терм. Соответственно, при равновесии порции термической энергии одинаково часто переносятся как из термостата в систему, так и из системы в термостат, а средняя энергия системы и ее температура остаются постоянными. Другими словами, любая система, приведенная в термический контакт с термостатом, вынуждена "подстраиваться" под его температуру.

Подчеркнем, что свойства самого термостата при таких процессах термической релаксации не изменяются. Это обусловлено тем обстоятельством, что термостат всегда гораздо больше погруженной в него системы.

Большой канонический ансамбль (бка)

Эта модель предназначена для описания открытых систем, которые способны обмениваться с окружающей средой как термической энергией, так веществом (частицами):Econst,Nconst.

Для таких систем окружающая среда выполняет две роли. Во-первых, она выступает в качестве термостата — резервуара термической энергии. Во-вторых, она является резервуаром вещества(частиц). Процесс обмена частицами между системой и резервуаром называетсядиффузионным контактом. Если система содержит частицы разных сортов, то в окружающей среде можно выделить несколько резервуаров вещества — по одному для каждого сорта частиц. Например, для системы, в которой протекает реакция синтеза аммиака, получим следующую модельную схему, включающую один термический и три диффузионных контакта:

При анализе состояния открытой системы необходимо принимать во внимание конкретные значения ряда переменных:

E_i— термическая энергия, захваченная системой из термостата,

N₁,N₂, … ,N_n— числа частиц каждого сорта, захваченных системой из резервуаров вещества.

Рассмотрим для примера систему, представляющую собой ящик с электронами, помещенный в магнитное поле. Число электронов может меняться, так как они могут проникать внутрь системы из резервуара и уходить в него обратно. При этом каждый электрон может поглощать из термостата порцию энергии E= 2H, ориентируясь своим вектором магнитного момента "против поля", или отдавать эту порцию обратно в термостат, ориентируясь вектором магнитного момента "по полю". Соответственно, получаем набор возможных состояний системы:

Из рисунка видно, что БКА (Econst,Nconst) можно рассматривать как совокупность КА, каждый из которых характеризуется вполне определенным и постоянным числом частиц (Econst,N=const), так же как любой КА можно рассматривать как совокупность МКА, каждый из которых характеризуется постоянной энергией (E =const,N=const).

Каждое из различающихся между собой состояний должно характеризоваться определенной вероятностью. В модели БКА эти вероятности зависит от термической энергии и чисел частиц: P=f(E,N₁,N₂, … ,N_n).

Если у системы имеются состояния, вырожденные как по энергии, так и по числам частиц все сортов, то они будут равновероятными.

Явный вид выражения для вероятности задается формулой:

P = (1/Z)  exp[–(E – ₁N₁ – ₂N₂ – … – _nN_n)/]

Экспонента в этом выражении выполняет роль, аналогичную фактору Больцмана в модели КА и называется фактором Гиббса. Нормировочный множительZназываетсябольшой статистической суммой.

Величины Еихарактеризуют термический контакт системы с термостатом:Е— захваченная из термостата термическая энергия,— температура термостата.

Величины _iиN_iхарактеризуют диффузионный контакт системы с резервуаром частицi-го сорта.N_i— число захваченных из этого резервуара частиц, а_i — характеристика резервуара, аналогичная температуре термостата. Она называетсяхимическим потенциаломрезервуара. Так же, как и статистическая температура, химический потенциал имеет размерность удельной энергии (в расчете на одну частицу). Если температура отражает плотность термической энергии в термостате, то химический потенциал отражает плотность вещества (частиц) в резервуаре.

В ряде случаев вместо химического потенциала бывает удобнее использовать т.н. активность, определяемую с помощью равенств:

 = exp(/) или=ln

Для иллюстрации методики применения модели БКА рассмотрим простой пример, связанный с адсорбцией молекул газа на поверхности твердых тел. Выделим в качестве системы микроскопический участок поверхности, размером в одну молекулу — т.н. адсорбционный центр. Эта система может находиться всего в двух состояниях: свободном и занятом:

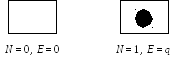
(здесь q— теплота адсорбции)

Большая статистическая сумма в данном случае будет состоять всего из двух слагаемых:

Z = exp [– (E₁ – N₁)/] + exp [– (E₂ – N₂)/] =

= exp [– (0 – 0)/] + exp [– (q – )/] = 1 +   exp (– q/)

Соответственно, вероятности обнаружения системы в свободном и занятом состояниях будет равны:

P₁= 1/ZиP₂=exp(–q/)/Z

В теории адсорбции обычно пользуются специальной величиной — степенью заполнения(), которая представляет собой долю поверхности адсорбента, занятую адсорбированными молекулами и которая, очевидно, просто равна вероятностиР₂.

Это уравнение можно переписать в другом виде, с использованием таких величин как давление газа ри адсорбционный коэффициентb.

В таком виде данное уравнение хорошо известно как адсорбционная изотерма Лэнгмюра. Первоначально оно было найдено экспериментальным путем, но видно, что его можно получить как элементарное следствие из модели БКА. Более того, в этом случае можно сразу установить важную взаимосвязь между адсорбционным коэффициентом, температурой и теплотой адсорбции.

Таким образом, открытая система находится в термическом контакте с термостатом и в диффузионном контакте с резервуаром. При равновесии обмен энергией и частицами происходит с одинаковой частотой в обоих направлениях. Поэтому средняя величина энергии и среднее число частиц внутри системы остаются неизменными, за исключением флуктуаций. Относительная величина этих флуктуаций зависит от размеров системы. Если система макроскопическая (порядка 1 моля), то флуктуациями как энергии, так и числа частиц можно пренебречь.

Тем не менее, можно искусственно приготовить систему с "неправильным" числом частиц N*N. Такая система будет, очевидно, неравновесной и мы будем наблюдать направленный поток вещества: еслиN* <N, этот поток будет направлен внутрь системы, если жеN* >N, то наружу. В конечном итоге система подстроится под свойства резервуара, с которвм она находится в диффузионном конктакте.

Формальным условием диффузионного равновесия является равенство внешнего и внутреннего химических потенциалов:

_{системы}=_{резеврвуара}

аналогично тому, как условием термического равновесия является равенство внутренней и внешней температур:

_{системы}=_{термостата}