Микроканонический ансамбль (мка)

Эта модель применима для систем, в которых две величины являются строго постоянными:

1) полная энергия E= const,

2) число частиц N=const.

Такие системы обычно называются изолированными, так как они лишены возможности обмениваться с окружающей средой и энергией, и веществом (частицами). Тем не менее, обмен другими наблюдаемыми (импульсом, моментом импульса, спином) возможен. В таких системах также не должны протекать химические реакции, приводящие к изменению числа частиц. Функция распределения МКА выглядит максимально просто — все вероятности одинаковы:

Р₁=Р₂=Р₃= … =P_n= 1/

где — полное число доступных системе состояний.

Следовательно, среднее по ансамблю имеет вид:

A_a=P₁A₁+P₂A₂+ … +P_nA_n= (1/)A_i

В качестве примера рассмотрим частицу в трехмерном ящике с шероховатыми стенками. Такая частица отражается от стенок ящика хаотическим и непредсказуемым образом. Полная энергия ее сохраняется, но импульс может изменяться (по направлению). Пусть нас интересует положение частицы, т.е. ее пространственные координаты x,y,z. Ясно, что ни одна из точек внутри ящика не лучше всех остальных и, следовательно, вероятность обнаружить частицу в любой точке одна и та же:

P(x,y,z) =const

Вычислим среднее значение координаты х.

х_a=х_i/

Поскольку в данном случае спектр наблюдаемой непрерывный, нужно от суммы перейти к интегралу:

Неопределенный коэффициент вычислим из условия нормировки (полная вероятность найти хотя бы какое-нибудь допустимое значениехдолжна равняться 1, т.е.p_i= 1):

Тогдах_a =L_x /2 . Аналогично найдем: y_a =L_y /2 иz_a =L_z /2 .

В качестве второго примера возьмем электрон в изолированном ящике и рассмотрим наблюдаемую, которая называется "проекция вектора спина на ось z". Для электрона она может иметь только два допустимых значения: (S_z )₁= +/2 и (S_z )₂= –/2. Этим значениям спектра соответствуют равные вероятностиР₁=Р₂= 1/2. Следовательно, среднее значение наблюдаемойS_zбудет равно:S_z = (+/2 )  (1/2) + (–/2 )  (1/2) = 0.

Теперь увеличим размер системы — вместо одного поместим в наш изолированный ящик сразу 10 электронов. У такой многочастичной системы имеется важная особенность. Для нее можно определить две разновидности наблюдаемой S_z:

1) локальныепроекцииS_z, характеризующие конкретные электроны,

2) глобальнуюпроекциюS_z, характеризующую всю систему целиком.

Ясно, что значение глобальной наблюдаемой будет просто складываться из значений локальных:

S_z = (S_z)₁+ (S_z)₂+ … + (S_z)₁₀

Хотя по физическому смыслу локальные и глобальная наблюдаемые не отличаются, они относятся к разным объектам и имеют различные спектры. Для каждой локальной наблюдаемой спектр состоит всего из двух допустимых значений: S_z =/2 с одинаковыми вероятностямир= 1/2. Для глобальной наблюдаемой спектр включает в себя 11 допустимых значений (в единицах):

S_z = { +5, +4, +3, +2, +1, 0, –1, –2, –3, –4, –5 }

Для вычислении среднего значения глобальной наблюдаемой S_zпонадобятся одиннадцать вероятностей — по одной для каждого допустимого значения этой величины. Будут ли они равны друг другу так же, как в случае локальных наблюдаемых? Ответ на этот вопрос отрицательный. Причина неравенства вероятностей заключается в том, что одно и то же значение глобальной наблюдаемой может реализоваться несколькими способами. Предположим, чтоS_z = +4. Отсюда следует, что 9 из 10 локальных векторов спина направлены вверх, а один — вниз. Ясно, однако, что вниз может быть направлен любой из 10 векторов. Следовательно, глобальное состояние может реализоваться десятью способами, разными с точки зрения локального состояния (глядя изнутри), но неразличимыми с точки зрения глобального состояния (глядя снаружи).

Число способов реализации некоторого глобального состояния можно легко подсчитать по известной комбинаторной формуле сочетаний:

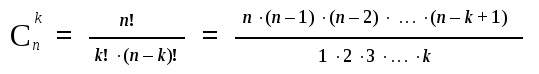
Результат подсчета выглядит следующим образом:

Sz/	+5	+4	+3	+2	+1	0	–1	–2	–3	–4	–5
	1	10	45	120	210	256	210	120	45	10	1

Из таблицы видно, что общее число локальных состояний нашей 10‑электронной системы =_i= 1024, но большинство из них являются неразличимыми при взгляде снаружи. Все 1024 локальных состояния группируются всего в 11 глобальных состояний, различимых снаружи по значению глобальной наблюдаемойS_z.

По определению, для МКА все состояния равновероятны, но это правило относится только к локальным состояниям. Вероятности глобальных состояний будут, естественно, пропорциональны числам способов их реализации через локальные состояния:

P_i=_i/=_i/ 1024

Соответственно, формула для расчета среднего значения глобальной наблюдаемой S_z будет выглядеть так:

S_z /= (+5)(1/1024) + (+4)(10/1024) + … + (–5)(1/1024) = 0

Числа _i, характеризующие различимые глобальные состояния статистических систем, играют важную роль в статистической механике. В большинстве реальных случаев эти числа очень велики и для удобства практического использования их переводят в логарифмическую форму:

_iln_i=_i

Число _i, характеризующее некоторое глобальное состояние статистической системы, называетсястатистической энтропиейэтого состояния. Для макроскопических систем (например, 1 моль газа) даже статистическая энтропия оказывается чрезмерно большой. В этом случае более удобным вариантом является т.н.термодинамическая энтропия:

S_i=k  ln_i=k  _i

где коэффициент перевода k= 1,3810^–23Дж/мольК называетсяпостоянной Больцмана.

Неразличимость локальных состояний в пределах одного глобального состояния приводит к тому, что многочастичные статистические системы, описываемые моделью МКА, выглядят в определенной степени упорядоченными— различные глобальные состояния реализуются с различными вероятностями. Другими словами такая система проводит в одних глобальных состояниях больше времени, чем в других. Для иллюстрации этой неоднородности полезно использовать графические изображения глобальной функции распределения. Для одноэлектронной системы такая функция изображается горизонтальной прямой линией, а для 10-электронной системы — характерной колоколообразной кривой.

По мере увеличения числа частиц в системе выпуклость кривой становится все более резкой. Например, для 100 электронов ее вид будет следующим:

Это означает, что обнаружить подобную систему со значением глобальной наблюдаемой S_z, сколько-нибудь заметно отличающимся от 0, чрезвычайно маловероятно.

Если перейти к макроскопическим системам, в которых число частиц порядка числа Авогадро (~10²³), то подобные кривые полностью вырождаются в вертикальную прямую, расположенную в точке среднего значения наблюдаемой. В этих случаях флуктуации статистических систем практически исчезают, их величина становится настолько малой, что обнаружить их обычными средствами не представляется возможным.

Можно сказать, что в такой ситуации (N) статистический характер системы исчезает, несмотря на то, что она находится в контакте с окружающей средой. Соответственно, изменяется и смысл макронаблюдаемой — она фактически перестает быть усредненной величиной, так как в любой конечной последовательности измерений мы будет получать всегда один и тот же результат: {S_z,S_z,S_z,S_z, …. }.

В этом случае мы снова возвращаемся к схеме классической механики, где значение наблюдаемой выражается не функцией распределения, а одним-единственным определенным числом. Такой предельный случай статистической механики называется равновесной термодинамикой.

Многочастичные системы имеют еще одну важную особенность. Если проследить за одночастичной системой в процессе ее флуктуаций, то мы обнаружим полную хаотичность переходов этой системы между доступными ей состояниями. В многочастичных системах это не так. Вернемся снова к нашей 10-электронной системе. Приготовим ее в таком начальном состоянии, что S_z = +4 и позволим ей флуктуировать под влиянием окружающей среды. Различные переходы между локальными состояниями будут осуществляться полностью хаотически, т.е. будут равновероятными. Однако при взгляде снаружи, когда мы обнаруживаем только переходы между глобальными состояниями, картина получается иной.

Налево, к глобальному состоянию с S_z = +5система может перейти в результате 10 случайных переходов, а число переходов, ведущих систему направо, к состоянию с S_z = +3, равно 450. Естественно, что наблюдая за системой, приготовленной в начальном состоянии сS_z = 4, мы обнаружим у неевыделенное направление эволюции— система, как правило, будет эволюционировать направо — в направлении увеличения— и только в очень редких случаях в противоположную сторону — в направлении уменьшения.

На основании этого вывода можно сформулировать полезное правило: направление эволюции неравновесной системы во времени определяется возрастанием числа  или энтропии. Направленность эволюции будет исчезать при достижении системой среднего значенияS_z , которое соответствует максимально возможной энтропии системы. Абсолютного выражения данная тенденция достигает в случае термодинамических систем (N), для которых тенденция уже становится однозначным законом природы, не допускающим исключений. Этот закон называетсявторым началом термодинамики. Его можно сформулировать так:

а) все самопроизвольные процессы в изолированных системах сопровождаются возрастанием энтропии; процессы с уменьшением энтропии могут протекать только вынужденно, за счет совершения внешней работы, т.е. требуют нарушения условия изолированности системы.

б) все самопроизвольные процессы в изолированных системах заканчиваются при достижении термодинамически равновесного состояния с максимальной энтропией.

Подчеркнем, что в малых статистических системах этот закон имеет только характер тенденции, с его нарушениями мы будем встречаться тем чаще, чем меньше количество частиц имеющихся в системе.