5. Частицы со спином

Для иллюстрации методики применения математического аппарата рассмотрим наблюдаемую, называемую спиновым моментом (или просто спином) микрочастиц. Спин является характеристикой векторного типа, для задания которой необходимо указать:

• длину (модуль) вектора спина | S |,

• направление (ориентацию) вектора спина в пространстве, которую можно определить, например, указанием проекций этого вектора на декартовы координатные оси S_x, S_y и S_z .

Когда мы говорим, что спин — наблюдаемая величина, то подразумеваем, что должна существовать экспериментальная процедура, позволяющая установить как длину, так и направление вектора S. Эта процедура основана на известном физическом законе: если частица обладает электрическим зарядом и участвует во вращательном движении, то масса частицы приводит к появлению у нее механического момента (S), а заряд — к появлению магнитного момента (). Другими словами, у любой заряженной и вращающейся частицы имеются сразу два момента — механический и магнитный, связанные между собой соотношением:

где коэффициент  называется магнитно-механическим отношением. Его величина и знак зависят от заряда и массы частицы. Например:

Наличие магнитного момента у частиц со спином и позволяет построить надлежащий спектральный анализатор. Если частицу с магнитным моментом  поместить в магнитное поле с индукцией В, то ее энергия изменится на величину, зависящую от взаимной ориентации этих двух векторов:

E = –  • B = – |  |  | B |  cos  = – _B  B

Если магнитное поле будет неоднородным, т.е. | В | = f(x, y, z), то величина магнитной энергии будет зависеть и от положения частицы в пространстве, т.е. от величины магнитной индукции в данной точке пространства. В результате, на частицу будет действовать механическая сила, толкающая частицу в область более сильного поля (при параллельной направленности векторов  и В) или в область более слабого поля (при антипараллельной направленности векторов  и В):

Величина этой механической силы зависит от угла  между векторами  и B, что приводит к пространственному разделению частиц со спином, имеющих разную ориентацию вектора спина (и вектора магнитного момента) по отношению к направлению внешнего магнитного поля.

Реальное физическое устройство, которое осуществляет такое пространственное разделение и сортировку частиц со спином, называется прибором Штерна-Герлаха (ШГ). Этот прибор состоит из двух длинных постоянных магнитов особой формы, создающих в промежутке между ними неоднородное магнитное поле с вертикально направленным градиентом. Через промежуток, "заполненный" неоднородным магнитным полем, пропускается пучок частиц со спином, приготовленных в некотором состоянии. Когда частицы пролетают внутри прибора, они отклоняются от первоначального направления, причем величина отклонения зависит от ориентации вектора спина относительно самого прибора.

Конфигурация силовых линий магнитного поля в поперечном сечении такого прибора имеет вид, изображенный на рис. , что обеспечивает повышенную напряженность возле острия нижнего магнита.

Эта конфигурация поля приведет к тому, что частицы с магнитным моментом, ориентированным вверх, будут отклоняться тоже вверх (в область слабого поля), и наоборот. В результате, узкий начальный пучок частиц растянется на выходе из прибора вдоль вертикальной оси z. Величина отклонения частицы за время ее пролетания через прибор будет определяться величиной проекции ее вектора  на вертикальную ось ( _z ):

где L — длина прибора, а v — скорость движения частиц.

Расставив на выходе прибора детекторы, мы сможем легко определять для каждой частицы величину вертикального отклонения, а из него — рассчитывать ориентацию векторов  и S (точнее — проекции этих векторов на вертикальную ось _z и S_z). Кроме того, измеряя максимальные отклонения вверх и вниз, мы можем оценить и длину этих векторов, поскольку максимально возможная проекция всегда совпадает с самим вектором.

Таким образом, прибор ШГ является спектральным анализатором, предназначенным для измерения двух наблюдаемых:

• S_z, называемой проекцией вектора спина (на ось z);

• | S |, называемой модулем вектора спина.

Эти два числа полностью характеризуют сложную наблюдаемую, называемую спином частицы.

Обратимся теперь к анализу результатов измерений, получаемых с помощью прибора ШГ.

Основываясь на классических представлениях о векторных величинах, можно было бы предположить, что ориентации вектора спина могут быть любыми — от параллельной, до антипараллельной. В этом случае, на выходе из прибора мы наблюдали бы некоторую сплошную зону, внутри которой плотность пучка могла бы заметно меняться, но не обращаться в ноль. Для каждого значения наблюдаемой S_z можно измерить вероятность и описать ее функцией распределения, которая могла бы иметь такой примерный вид:

Опыт, однако, показывает иную картину. Действительные функции распределения, получаемые в приборе ШГ, состоят из небольшого числа острых дискретных максимумов, разделенных пустыми промежутками:

Это говорит о том, что наблюдаемая S_z имеет дискретный спектр, состоящий из небольшого числа допустимых значений. Число максимумов n (т.н. мультиплетность) и их положения в функции распределения строго постоянны для каждого типа частиц и никогда не изменяются. В зависимости от способа приготовления частиц (т.е. от их начального состояния) могут изменяться лишь относительные величины пиков.

Отсюда следует важный физический результат:

• длина (модуль) вектора спина строго определена природой частицы и всегда имеет только одно значение (| S | = const),

• ориентация вектора спина может осуществляться только несколькими различными способами (S_z = S_z1, S_z2, . . . , S_zn ), число которых (n — мультиплетность) зависит только от природы частицы и величины модуля спина,

• вероятности различных ориентаций (P₁, P₂, . . ., P_n) вектора спина зависят от конкретных условий приготовления частицы со спином.

На основании этих результатов вводятся некоторые вспомогательные величины (с целью удобства описания спиновых свойств частиц):

• спиновое квантовое число s, величина которого удовлетворяет соотношению n = 2s + 1;

• магнитное спиновое квантовое число m_s, причем m_s = –s, –s + 1, –s + 2, . . . . , s – 2, s – 1, s

Через эти новые вспомогательные характеристики удобно выражать допустимые значения наблюдаемых, характеризующих спин:

Так, для электронов, независимо от способа их приготовления мультиплетность всегда равна 2, откуда следуют соотношения:

Для частиц другой природы — ядер дейтерия — мультиплетность всегда равна 3, откуда следуют аналогичные соотношения:

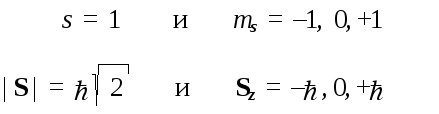
Легко заметить, что целочисленные значения мультиплетности приводят к тому, что спиновые квантовые числа бывают только двух сортов: а) целые (при четной мультиплетности) и б) полуцелые (при нечетной мультиплетности). Это обстоятельство позволяет разделить все микроскопические объекты на два класса:

• бозоны — частицы с целым спином (s = 0, 1, 2, . . .);

• фермионы — частицы с полуцелым спином (s = 1/2, 3/2, . . .).

Такое разделение очень важно, так как бозоны и фермионы принципиально отличаются друг от друга по многим параметрам и той роли, которую они играют в образовании структур. Так, многие важные в химическом отношении свойства атомов и молекул обусловлены именно тем обстоятельством, что электроны относятся к классу частиц-фермионов. Многие свойства света обусловлены тем, что фотоны относятся к классу частиц-бозонов.

Обратимся теперь к рассмотрению формального квантово-механического описания некоторых экспериментов с прибором ШГ.

Пусть имеется пучок частиц со спином 1 (например, ядер дейтерия). Пропустим такой пучок, содержащий N частиц через прибор ШГ. На выходе мы обнаружим три вторичных пучка, содержащие соответственно N₊, N₀ и N_– частиц:

Повторяя много раз этот эксперимент, мы увидим, что числа N₊, N₀ и N_– каждый раз будут несколько отличающимися, однако, их средние значения будут стремиться к некоторым постоянным пределам — вероятностям:

(N₊ / N )  Р₊ (N_o / N )  Р_o (N_– / N )  Р_–

Как всякий спектральный анализатор, прибор ШГ задает набор базисных состояний. В данном случае таких состояний будет всего три:

| +Z  — частица характеризуется величинами m_s = +1 и S_z = +,

| оZ  — частица характеризуется величинами m_s = 0 и S_z = 0,

| –Z  — частица характеризуется величинами m_s = –1 и S_z = –,

Произвольное начальное состояние может быть представлено в виде ЛК этих трех состояний:

|   = Z₊ | +Z  + Z_о| оZ  + Z_–| –Z  ,

где | Z₊ | ² = P₊ ; | Z_o | ² = P_o ; | Z_– | ² = P_– .

Таким образом, в данном базисе вектор состояния может быть изображен набором трех чисел: |   = (Z₊, Z_о, Z_–), где числа-координаты представляют собой амплитуды попадания частицы, находящейся в начальном состоянии |  , в один из базисных пучков:

Z₊ =  +Z |   Z_о =  oZ |   Z_– =  –Z |  

Физическая интерпретация полученного результата такова.

Произвольное состояние |   является суперпозицией трех базисных состояний. В результате применения прибора происходит превращение ("редукция") этого суперпозиционного состояния в одно из базисных состояний.

Другими словами, пока частица находится в исходном пучке, мы не знаем, какой результат даст нам измерение. Мы даже не можем отличить частицы исходного пучка друг от друга. Все что можно сказать о свойствах конкретной частицы сводится к указанию трех вероятностей (Р₁, Р₂, Р₃) или амплитуд (Z₊, Z_o, Z_–). Однако после прибора каждая частица приобретает вполне определенное значение наблюдаемой и ее состояние становится одним из базисных.

Модифицируем экспериментальную ситуацию: на пути всех вторичных пучков поставим еще по прибору ШГ, точно такому же, как и первый:

Результат будет выглядеть так:

• все частицы верхнего пучка после второго прибора ШГ окажутся снова в верхнем пучке;

• все частицы среднего пучка после второго прибора ШГ окажутся снова в среднем пучке;

• все частицы нижнего пучка после второго прибора ШГ окажутся снова в нижнем пучке.

Другими словами, если частица находится в одном из базисных состояний прибора, то повторное применение того же самого прибора не изменяет этого состояния.

На математическом языке этот результат можно сформулировать так: амплитуды перехода между различными базисными состояниями одного и того же прибора равны 0, а между одинаковыми состояниями — равны 1.

оZ | +Z = –Z |+Z = +Z | oZ = –Z | oZ = +Z | –Z = oZ | –Z = 0

 +Z | +Z  =  oZ | oZ  =  –Z | –Z  = 1

Для выражения этого результата удобно использовать матрицу амплитуд переходов:

или т.н. "символ Кронекера":  j | i  = _ij , равный 1 для одинаковых индексов (_ij = 1 при i = j) и 0 для разных индексов (_ij = 0 при i  j).

В математике два вектора, скалярное произведение которых равно 0, называются ортогональными. Поэтому можно сформулировать правило:

все базисные состояния, задаваемые некоторым прибором, попарно ортогональны между собой.