Переход к другому базису

Возьмем прибор ШГ и "положим его на бок", т.е. ориентируем градиент поля вдоль оси y, а не осиz, как это было ранее. Пропустим через прибор пучок частиц, в точности такой же, как и в предыдущих случаях. Очевидно, что этот пучок расщепится прибором на три вторичных пучка. Отличие будет заключаться в том, что отклонение пролетающих частиц будет происходить не в вертикальной плоскости (вдоль осиz), а в горизонтальной плоскости (вдоль осиy):

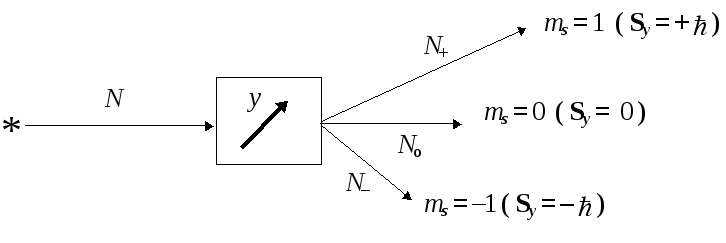
Исследовав результаты анализа, мы сможем представить вектор в виде ЛК трех базисных состояний:

| =Y₊ |+Y+Y_о|оY+Y_–|–Y,

где | Y₊ |²=P₊ ; |Y_o |²=P_o ; |Y_– |²=P_– .

Таким образом, в данном базисе вектор состояния может быть изображен набором трех чисел | = (Y₊,Y_о,Y_–), где числа-координаты представляют собой амплитуды попадания частицы, находящейся в начальном состоянии |, в один из базисных пучков:

Y ₊=+Y|Y _о=oY|Y _–=–Y|

Заметим, что базисные состояния теперь другие, они отличаются от прежних. В новых базисных состояниях определенное значение имеет проекция вектора спина не на ось z, а на осьy. Соответственно, тот же самый вектор задается другими числами-координатами. Другие значения будут иметь и вероятностиP_i.

|   = Z₊ | +Z  + Z_о| оZ  + Z_–| –Z  = ( Z₊ Z_о Z_– )

|   = Y₊ | +Y  + Y_о| оY  + Y_–| –Y  = ( Y₊ Y_о Y_– )

Таким образом, мы получили два различных координатных представления одного и того же вектора состояния. Достаточно очевидно, что аналогичных представлений мы можем получить сколько угодно — для этого достаточно, например, ориентировать прибор ШГ в каком-то промежуточном направлении между осями yиz.

Любые два представления будут взаимосвязаны между собой некоторым унитарным оператором U, который выглядит так:

Например,

Обратное преобразование:

Легко видеть, что матрицы этих двух преобразований эрмитово сопряжены по отношению друг к другу. В то же время они и взаимно обратны, т.е выполняется условие унитарности:

U^–1 = U⁺

Матричные элементы этих матриц оператора можно найти, анализируя вторичные пучки прибора ШГ с z-ориентацией прибором ШГ сy‑ориентацией (или наоборот).

ПОСЛЕДОВАТЕЛЬНЫЕ ИЗМЕРЕНИЯ

На примере спина удобно рассмотреть важную проблему квантовой механики — проблему последовательных измерений.

Рассмотрим классический аналог частицы со спином. В качестве такого аналога выступает массивный шар, вращающийся вокруг оси и, вследствие этого, приобретающий механический момент(момент импульса)L.

Вектор Lможно описать с помощью трех его проекций на декартовы оси:

L = L_x • i + L_y • j + L_z • k = (L_x , L_y , L_z ),

причем между длиной вектора и его координатами существует связь:

| L|²= (L_x)² + (L_y)² + (L_z)²

Другими словами, для классического вектора момента мы можем измерить все три его проекции и длину независимыми способами. При этом, все четыре величины выражаются числами и не зависят от порядка проведения измерений.

Теперь вернемся к неклассическому моменту — спину. Для получения описания спина классическим способом нам необходимо экспериментальное измерение трех величин — либо всех трех проекций (S_x,S_y,S_z), либо любых двух проекций и модуля |S|.

Нам уже известно, что один прибор ШГ позволяет измерить модуль вектора спина и одну из его проекций. Поэтому, очевидно, что для полного описания вектора спина необходимо выполнить не менее двух измерений посредством двух приборов ШГ, ориентированных разными способами (например, по осям zиy). Отметим характерную особенность измерений над микрообъектами: невозможно поместить частицу сразу в два прибора и одновременно выполнить два измерения. Любые два измерения требуют двух разных приборов и поэтому такие измерения должны выполняться последовательно, одно за другим.

Пропустим пучок частиц через прибор ШГ Z-типа. В результате получим три вторичных пучка. Исследуя интенсивности этих пучков, мы найдем точное значение модуля спина |S| (из максимального отклонения) и три амплитуды (вероятности), описывающие наблюдаемуюS_z. Другими словами, наблюдаемая будет описываться:

волновой функцией(z) = ( Z₊,Z_o,Z_–),

функцией распределения P(z) = (P₊= |Z₊ |²,P_o= |Z_o |²,P_–= |Z_– |²)

Пропустим точно такой же пучок частиц через прибор ШГ Y-типа. В результате снова получим три вторичных пучка. Исследуя интенсивности этих пучков, мы найдем то же самое значение модуля спина |S| и три амплитуды (вероятности), описывающие наблюдаемуюS_y. Эта наблюдаемая будет описываться:

волновой функцией(y) = ( Y₊,Y_o,Y_–),

функцией распределенияP(y) = (P₊= |Y₊ |²,P_o= |Y_o |²,P_–= |Y_– |²)

Наконец, использовав прибор ШГ Х-типа, получим аналогичный результат: такое же значение модуля спина и проекцию спина S_xв виде:

волновой функции (х) = ( Х₊,X_o,X_–),

функции распределенияР(х) = (P₊= |X₊ |²,P_o= |X_o |²,P_–= |X_– |²)

Многократно повторяя эти процедуры, мы обнаружим, что получаемые результаты полностью воспроизводятся. Это дает нам возможность приписать частицам:

одно, строго определенное значение длины вектора спина | S|,

три функции { (х),(y),(z) } или { Р(х), Р(y), Р(z) }, описывающие проекции вектора спинаS_x ,S_y ,S_z .

Таким образом, важное отличие квантово-механических описаний от классических заключается в представлении некоторых наблюдаемых функциями распределения (векторами, волновыми функциями), а не числами.

Три полученных нами волновые функции для проекций вектора спина взаимосвязаны. Характер этой взаимосвязи, однако, иной, чем в классическом варианте.

В классическом варианте ситуация такова: если увеличить длину одной из проекций, то другие проекции, соответственно, будут меньше. Другими словами, классическая взаимосвязь относится к длинам проекций вектора.

В квантовом варианте ситуация выглядит иначе: взаимосвязь относится к т.н. "ширине" функции распределения ().

Если ширину одной из функций уменьшить, то ширины других функций распределения станут больше. Смысл этого утверждения можно проиллюстрировать следующим образом.

Попробуем уменьшить ширину одной из функций распределения. Для этого изготовим источник, приготавливающий частицы в одном из собственных состояний прибора ШГ z-типа, например | оZ . Тогда измерение наблюдаемойS_zдаст следующий результат: все частицы, выпущенные источником, попадут в средний базисный пучок прибора:

В этом случае мы можем утверждать, что наблюдаемая S_zимеет строго определенную величину (S_z= 0), а функция распределения(z) имеет ширину, равную нулю (_z= 0).

Теперь измерим другую проекцию, например S_y. В процессе измерения частицы исходного пучка распределятся по трем базисным пучкам прибора ШГy-типа, причем ни одна из вероятностей (амплитуд) не будет равна 0.

В этом случае мы уже не можем утверждать, что наблюдаемая S_yимеет какое-либо определенное значение — в результате измерения может быть обнаружено любое из допустимых значений (+, 0 и –) с вероятностями Р₊, Р_ои Р_– , соответственно.

Теперь поступим обратным способом: попробуем сделать более узкой функцию распределения для наблюдаемой S_y. Для этого приготовим частицы в начальном состоянии, совпадающим с одним из базисных состояний прибора ШГy-типа, например |оY.

Результаты измерения наблюдаемых S_zиS_yбудут выглядеть так:

при измерении S_zполучим некоторую функцию распределения:

при измерении S_yполучим только одно значение с вероятностью 1:

На графиках функций распределения полученные результаты будут выглядеть примерно так:

Можно сделать такое обобщение: ширины функций распределения некоторых наблюдаемых взаимосвязаны, так что искусственное сужение одной из них ведет к уширению другой (и наоборот).

В тех случаях, когда наблюдаемые имеют сплошной спектр, их функции распределения непрерывны. Рассмотренная нами взаимосвязь может быть выражена количественно в таком виде:

_x•_y/2 ;_x•_z/2;_z•_y/2

Эти формулы часто называют "соотношениями неопределенностей" Гейзенберга.

С физической точки зрения, полученный нами результат можно сформулировать так:

• существуют взаимосвязанные пары наблюдаемых, которым невозможно одновременно приписать точные численные значения,

• уменьшение неопределенности (ширины функции распределения) в одной из таких наблюдаемых вызывает увеличение неопределенности (ширины функции распределения) в значении другой.

Эта физическая формулировка часто называется "принципом неопределенности" Гейзенберга.

Теперь можно поставить вопрос так: какие именно пары наблюдаемых связаны между собой "принципом неопределенности", а какие — нет?

Точный ответ на этот вопрос можно сформулировать, воспользовавшись понятием оператора наблюдаемой. Для любой пары таких операторов ( АиВ) можно построить комбинацию, называемуюкоммутатором:

С_АВ=А•В–В•А= [AB]

Если коммутатор равен нулю, то операторы называются "коммутирующими" друг с другом, если коммутатор не равен нулю, то операторы называются "не коммутирующими".

Соответственно, две наблюдаемые АиВвзаимосвязаны (в смысле "принципа неопределенности"), если их операторы не коммутируют, и не взаимосвязаны, если их операторы коммутируют.

_A=f(_B) еслиС_АВ0

_Af(_B) еслиС_АВ= 0

Это заключение легко объясняется следующим математическим правилом: коммутирующие операторы имеют совпадающие собственные векторы, а не коммутирующие операторы не имеют совпадающих собственных векторов.

Следовательно, два спектральных анализатора, измеряющие коммутирующие наблюдаемые, имеют одинаковые базисные состояния. Это может приводить к таким результатам:

В этом случае выделенный одним из приборов базисный пучок больше уже не расщепляется. Поэтому мы можем приписать частицам одновременно две точно определенных наблюдаемых: A = A_i и B = B_j.

Такие наблюдаемые называются совместно-измеримыми.

Два спектральных анализатора, измеряющие некоммутирующие наблюдаемые, не имеют общих базисных состояний. Результаты последовательных измерений выглядят так:

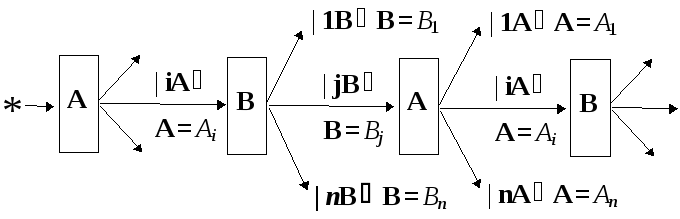
В этом случае каждая наблюдаемая до измерения другой наблюдаемой имеет строго определенное значение, но утрачивает его после измерения. Можно сказать и так, что измерение одной из наблюдаемых, делает значение другой наблюдаемой неопределенным. Поэтому невозможно приписать обеим наблюдаемым точные значения — одна из них обязательно должна выражаться функцией распределения. Такие пары наблюдаемых называются совместно-неизмеримыми.

Таким образом, в квантовой механике все наблюдаемые можно разбить на пары:

совместно-измеримые, для которых функции распределения не связаны между собой соотношениями неопределенности и для которых операторы коммутируют,

совместно-неизмеримые, для которых функции распределения связаны между собой соотношениями неопределенности и для которых операторы не коммутируют,

Примером совместно измеримых наблюдаемых являются, например, энергия и модуль спина, модуль спина и одна из его проекций:

[ E , |S| ] = 0 [ |S| ,S_x] = [ |S| ,S_y] = [ |S| ,S_z] = 0

Примером совместно-неизмеримых наблюдаемых являются две различные проекции спина, импульс и координата, энергия и время.

[ | S | , S_x ]  0 [ | S | , S_y ]  0 [ | S | , S_z ]  0

[ x , p_x ]  0 [ y , p_y ]  0 [ z , p_z ]  0 [ E , t ]  0

Наличие совместно-неизмеримых пар наблюдаемых приводит иногда к важным последствиям в отношении поведения микроскопических объектов. Проанализируем два важных случая.

Механический момент

В классической механике вектор момента всегда связан с вращением объекта вокруг некоторой пространственной оси. Направления как этой оси, так и вектора момента строго определено.

В квантово-механическом случае ситуация иная: нам может быть точно известна только длина вектора и одна из его проекций. Поэтому такому вектору невозможно приписать определенное направление. Вектор может быть направлен множеством способов, и его возможные положения образуют конус, ось которого совпадает с осью прибора, использованного нами для измерения:

Таким образом, некоторые из классических механических характеристик приобретают определенную специфику на микроуровне.

Импульс и положение

В классической механике предполагается, что в каждый момент времени частица имеет и строго определенное положениев пространстве, и строго определенныйимпульс(скорость движения). В квантовой механике операторы координаты и импульса не коммутируют между собой, и поэтому хотя бы одна из этих физические характеристики должна быть описаны функцией распределения.

Для примера рассмотрим модель одномерного потенциального ящика, в котором заперта микроскопическая частица. Частица может двигаться вдоль одного направления х.

Измеряя пространственную координату частицы, мы будем получать различные значения, заключенные в интервале от x= 0 доx=L, и выразить их вероятности в виде некоторой функции распределенияF(x). Аналогичную функцию распределения мы получим и для импульса частицыF(p_x). Обе эти функции характеризуются некоторыми ширинами_х и _p, связанными соотношением неопределенности

_x•_p/2 илиx•p_x/2

Мы можем уменьшить или увеличить ширину функции F(x), изменяя размер ящика (т.е. передвигая одну из стенок). Такое вмешательство приведет к соответствующему изменению ширины функцииF(p_x). Можно заметить, что с импульсом частицы однозначно связана такая важная механическая характеристика, как кинетическая энергия:T = p²/2m. Неопределенность в значении импульсаp_x приведет к существованию неопределенности в кинетической энергииТ.

Ее величину можно выразить так: Т=TT= (рр)²/2m=

= р²/2m2р•р/2m+ (р)²/2m=T+ 0 +T, т. е.

Из последнего выражения мы можем сделать важный вывод: по мере уменьшения размеров ящика (системы), внутри которого заключена частица, кинетическая энергия этой частицы будет возрастать по квадратичному закону. Наоборот, при увеличении размеров ящика кинетическая энергия частицы будет уменьшаться.

Так, электроны, вынужденные двигаться внутри маленького атома, имеют большую кинетическую энергию. При объединении двух атомов в молекулу, объем доступного пространства для каждого электрона увеличивается, а их кинетическая энергия, соответственно, уменьшается.

Такое уменьшение энергии электронов является одной из причин образования химических связей между атомами. Можно сказать, что существование химических явлений (а, следовательно, и химиков) целиком обязано факту несоизмеримости пространственных координат и соответствующих импульсов.

120