Квантовомеханические операторы

В формализме квантовой механики, наряду с вектором (функцией) состояния, важную роль играет понятие оператора.

В математическом смысле оператор представляет собой некоторую процедуру(операцию), выполняемую над векторами. Например, "оператор поворота"R() поворачивает любой вектор на заданный угол, "оператор проектирования"Р(х) переводит вектор в его проекцию на осьхи т.д.

Если начальный и конечный векторы выразить через их координаты в виде векторов-строк или векторов-столбцов, то оператор можно изобразить в виде квадратной матрицы:

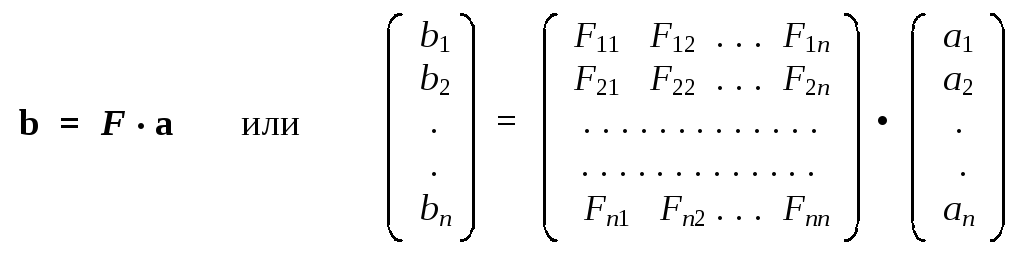
В тех случаях, когда оператор относится к наблюдаемой с дискретным спектром, его всегда можно изобразить посредством матрицы (совокупности чисел — матричных элементов). Если же наблюдаемая имеет непрерывный спектр, то сопоставляемая оператору матрица должна была бы иметь бесконечно большой размер, так что использовать ее для практических вычислений было бы невозможно. В такой ситуации вместо векторов состояния следует использовать их функциональные представления (волновые функции). Соответственно, вместо матричной формы операторов следует использовать алгебраические или аналитические процедуры (преобразования). Их наглядными примерами могут служить:

оператор дифференцирования,переводящий некоторую функцию (первообразную) в ее производную

оператор интегрирования,переводящий некоторую функцию (производную) в ее первообразную

Представления операторов

Явный вид оператора, так же как и явный (координатный) вид вектора состояния, зависит от выбранного базиса. Другими словами, наряду с представлениями вектора состояния, мы имеем и соответствующие представления операторов. Такие представления взаимосвязаны между собой и могут быть преобразованы друг в друга посредством унитарных операторов. Рассмотрим операторное уравнение вида: b = F • a. В двух разных базисах, переход между которыми осуществляется двумя взаимно обратными унитарными операторамиU₂₁иU₁₂, это уравнение будет выглядеть по-разному:

Связь между представлениями оператора Fбудет выглядеть так:

( F)₁=U₁₂ •(F)₂•U₂₁и (F )₂=U₂₁ •(F)₁•U₁₂

Спектральные свойства операторов

Каждый оператор Fимеет некоторый набор собственных векторов (f₁,f₂, ... ,f_n) и собственных чисел или собственных значений (f₁,f₂, ... ,f_n), которые удовлетворяют т.н. "уравнению на собственные значения":

F • f = f • f

Этот набор:

называется спектром оператора.

Типы операторов в квантовой механике

В абстрактной математике операторы могут быть бесконечно разнообразными. Однако в формализме квантовой механике используются лишь три типа операторов.

Операторы квантовомеханических наблюдаемых

Выберем некоторую наблюдаемую Аи возьмем набор базисных состояний соответствующего спектрального анализатора (т.е. таких состояний, в которых наблюдаемаяАимеет строго определенные численные значения:А=А_i). Теперь построим операторА, для которого векторы указанных базисных состояний будут собственными векторами, а указанные значения наблюдаемой — собственными значениями. Такой оператор, являющийся, в сущности, математической моделью спектрального анализатора (и процедуры измерения), и будет называться оператором квантово-механической наблюдаемой А.

Таким образом, каждой наблюдаемой можно сопоставить математический объект — оператор наблюдаемой.Эти операторы обладают рядом полезных свойств и позволяют в компактной и удобной форме записывать многие квантово-механические уравнения.

Наиболее часто понятие оператора используется для следующих целей. Предположим, что явный вид оператора Анекоторой наблюдаемойАнам известен. Тогда, решив "задачу на собственные значения", мы найдем, с одной стороны,

• набор допустимых значений наблюдаемой А (т.е. ее спектрА₁,А₂,... ),

• набор собственных векторов (или функций), описывающих такие состояния, в которых наблюдаемаяАимеет строго определенное значение (одно из допустимых).

Собственные векторы любого оператора обладают одним полезным свойством — они всегда образуют один из возможных базисных наборов, который можно использовать для разложения (анализа) произвольных векторов и функций состояния.

Типичный пример представляет собой т.н. "стационарное уравнение Шредингера"

H=E

Решив это уравнение, мы найдем набор волновых функций, собственных для оператора Гамильтона (Н), каждая из которых описывает особое состояние системы с точно известной и постоянной энергией:

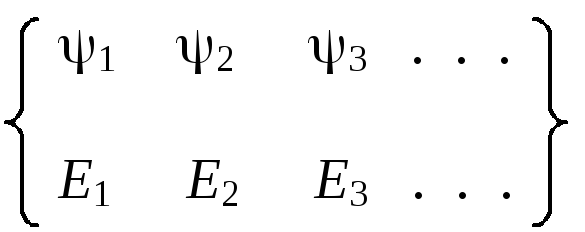
Любая волновая функция может быть представлена в виде ЛК этих собственных функций оператора Гамильтона:

 = С₁ ₁+С₂ ₂+С₃ ₃+ . . .

Пусть система находится в определенном состоянии, которое описывается вектором состояния | или волновой функцией(х). Построим следующую конструкцию:

 A  =   | A |   = _ ^*A  dx

Если вектор | _k(или функция) является собственным для оператораА, то выполняется соотношение A|_k=A_k |_k. Следовательно,

 A  =  _k | A | _k  =  _k | A_k | _k  = A_k  _k | _k  = A_k

(Вектор | _kпредполагается нормированным, поэтому его скалярный квадрат_k|_k= 1.)

Если вектор | (или функция) не является собственным для оператораА, то его можно предварительно разложить в суперпозицию собственных векторов:

| =С₁|₁+С₂|₂ + …

Тогда

A| =С₁ A|₁ +С₂ A|₂ + … = С₁ A₁ |₁ +С₂ A₂|₂ + …

Соответственно:

 A =|A|=

= (₁|С₁* +₂|С₂* + …)•(С₁ A₁ |₁ +С₂ A₂|₂ + …)

Раскрыв скобки, получим сумму произведений типа:

C_j*C_i A_i  _j | _i 

В тех случаях, когда индексы iиj различны, такие произведения будут равны нулю, поскольку разные собственные векторы оператораАортогональны:_j|_i= 0 приij. В итоге в сумме останутся только произведения вида:

C_i*C_i A_i  _i | _i  = C_i*C_i A_i

где P_i= C_i*C_i представляют собой вероятности обнаружения определенных численных значений наблюдаемойА=А_i. Тогда получим:

 A =|A|=Р₁А₁+Р₂А₂+ …

Комбинация, стоящая справа, представляет собой т.н. "математическое ожидание" или среднее значение случайной величины. Таким образом, рассматриваемая здесь конструкцияA =|A|при вычислении дает среднее значение для любой наблюдаемойА, выражаемой функцией распределения.