Базисные состояния и координаты

Координатное представление любого вектора (R) сводится к его изображению посредством линейной комбинации(ЛК) базисных векторов (e₁, e₂, ... , e_n):

R =R₁ e₁+R₂ e₂+ ... +R_n e_n .

Для этой конструкции употребляются также названия "суперпозиция базисных векторов" и "разложение по базису".

Координаты вектора (R₁, R₂, ... ,R_n) в заданном базисе показывают количественный вклад каждого базисного вектора в суммарный вектор. Поскольку при этом свойства базисных векторов предполагаются точно известными, знание координат позволяет предсказывать свойства вектораRбез проведения какого-либо специального исследования этих свойств.

При координатном представлении вектора состояния используется точно такой же прием:

• любой кет-вектор может быть представлен в виде ЛК базисныхкет-векторов

| S  = | 1   S₁ + | 2   S₂ + . . . = |iS_i

• любой бра-вектор может быть представлен в виде ЛК базисныхбра-векторов

 D| =D₁1| +D₂2| + . . . = D_ii|

В качестве координат векторов состояния выступают амплитуды некоторых событий, а именно:

• каждое число типа S_i =i|Sпредставляет собой амплитуду перехода частицы из начального состояния |Sв базисное состояние прибора-анализатора с номеромi;

• каждое число типа D_i =D|iпредставляет собой амплитуду перехода частицы из базисного состояния прибора-анализатора с номеромiв конечное состояниеD|.

При таком подходе бра- и кет-векторы, а также их координаты кажутся принципиально различными по смыслу, но эта разница не абсолютна. Одно и то же состояние Rможно рассматривать и как начальное — |R, и как конечное —R|. Точка зрения на состояние зависит от способа его анализа. Например, можно представить себе две экспериментальные ситуации, "устроенные" одинаково в пространственном отношении, но отличающиеся направлением движения частиц. Состояния, обозначаемые буквамиS иD,выступают здесь и как начальные, и как конечные.

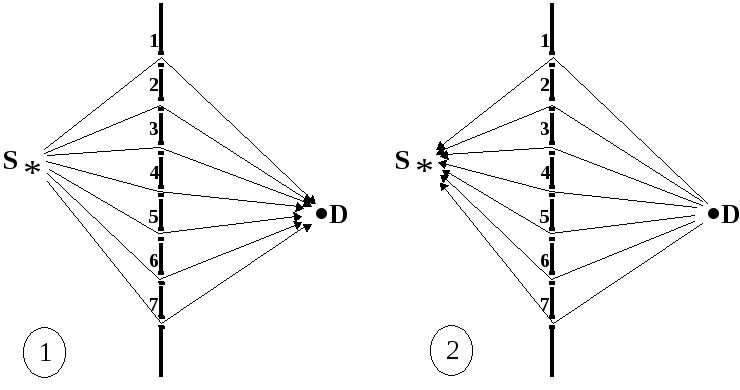
Перейти от ситуации (1) к ситуации (2) можно простым обращением знака пространственной (x) или временной (t) координаты, характеризующих перемещение частиц. При этом фаза каждой амплитуды изменит знак на противоположный:

 = kx=t–= –kx= –t

Следовательно, координаты вектора состояния, соответствующие этим двум ситуациям, будут отличаться только одним — комплексным сопряжением. Например, для состояния Sбудем иметь:

Ситуация 1: |S= |1S₁+ |2S₂+ . . . =|iS_i

 D | = D₁   1 | + D₂   2 | + . . . =  D_i   i |

Ситуация 2:  S | = S₁^*   1 | + S₂^*   2 | + . . . =  S_i^*   i |

| D  = | 1   D₁* + | 2   D₂* + . . . =  | i   S_i*

Таким образом, любое состояние достаточно проанализировать только одним из возможных способов. Если мы знаем, как выглядит бра-вектор некоторого состояния, то мы автоматически знаем, как выглядит и егокет-вектор, и наоборот. Для перехода отбра-вектора ккет-вектору и обратно достаточно поменять все знаки в фазах амплитуд-координат. Для такой операции, включающей одновременное преобразование типа вектора (строкастолбец) и комплексное сопряжение его координат, применяют термин "эрмитово сопряжение" или просто "сопряжение" (обозначается значком⁺ ). Таким образом, для любого состояния можно записать:

| S=S|⁺и S| = |S⁺

| D=D|⁺и D| = |D⁺

Отсюда можно заключить, что целесообразно использовать какую-то одну универсальную методику анализа векторов любых состояний. В основе такой методики лежит использование спектральных анализаторов.