Анализ векторов состояния

Пусть имеется частица, приготовленная в некотором определенном состоянии , которое нужно проанализировать и описать посредством векторной модели. Возьмем любой спектральный анализаторА и пропустим частицу через него. На выходе из прибора частица может оказаться в одном из вторичных пучков, т.е. перейти в некоторое определенное (по отношению к данному прибору) состояниеA_i. Проведя множество повторных испытаний, мы сможем установить вероятность попадания частицы в любой из вторичных пучков и приписать этим событиям (попаданиям) соответствующие амплитуды.

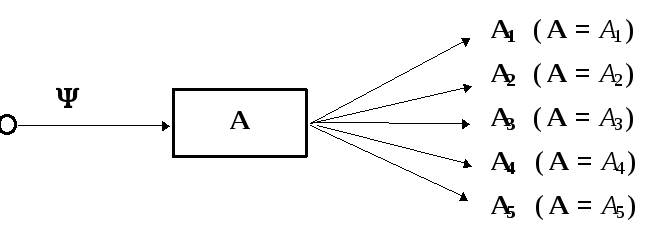
Будем рассматривать вторичные состояния, приготавливаемые прибором, как базисные. Тогда исходное состояние можно трактовать как суперпозицию (ЛК) базисных состояний:

| =а₁|А₁+а₂|А₂+ . . . =а_i |А _i

где в качестве координат выступают амплитуды:

а_i =А_i|

Важным преимуществом такого подхода является то, что базисным состояниям и соответствующим амплитудам можно придать вполне определенный физический смысл:

• каждое базисное состояние отличается тем, что в нем наблюдаемая Аимеет точно определенное значение (А=А_i),

• координата вектора с номеромi (а_i) представляет собой амплитуду того, что при измерении наблюдаемойАбудет найдено ее допустимое значение с тем же номеромi (А_i ), квадрат данной амплитуды представляет собой соответствующую вероятность: |а_i |²=P_i.

Очевидно, что после прохождения прибора частица неизбежно попадет в один из вторичных пучков. Поэтому сумма вероятностей по всем вторичным пучкам будет обязательно равна 1:

| а₁ |²+ |а₂ |²+ . . . = |а_i |² = 1

В математике векторы, для которых выполняется такое условие (сумма квадратов координат равна 1), называются нормированными. Отсюда можно заключить, что все квантово-механические векторы состояния должны быть нормированными. Только в этом случае можно трактовать координаты вектора как амплитуды переходов в базисные состояния некоторого прибора, а их квадраты — как вероятности обнаружения соответствующих допустимых значений наблюдаемой.

Представления векторов состояния

Спектральных анализаторов, предназначенных для измерения наблюдаемых, существует много. Очевидно, что для анализа некоторого состояния мы можем воспользоваться любым из них. В каждом конкретном случае мы будем получать свой набор амплитуд-координат.

Прибор А:

| = |А₁а₁+ |А₂а₂+ ... = |А_i а_i , гдеа_i =А_i|

Прибор B:

| = |B₁b₁+ |B₂b₂+ ... = |B_ib_i , гдеb_i =B_i|

Прибор C:

|   = | C₁   c₁ + | C₂   c₂ + ... =  | C_i   c_i , где c_i =  C_i |  

Такие различные изображения одного и того же состояния, получаемые посредством различных приборов, называются представлениями.Другими словами, каждый вектор состояния может иметь множество различных представлений. Эти представления относятся к разным наборам базисных состояний (приборам) и поэтому характеризуются различными совокупностями амплитуд-координат.

Различие между представлениями вектора состояния точно такое же, как между представлениями геометрических векторов в различных системах координат. Так, на плоскости можно ввести множество координатных систем, причем координаты одного и того же вектора в разных системах будут различными:

Очевидно, что мы можем изобразить вектор Rдвояким способом:

R = R_x + R_y = x  i + y  j = ( x, y ) ( в базисе i, j )

R = R_f + R_g = f  f + g  g = ( f, g ) ( в базисе f, g )

Два разных набора чисел дают нам представление об одном и том же векторе, но с разных точек зрения. Следует обратить внимание на следующий факт: как один набор чисел — (x,y), так и другой — (f,g), дают нам определенные сведения о вектореR. Эти два набора чисел содержат одну и ту же информацию, они взаимозаменяемы, а не взаимодополняемы. Если нам известны два базиса, то координаты вектора, определенные по отношению к этим базисам, можно пересчитывать друг в друга без потери (но и без приобретения) информации.

Так, например, для двух декартовых координатных систем на плоскости, повернутых относительно друг друга на угол , действует правило:

Взаимно обратные матрицы, посредством которых один вектор-столбец (или вектор-строка) преобразуется в другой, называются "операторами преобразования координат".

Точно такая же ситуация имеет место и в квантовой механике. Мы можем анализировать одно и то же состояние с помощью разных приборов и получать в результате различные наборы координат. Каждый такой набор содержит исчерпывающую информацию о состоянии объекта. Представления, полученные с помощью разных приборов, могут быть однозначно преобразованы друг в друга с помощью матриц (операторов преобразования координат), которые в квантовой механике называются унитарными операторами.Такие операторные преобразования играют роль механических уравнений состояния, связывающих значения различных, но зависимых друг от друга наблюдаемых.