
Лекции / семестр3 / Альшина (МП-2) / Pr5
.doc§9. Ряды комплексных чисел.
-
Числовые ряды.
Пусть дана последовательность {an} комплексных чисел.
Определение.
Бесконечная сумма членов последовательности
называется
![]() рядом.
рядом.
Определение.
Конечные суммы Sn=![]() называются частичными
суммами
ряда.
называются частичными
суммами
ряда.
Они также образуют последовательность {Sn}.
Определение.
Числовой ряд называется сходящимся,
если сходится последовательность его
частичных сумм {Sn}S.
Предел последовательности частичных
сумм называется суммой
ряда
![]() =S.
=S.
Определение.
Ряд
![]() -
остаток
ряда.
Очевидно
-
остаток
ряда.
Очевидно
![]() .
Остаток сходящегося ряда –
число.
Будем обозначать его rn.
.
Остаток сходящегося ряда –
число.
Будем обозначать его rn.
Пример.
Сумма бесконечной геометрической
прогрессии
![]() - простейший пример ряда. Последовательность
частичных сумм этого ряда
- простейший пример ряда. Последовательность
частичных сумм этого ряда
![]() .
При q<0
этот ряд сходится и
.
При q<0
этот ряд сходится и
![]() .
.
2. Свойства сходящихся рядов.
Необходимый
признак сходимости ряда.
Если
![]() сходится, то an0
.
сходится, то an0
.
Доказательство. У сходящегося ряд сходится последовательность частичных сумм {Sn} >0 N( ): |Sn+m-Sn|<для n>N и m>0 |an+1|=|Sn+1-Sn|<для n>N an0 при n.
Теорема
9.1. Пусть c
– комплексное число. Если ряд
![]() сходится, то и ряд
сходится, то и ряд
![]() также
сходится и
также
сходится и
![]() .
.
Доказательство.
Рассмотрим
частичные суммы
![]() и
и
![]() .
По условию
.
По условию ![]() .
Т.к.
Sn=cS’n
и
.
Т.к.
Sn=cS’n
и
![]() =
=![]() .
Согласно определению суммы ряда отсюда
сразу следует
.
Согласно определению суммы ряда отсюда
сразу следует
![]() .
.
Теорема
9.2.
Пусть ряды
![]() и
и
![]() сходятся, тогда ряд
сходятся, тогда ряд
![]() также сходится и
также сходится и
![]() =
=![]() +
+![]() .
.
Доказательство.
Рассмотрим частичные суммы
![]() ,
,
![]() и
и
![]() .
Очевидно, n=Sn+S’n.
По условию
.
Очевидно, n=Sn+S’n.
По условию ![]() и
и
![]()
![]() =
=
![]() +
+![]() .
Откуда сразу следует утверждение
теоремы.
.
Откуда сразу следует утверждение
теоремы.
Пример.
![]() =
=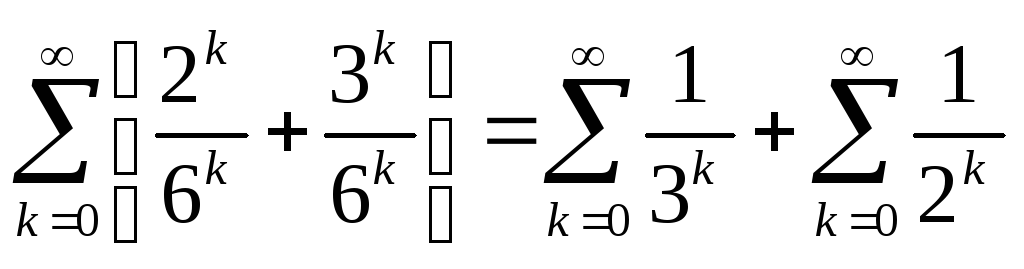 =
=![]() .
.
3. Критерий Коши сходимости ряда.
Для числовых последовательностей существует необходимый и достаточный признак сходимости. {Sn} сходится >0 N(): |Sn+m-Sn|<для n>N и m>0. Отсюда следует
Критерий
Коши сходимости ряда:
Для
сходимости ряда
![]() необходимо и достаточно, чтобы >0
N():
|an+an+1+…+an+m|<для
n>N
и m
необходимо и достаточно, чтобы >0
N():
|an+an+1+…+an+m|<для
n>N
и m![]() 0.
0.
Пример.
Рассмотрим гармонический
ряд
-
![]() .
.
n>0
m=n-1
![]() =
=![]() >
>![]() .
.
Таким образом, для n>0 при =0.5 и m=n-1 критерий Коши не выполняется.
§10 Признаки сходимости рядов с неотрицательными членами.
-
Основные понятия.
Определение.
Если ряд из модулей
![]() сходится, то ряд исходный ряд
сходится, то ряд исходный ряд
![]() называется абсолютно
сходящимся.
называется абсолютно
сходящимся.
Теорема 10.1. Если ряд сходится абсолютно, то он сходится в обычном смысле.
Доказательство.
Если
ряд из модулей![]() сходится, то для него выполнен критерий
Коши
>0
N():
сходится, то для него выполнен критерий
Коши
>0
N():
![]() <
для n>N
и m
<
для n>N
и m![]() 0,
но |an+an+1+…+an+m|
0,
но |an+an+1+…+an+m|![]() <для
исходного ряда также выполнен критерий
Коши
и он
сходится.
<для
исходного ряда также выполнен критерий
Коши
и он
сходится.
Обратное, вообще говоря, неверно.
Определение. Если сам ряд сходится, а соответствующий ряд из модулей расходится, то ряд называется условно сходящимся.
Из свойств неубывающих последовательностей
Лемма.
Для того, чтобы ряд с неотрицательными
членами сходился необходимо и достаточно,
чтобы последовательность его частичных
сумм была бы ограниченна сверху, причем,
если S=sup{![]() },
то S
– сумма
ряда.
},
то S
– сумма
ряда.
Пример.
![]()
![]() =
=
![]()
Т.о. у ряда с положительными членами ограничена последовательность частичных сумм ряд сходится.
2. Признаки сравнения для рядов с неотрицательными членами.
Теорема 10.2. (Первый признак сравнения) Пусть an 0, bn 0 и an =O(bn). Тогда
-
если ряд
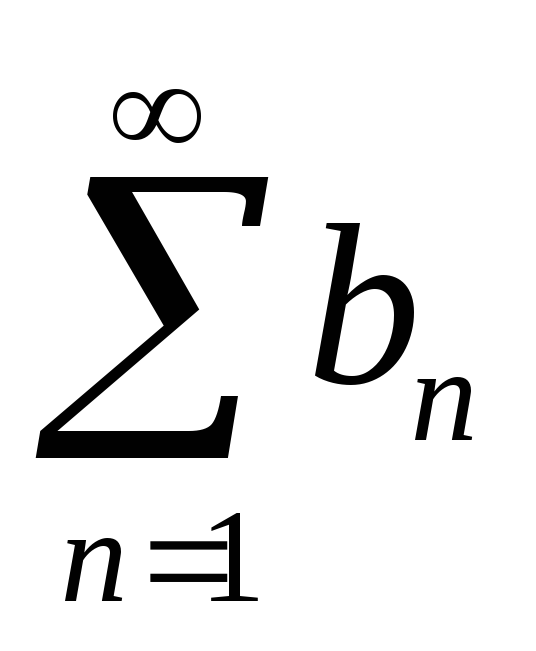 сходится, то сходится и ряд
сходится, то сходится и ряд
 ;
;
-
если же расходится ряд
 ,
то расходится и ряд
,
то расходится и ряд
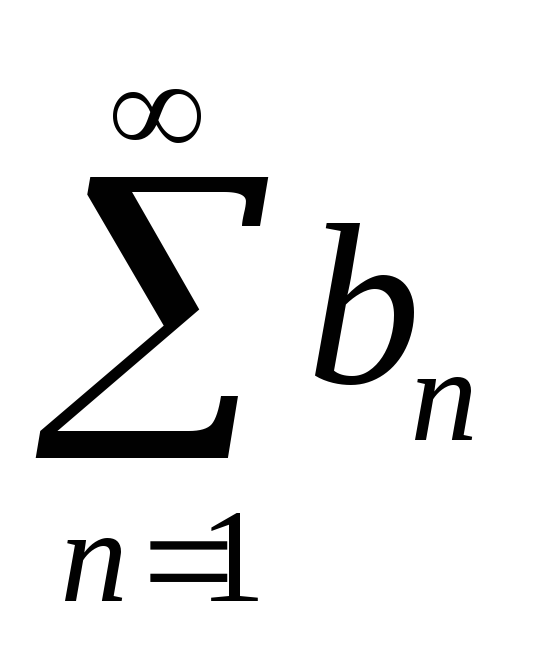 .
.
Доказательство.
По определению an =O( bn) 0<c< : an c bn, в частности возможно an bn.
-
если “больший” ряд
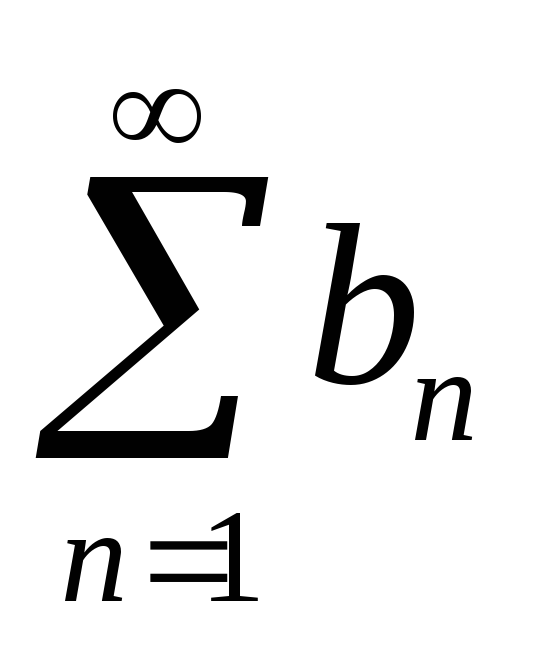 сходится
ограничена последовательность его
частичных сумм
сходится
ограничена последовательность его
частичных сумм
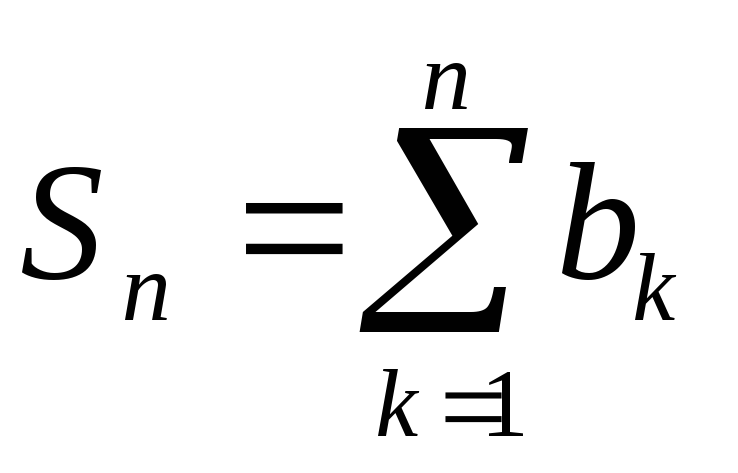
M<,
но тогда последовательность частичных
сумм “меньшего”
ряда
M<,
но тогда последовательность частичных
сумм “меньшего”
ряда
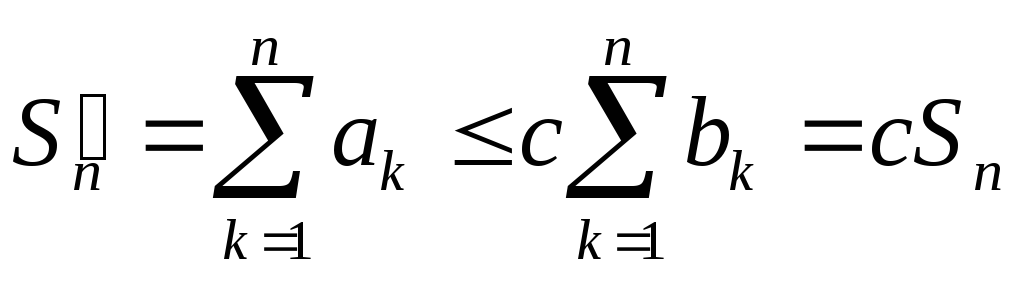 cM
также ограничена сверху.
Тогда по
Лемме
ряд
cM
также ограничена сверху.
Тогда по
Лемме
ряд
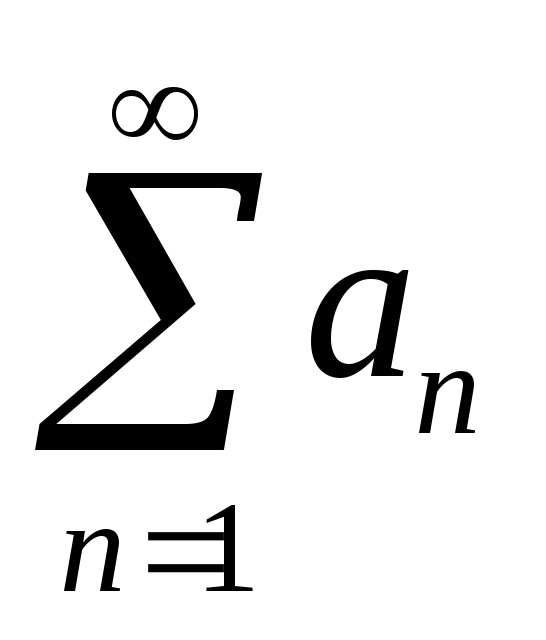 сходится.
сходится. -
Предположим обратное, а именно “больший” ряд
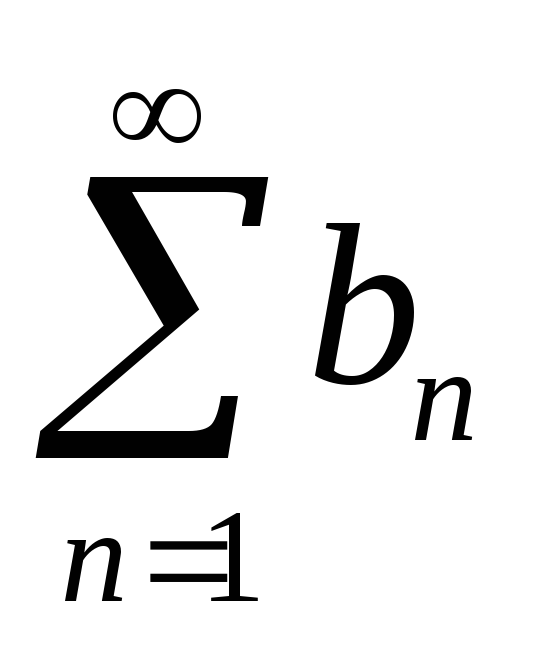 сходится, тогда по доказанному в п.1)
“меньший”
ряд
сходится, тогда по доказанному в п.1)
“меньший”
ряд
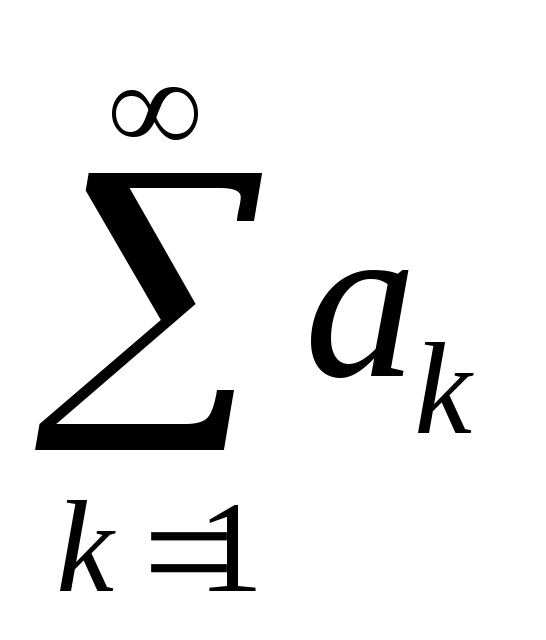 должен сходится, а это противоречит
условию.
должен сходится, а это противоречит
условию.
Теорема
10.3. (Второй
признак сравнения)
Пусть an
>0,
bn
>0
и
![]() ,
0<k<.
Тогда ряды
,
0<k<.
Тогда ряды
![]() и
и
![]() сходятся
или расходятся одновременно.
сходятся
или расходятся одновременно.
Доказательство.
Если
![]() ,
то >0
N():
n>N()
,
то >0
N():
n>N()

![]()
![]() Выбирая
,
можем добиться k->0.
Применяя первый
признак сравнения
и оценку
Выбирая
,
можем добиться k->0.
Применяя первый
признак сравнения
и оценку
![]() ,
получим, что из сходимости ряда
,
получим, что из сходимости ряда
![]() следует сходимость ряда
следует сходимость ряда
![]() .
Аналогично используя оценку
.
Аналогично используя оценку
![]() ,
из расходимости ряда
,
из расходимости ряда
![]() следует рассходимость ряда
следует рассходимость ряда
![]() .
.
Примеры.
-
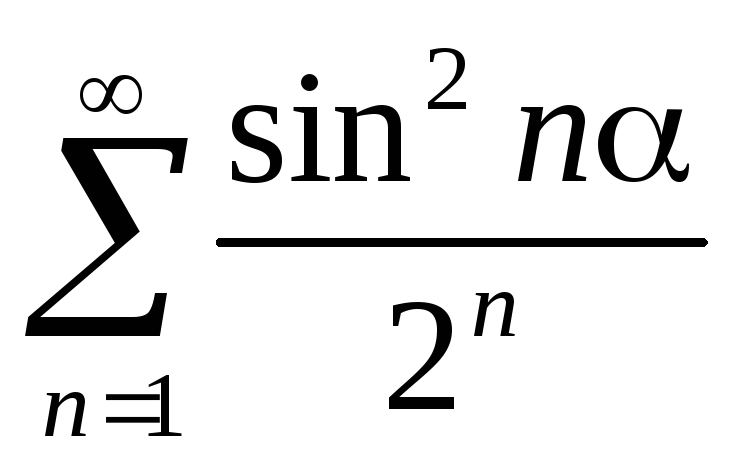 ,
,
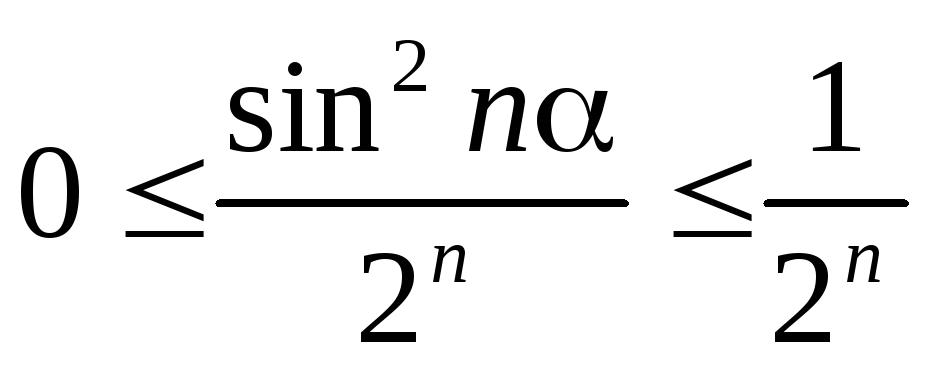 ,
а ряд
,
а ряд
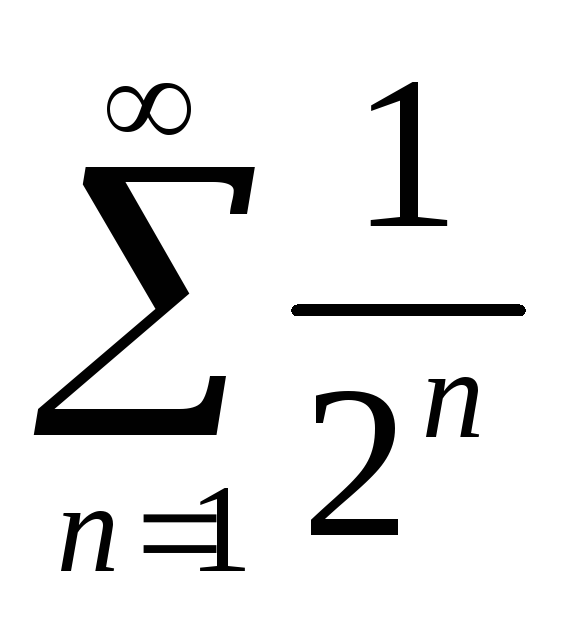 сходится – это сумма бесконечно
убывающей геометрической прогрессии.
сходится – это сумма бесконечно
убывающей геометрической прогрессии. -
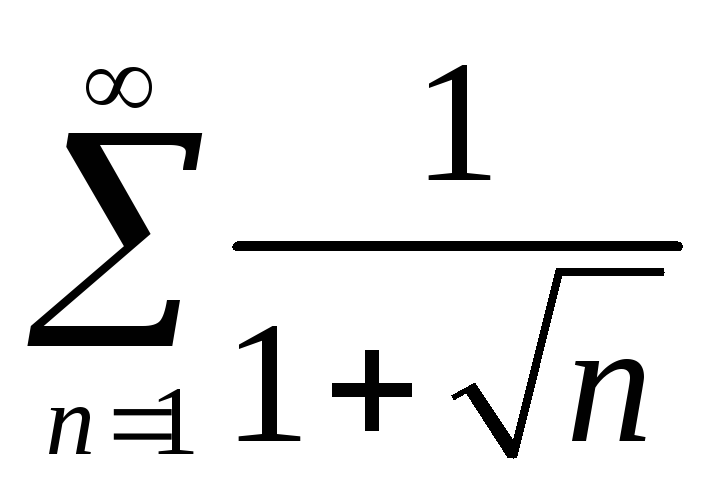 ,
начиная с определенного номера n>N
выполнено
,
начиная с определенного номера n>N
выполнено
 ,
а гармонический ряд
,
а гармонический ряд
 расходится
расходится и исходный ряд.
расходится
расходится и исходный ряд. -
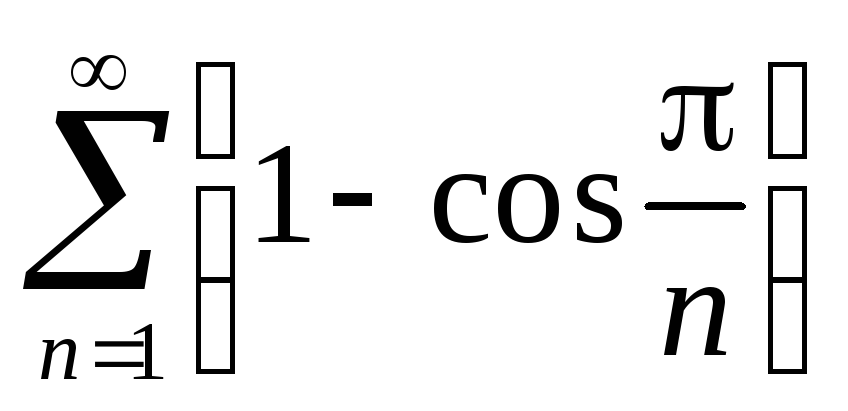 -
ряд с неотрицательными членами.
-
ряд с неотрицательными членами.
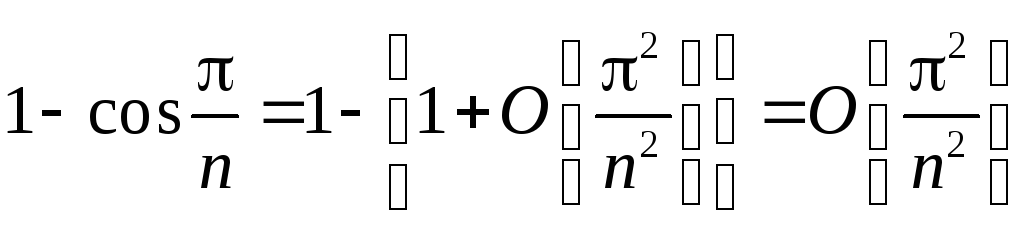 при
n.
при
n.
Но
ряд
![]() сходится, значит по первому признаку
сравнения сходится и исходный ряд.
сходится, значит по первому признаку
сравнения сходится и исходный ряд.
-
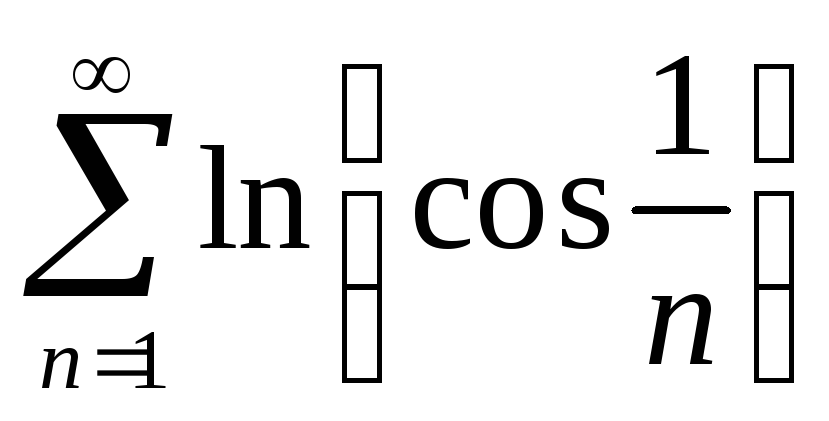 -
ряд с отрицательными членами, но если
мы докажем сходимость ряда
-
ряд с отрицательными членами, но если
мы докажем сходимость ряда
 ,
то мы тем самым докажем сходимость
исходного ряда.
,
то мы тем самым докажем сходимость
исходного ряда.
 при n
исходный ряд сходится.
при n
исходный ряд сходится. -
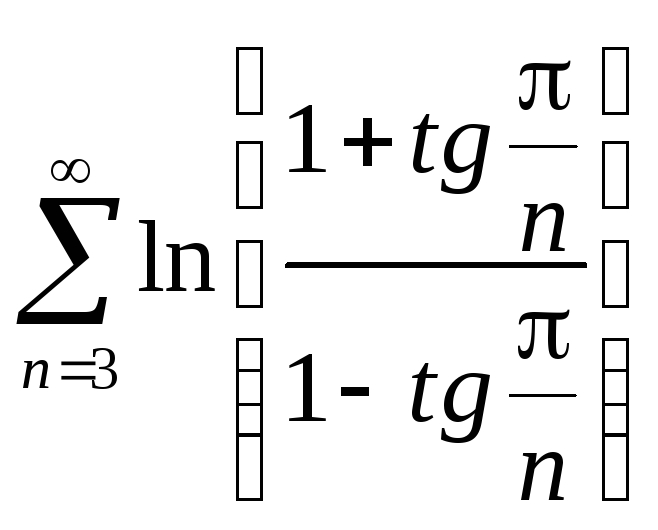 -
ряд с положительными членами, т.к.
-
ряд с положительными членами, т.к.
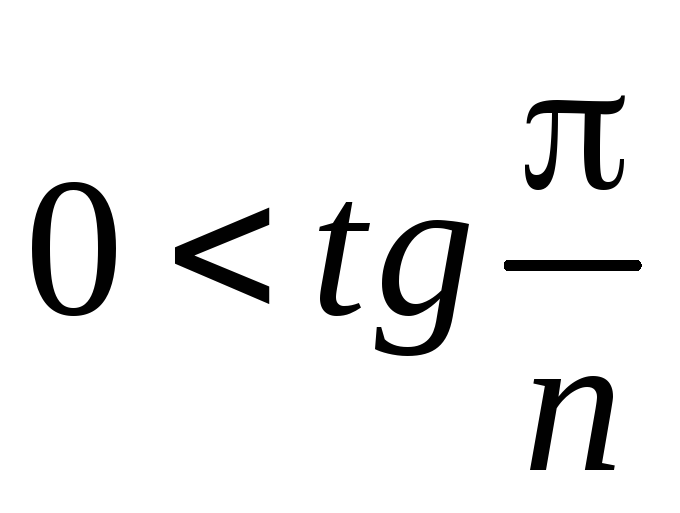 при n=3,4,…
и
при n=3,4,…
и
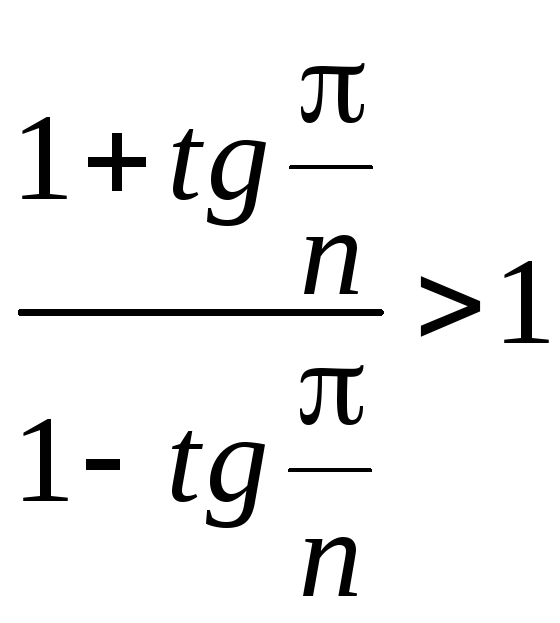 (под
логарифмом стоит число, большее единицы).
Учитывая, что
(под
логарифмом стоит число, большее единицы).
Учитывая, что
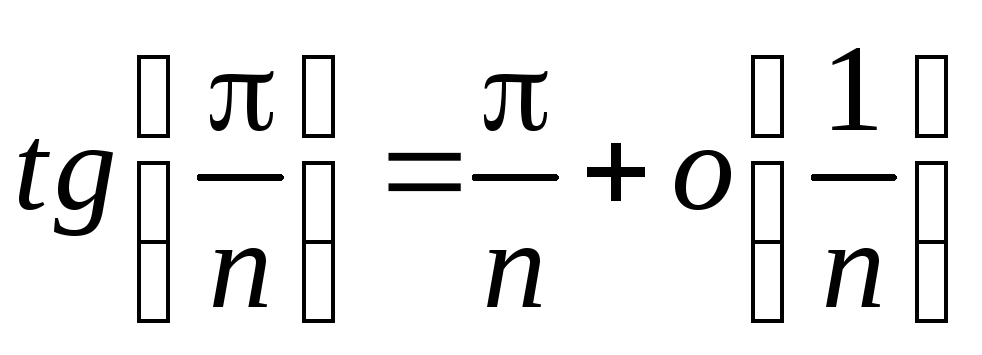 при n,
получим асимптотику членов исходного
ряда
при n,
получим асимптотику членов исходного
ряда
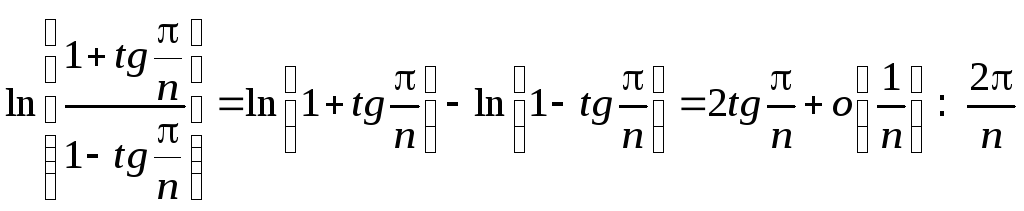 ,
,
т.о. исходный ряд эквивалентен гармоническому и расходится.
