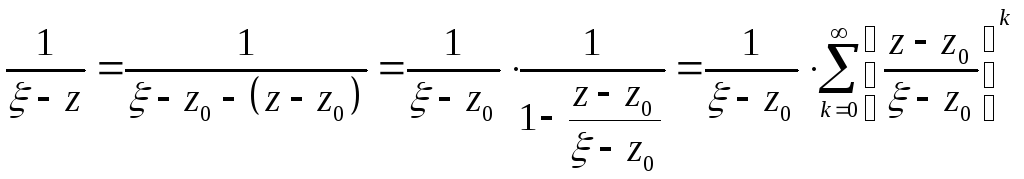Лекции / семестр3 / Альшина (МП-2) / Pr9
.doc§15. Степенные ряды.
Определение. Степенным рядом назовем ряд вида cn(z-z0)n, z0 -центр, cn - коэффициенты - заданные комплексные числа. При z= z0 ряд очевидно сходится. Это может быть единственная точка сходимости n!zn, а также ряд может сходится на всей комплексной плоскости zn/n!. При исследовании степенного ряда важно установить область его равномерной сходимости. Как будет показано далее, область сходимости степенного ряда определяется видом его коэффициентов cn.
-
Теорема Абеля.
Теорема Абеля. Если степенной ряд cn(z-z0)n сходится в точке z1 z0 , то он абсолютно сходится и при z: |z-z0|<|z1-z0 |, причем в замкнутом круге
|z-z0|<|z1-z0| сходится равномерно. Доказательство. Выберем произвольную точку z: |z-z0|<|z1-z0|. В силу необходимого условия сходимости ряда A>0 : для n |cn(z1-z0)n|<A
|cn|<A/|z1-z0|n |cn(z-z0)n|<A|(z-z0)/(z1-z0)|n .
Но |(z-z0)/(z1-z0)|=q<1 |cn(z-z0)n|<Aqn ряд мажорируется бесконечно убывающей геометрической прогрессией сходится абсолютно.
При |z-z0| <|z1-z0| ряд сходится равномерно по мажорантному признаку Вейерштрасса т.к. |cn(z-z0)n| A|/(z1-z0)|n < Aqn , q<1
Следствия теоремы Абеля. 1. Если степенной ряд расходится в точке z2 z0 , то он расходится и при z: |z-z0|>|z2-z0 |. (Предполагая противное, получим, что по тереме Абеля ряд должен сходится в круге радиуса <|z-z0 |, в частности и в точке z2, что противоречит условию.). 2. Круг сходимости. Радиус сходимости. Рассмотрим sup|z1-z0 |=R для z1, где ряд сходится - точную верхнюю грань расстояний от точки z0 до точек z1, в которых сходится ряд cn(z-z0)n .
Если R, то для z2: |z2-z0|>R ряд расходится. R=inf|z2-z0 |=R для z2 , где ряд расходится. Пусть R>0, тогда наибольшей областью сходимости степенного ряда является круг |z-z0|<R - круг сходимости степенного ряда, число R>0 - радиус сходимости степенного ряда. Внутри круга сходимости ряд сходится, вне - расходится, в точках границы |z-z0|=R может как сходиться, так и расходиться.
3.Формула Коши-Адамара.
R=1/L,
L=![]()
Доказательство.
Применяем радикальный признак Коши
![]()
Пусть сначала 0<L<,
Тогда
ряд сходится при
![]()
Если L=0, то
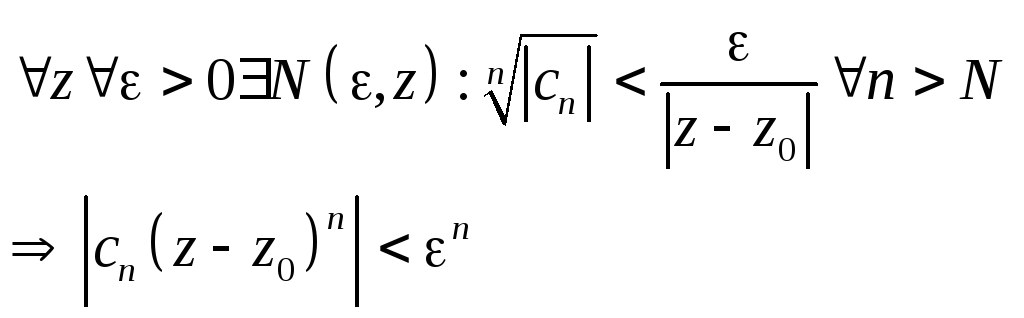
т.о.
члены ряда мажорируются членами
бесконечно убывающей геометрической
прогрессии, следовательно ряд сходится
![]() ,
и формально можно записать для радиуса
сходимости
,
и формально можно записать для радиуса
сходимости
![]()
Если L=, то
![]()
т.о.
существует бесконечно много членов
ряда, больших 1, т.о. не выполнен необходимый
признак сходимости рядов, т.е. ряд
рассходится
![]() ,
и формально можно записать для радиуса
сходимости
,
и формально можно записать для радиуса
сходимости
![]()
4. В круге |z-z0|<R степенной ряд сходится равномерно. => По теореме Вейерштрасса cn(z-z0)n=f(z)C(|z-z0|<R).
5. По теореме Вейерштрасса степенной ряд внутри круга сходимости можно дифференцировать и интегрировать почленно любое число раз. При этом радиус сходимости не меняется!
6. cn(z-z0)n=f(z) c0=f(z0), cn+1(n+1)(z-z0)n=f '(z) c1=f '(z0)… cn+k(n+k)!(z-z0)n=f(k)(z) ck=f(k)(z0)/k!
7.
Пример.
![]() : cn=1
R=1.
: cn=1
R=1.
Sn=[1-(z-z0)n+1]/[1-(z-z0)]; |z-z0 |<1
![]() =1/[1-(z-z0)].
=1/[1-(z-z0)].
![]() =1/[1-(z-z0)]-
Формула суммы бесконечной геометрической
прогрессии.
=1/[1-(z-z0)]-
Формула суммы бесконечной геометрической
прогрессии.
8. Сходимость ряда на границе требует дополнительного исследования
-
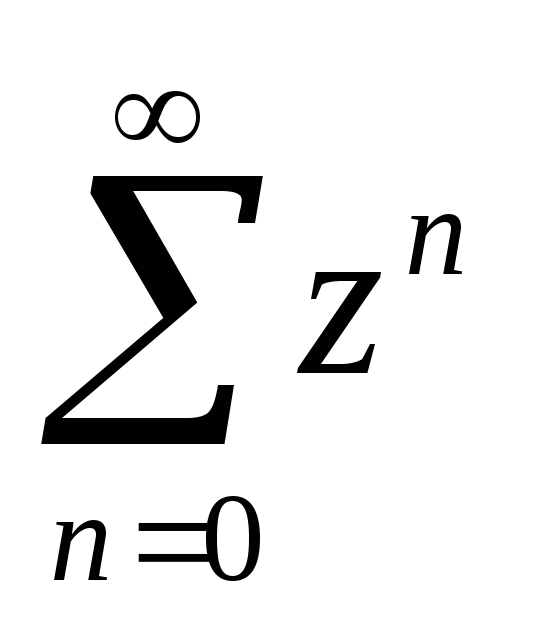 по
формуле Коши-Адамара R=1,
на границе круга сходимости нет, т.к.
модуль членов ряда не убывает ни для
каких z.
по
формуле Коши-Адамара R=1,
на границе круга сходимости нет, т.к.
модуль членов ряда не убывает ни для
каких z. -
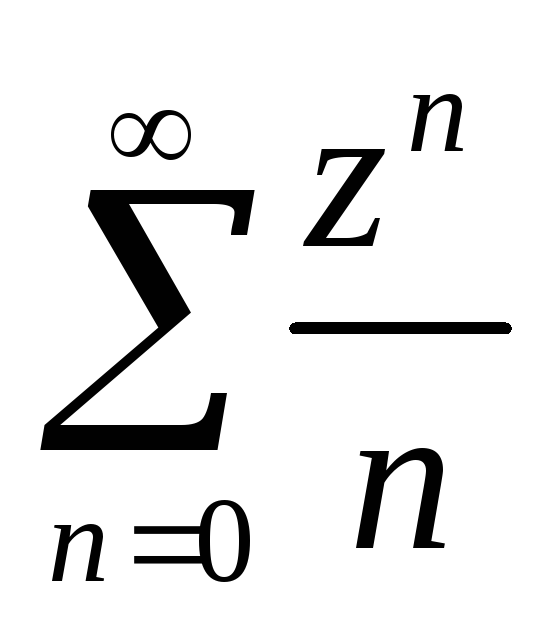 по
формуле Коши-Адамара R=1,
в некоторых точках границы круга ряд
сходится (z=-1
по
формуле Коши-Адамара R=1,
в некоторых точках границы круга ряд
сходится (z=-1
 ),
а в других расходится (z=1
),
а в других расходится (z=1
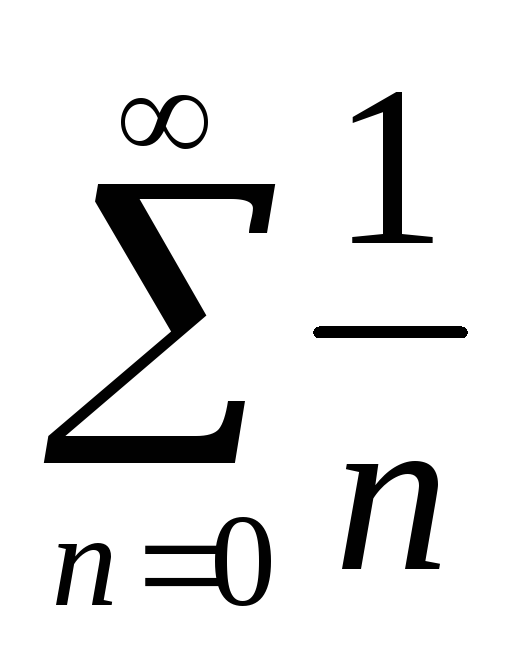 ),.
),. -
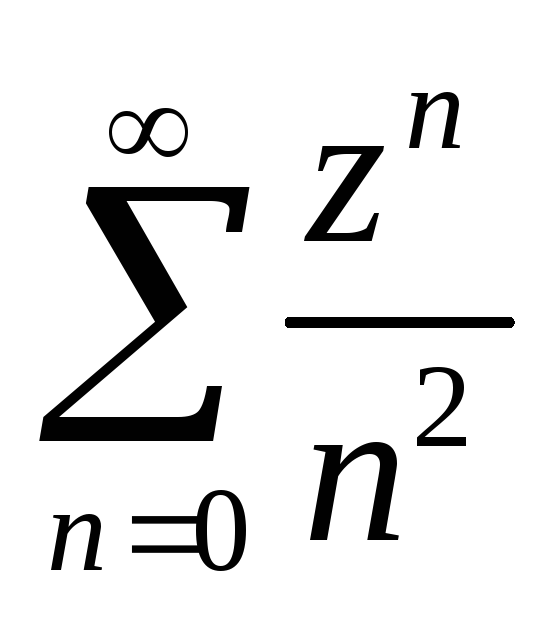 по
формуле Коши-Адамара R=1,
на границе круга ряд сходится, т.к.
мажорируется сходящимся
по
формуле Коши-Адамара R=1,
на границе круга ряд сходится, т.к.
мажорируется сходящимся
 .
.
9. Вторая теорема Абеля. Если степенной ряд сходится и на границе круга сходимости, то сходимость равномерная внутри всего замкнутого круга сходимости.
(очевидность следует из мажорантного признака Вейерштрасса)
Итак cn(z-z0)n=f(z)C(|z-z0|<R). Можно ли функции, аналитической внутри некоторого круга, сопоставить степенной ряд, сходящийся в этом круге к данной функции?
Ответ на этот вопрос дает
-
Теорема Тейлора.
Теорема Тейлора. Если f(z)C(|z-z0|<R), то степенной ряд
cn(z-z0)n =>f(z) при |z-z0|<R.
|
|
Доказательство. Возьмем z: |z-z0|<R и построим C - окружность радиуса с центром в точке z0 и содержащую точку z внутри: для C: | -z0|=, <R, |-z0|>|z-z0|. Т.к. f(z)C(|z-z0|< ), то по интегральной формуле Коши
Преобразуем подынтегральное выражение
Мы воспользовались формулой суммы бесконечно убывающей геометрической прогрессии, ведь |z-z0|/|-z0|<1. |
C
ряд сходится
равномерно по так
как мажорируется сходящимся числовым
рядом

f(z)=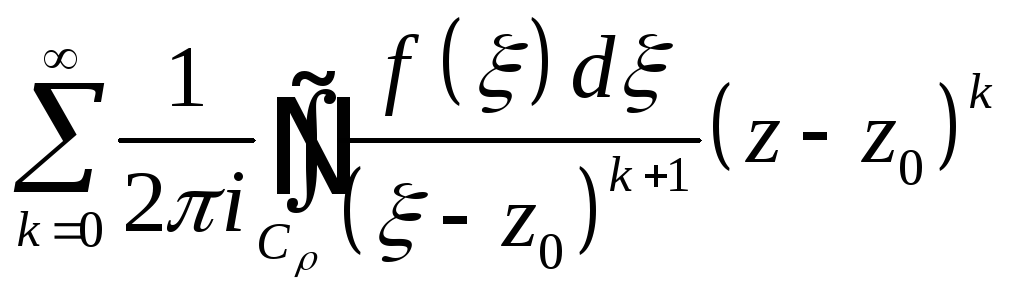
![]() ;
;
cn=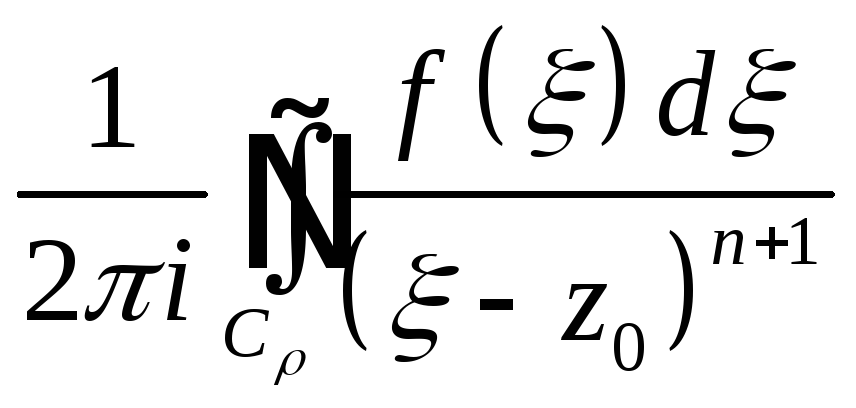 =f(n)(z0)/n!,
что и доказывает и
единственность разложения.
=f(n)(z0)/n!,
что и доказывает и
единственность разложения.
Замечания 1) Разложение функции f(z)= cn(z-z0)n называют разложением функции в ряд Тейлора.
2)
По теореме Коши cn=
 ,
где C - произвольный кусочно-гладкий
контур, содержащий внутри себя точку
z0,
целиком лежащий в области аналитичности
функции.
,
где C - произвольный кусочно-гладкий
контур, содержащий внутри себя точку
z0,
целиком лежащий в области аналитичности
функции.
Пример.
![]()
![]() ;
;
![]() …
…

 .
.
-
Ряды Тейлора элементарных функций.
-
 (Воспользоваться
(Воспользоваться
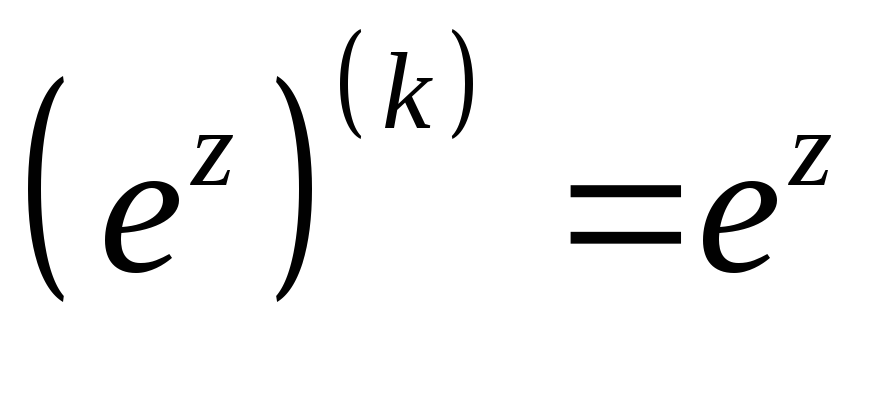
k
Ck=1/k!)
k
Ck=1/k!) -
 (Воспользоваться
(Воспользоваться
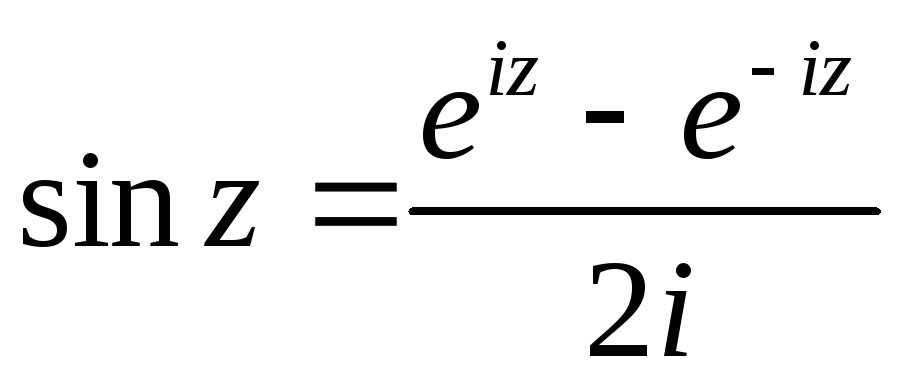 )
) -
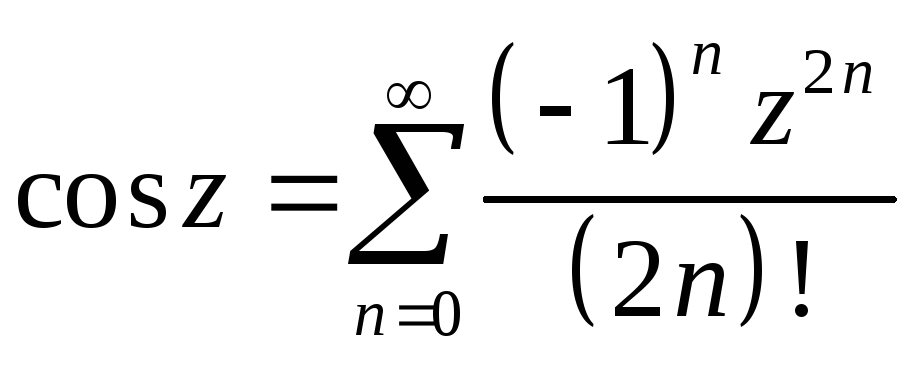 (Воспользоваться
(Воспользоваться
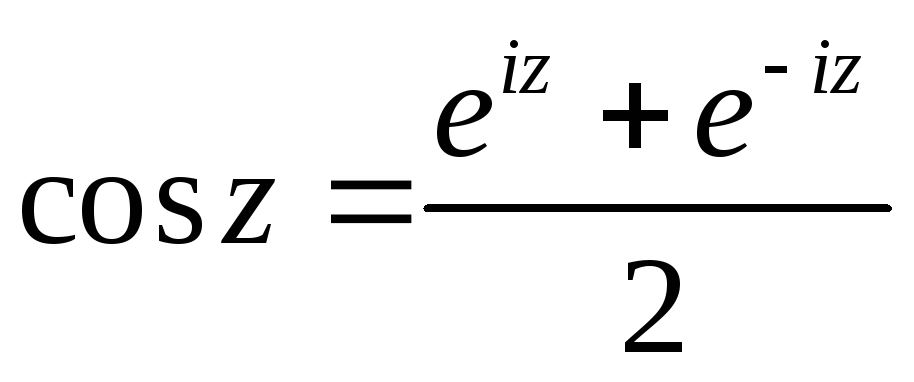 )
) -
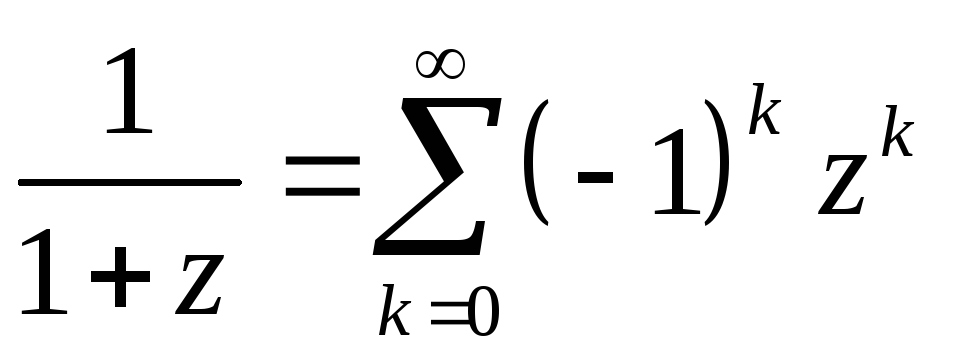 ,
,
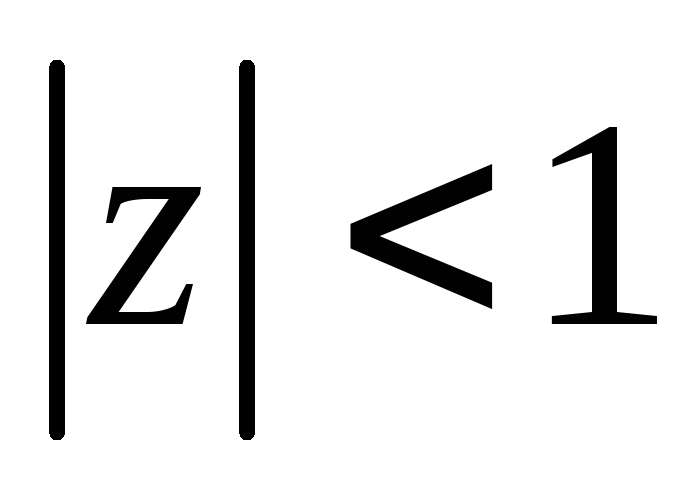 (Сумма
бесконечно убывающей геометрической
прогрессии)
(Сумма
бесконечно убывающей геометрической
прогрессии) -

 (Воспользоваться
тем, что производная данной функции
может быть представлена суммой бесконечно
убывающей геометрической прогрессии
(Воспользоваться
тем, что производная данной функции
может быть представлена суммой бесконечно
убывающей геометрической прогрессии
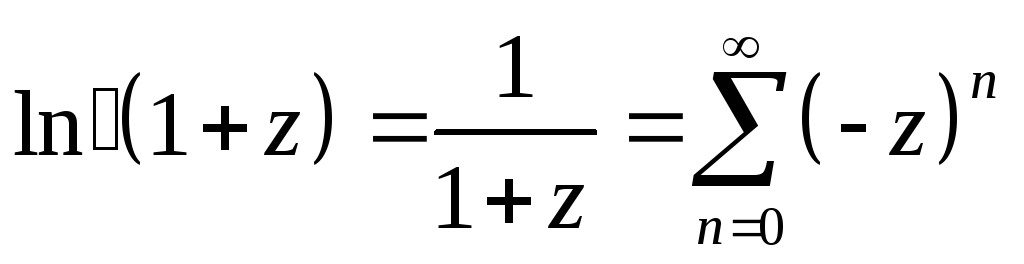 ,
ряд для
исходной функции получается почленным
интегрированием ряда для производной)
,
ряд для
исходной функции получается почленным
интегрированием ряда для производной) -

 (Воспользоваться
тем, что производная данной функции
может быть представлена суммой бесконечно
убывающей геометрической прогрессии
(Воспользоваться
тем, что производная данной функции
может быть представлена суммой бесконечно
убывающей геометрической прогрессии
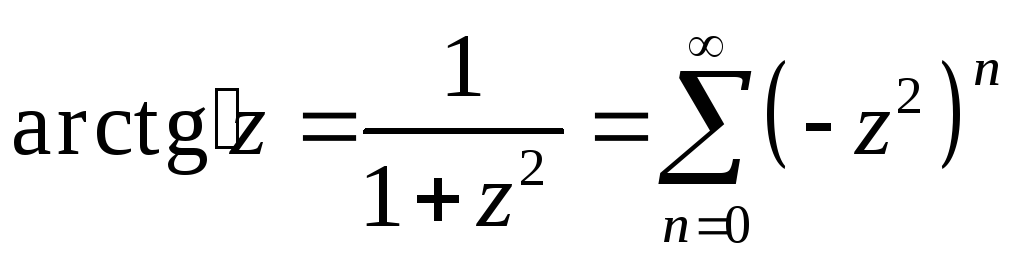 ,
ряд для
исходной функции получается почленным
интегрированием ряда для производной)
,
ряд для
исходной функции получается почленным
интегрированием ряда для производной) -

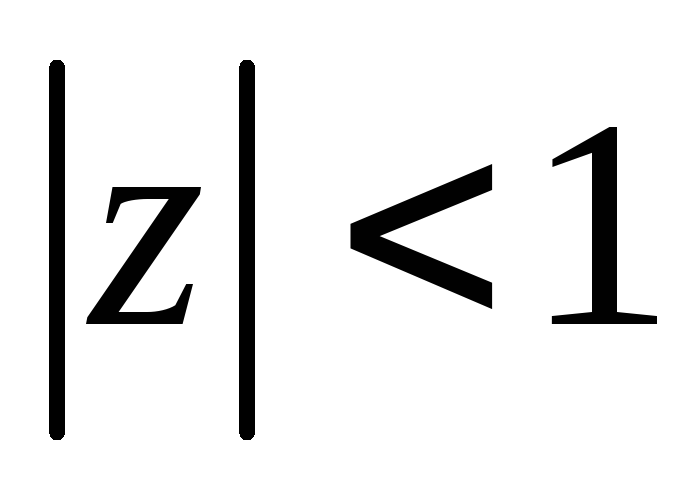
![]()
k
![]()
В
частности, при =0.5
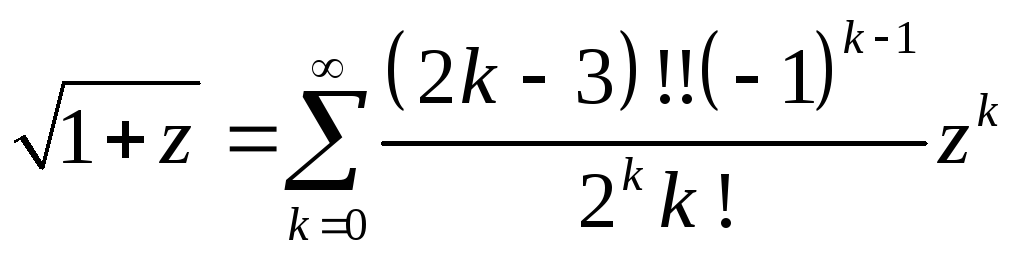

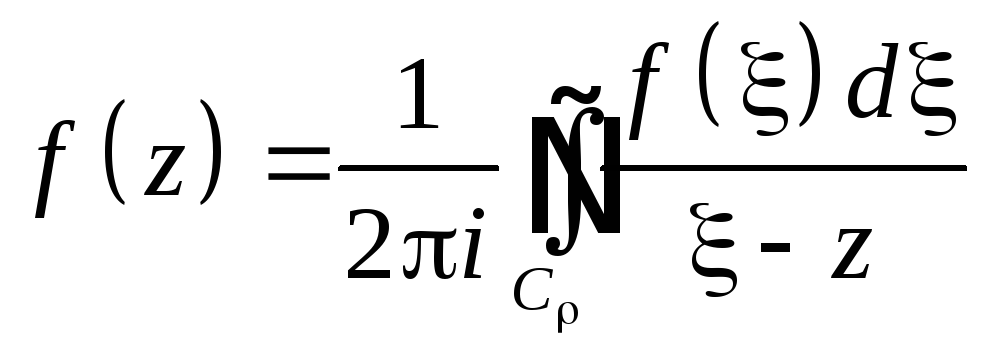 ;
;