Лекции / семестр3 / Альшина (МП-2) / Pr7
.doc§11. Знакопеременные ряды.
Определение.
Пусть
an0,
тогда ряд
- знакопеременный
ряд.
Теорема
Лейбница.
Если
и
,
то знакочередующийся ряд
сходится. При этом
n
- модуль n-ого
остатка ряда не превышает модуля
следующего члена ряда.
Доказательство.
Рассмотрим частичные суммы ряда четного порядка
Их можно записать в виде
,
здесь
каждая скобка неотрицательна, т.о.
последовательность частичных сумм
четного порядка не убывает.
Заметим, что ту же последовательность можно записать и так
Т.е. неубывающая последовательность ограничена сверху она сходится,
.
Покажем, что последовательность частичных сумм нечетного порядка стремится к тому же пределу. Действительно,
и
Отметим, что для знакопеременного ряда справедливо S2k S S2k+1 . Так как { S2k } – неубывающая последовательность, а { S2k+1 } – невозрастающая последовательность. Обе сходятся к своей верхней (нижней) грани.
S - S2k S2k+1 - S2k =a2k+1
и S2k-1 -S S2k-1 - S2k =a2k
.
Пример.
-
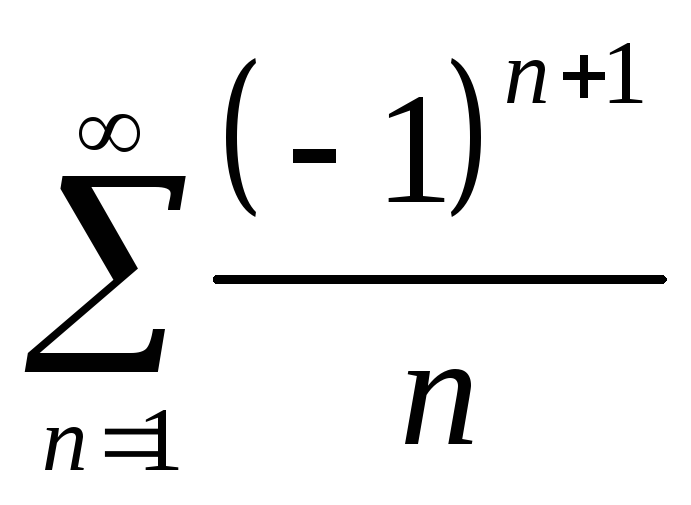сходится в силу признака Лейбница. И
его сумма
.
Причина противоречия состоит в том, что не все свойства сумм переносятся на ряды. В частности, слагаемые можно переставлять только в абсолютно сходящихся рядах.
§12. Абсолютно и условно сходящиеся ряды.
Примеры.
- сходится абсолютно.
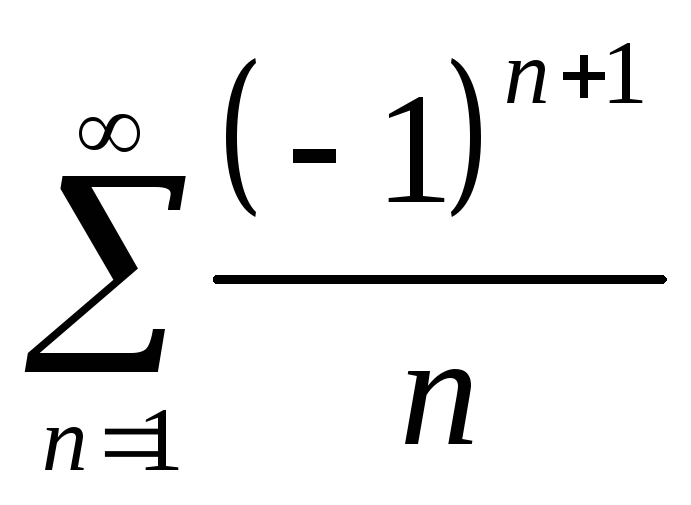- сходится условно.
Рассмотрим
произвольный ряд из комплексных чисел
.
Обозначим
- ряд, составленный из тех же чисел,
взятых в другом порядке
Теорема
12.1. Если ряд
- сходится абсолютно, то и
- так же сходится и имеет ту же сумму.
Члены абсолютно сходящегося ряда можно переставлять.
Доказательство.
Обозначим
,
,
.
Если
исходный ряд сходится абсолютно, то
-
предел неубывающей последовательности
частичных сумм
.
Зафиксируем произвольное >0. N:
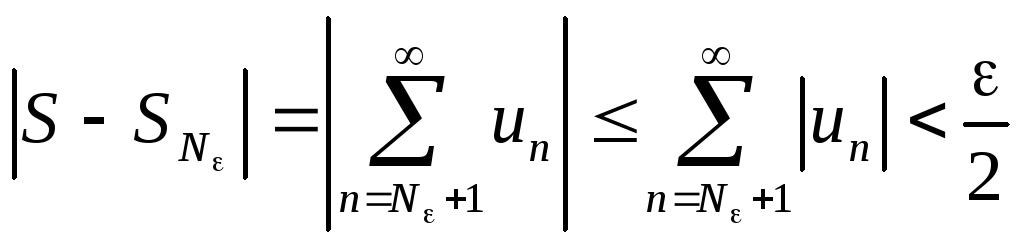
Выберем
такой большой номер M
такой, что частичная сумма
содержала бы все слагаемые, что и
.
Для
mM
обозначим
.
не
превышает суммы модулей своих слагаемых.
Т.к. номера этих слагаемых больше, чем
N,
то все они содержатся в сумме
.
Т.о. mM
т.е.
.
Замечание.
Более того ряд
сходится абсолютно.
Теорема
Риммана.
Если ряд
,
сходится условно, то
можно так переставить члены ряда, чтобы
сумма его была бы равна A!!!
Доказательство.
В
последовательности {an}
есть как положительные, так и отрицательные
члены. Выделим две подпоследовательности
и
.
Обе имеют бесконечное число членов,
т.к. если бы хоть одна из них состояла
бы из конечного числа, это означало бы,
что члены ряда
не меняют знака, начиная в какого-то
номера. Т.е. отбросив конечное число
членов ряда
, мы получим знакопостоянный ряд,
сходимость которого эквивалентна
абсолютной сходимости, а по условию
теоремы ряд сходится условно.
Т.о.
можно рассмотреть два знакоположительных
ряда
и
.
Оба они расходятся. Докажем это.
Рассмотрим частичные суммы
,
,
,
Последовательность
- расходится, а
- сходится. Последние три последовательности
состоят из положительных членов.
Пусть среди первых N членов ряда k положительных и m отрицательных, тогда
Т.к.
,
то хотя бы одно из слагаемых
или
так же стремится к бесконечности. Т.к.
- сходится, то обе
и
так же стремится к бесконечности, иначе
бы их разность не могла бы стремиться
к конечному числу.
Итак,
оба ряда
и
расходятся.
Тем ни менее члены обоих этих рядов
стремятся к нулю, т.к. являются членами
сходящегося ряда
.
Т.е.
и
.
Из
членов условно сходящегося ряда
составим ряд по следующему алгоритму:
Будем
брать слагаемые из
до тех пор, пока частичная сумма ряда
не превзойдет A. Частичные суммы ряда
бесконечно возрастает, поэтому рано
или поздно они превысят выбранное нами
A. Сразу в этот момент остановимся.
Разность между частичной суммой и A при
этом не превышает последнего слагаемого.
Далее
будем брать слагаемые из
до тех пор пока частичная сумма нашего
ряда на станет меньше чем A. Это опять
же рано или поздно произойдет, т.к.
- расходится и следовательно его частичные
суммы сколь угодно велики. Остановимся
в тот самый момент когда сумма нашего
ряда станет меньше, чем A. Разность между
частичной суммой и A при этом не превышает
последнего слагаемого.
Продолжая
действовать подобным образом, мы получим
ряд, составленный из членов исходного
ряда, взятых в другом порядке. При этом
частичные суммы этого ряда стремятся
к A (их разность не превышает
).
Т.о. наш ряд сходится к A.
Мораль.
От перемены мест слагаемых в бесконечная сумма не меняется, только если соответствующий ряд сходится абсолютно!!!
§13. Признаки Дирихле и Абеля для рядов с произвольными комплексными членами.
Докажем некоторые достаточные признаки сходимости рядов.
Предварительно рассмотрим одно преобразование сумм
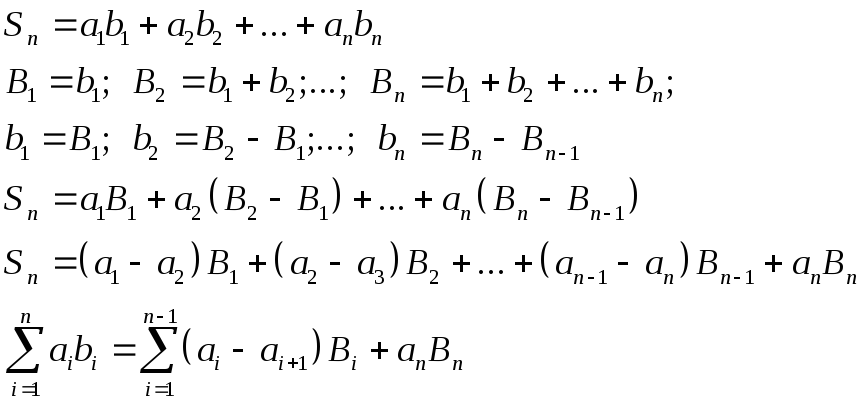
Такое преобразование частичных сумм называется преобразованием Абеля. С его помощью докажем неравенство Абеля.
Лемма (неравенство
Абеля). Если
и
,
то
.
Доказательство.
Т.к.
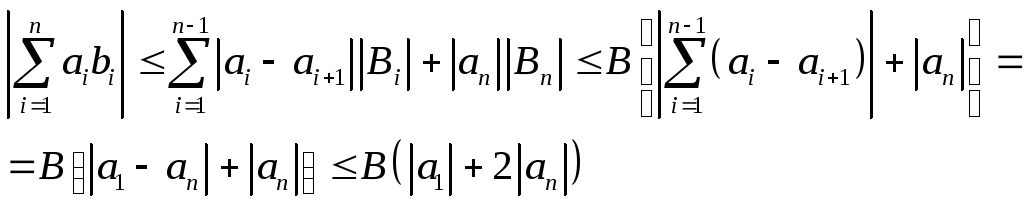
Важно, что оценка дается модулем первого и последнего члена и не зависит от числа слагаемых.
Замечание.
Доказательство проходит и в случае
.
Т.е. можно потребовать просто монотонности
.
Признак
Дирихле.
Пусть дан ряд
:
последовательность {an}
– монотонно стремится к 0, а последовательность
частичных сумм{Bn}
ряда
- ограничена, тогда ряд
- сходится.
Доказательство.
N():
n>
N()
Теперь применяем неравенство Абеля
.
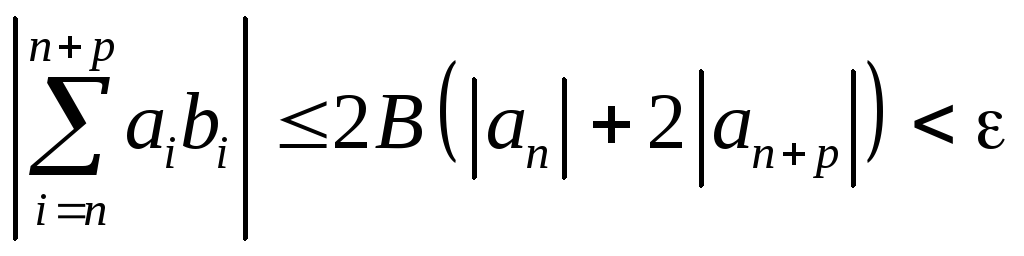Согласно
критерию Коши ряд
сходится.
__________________
Докажем,
что частичные суммы
и
ограничены при
(при
первая сумма равна 0, а вторая не
ограничена).
Действительно
Сумма
первых n
членов
геометрической последовательности с
первым членом
и знаменателем
есть
Действительная
и мнимая части этого выражения не
превосходят
.
Примеры.
-
.
Последовательность {1/n}
– монотонно стремится к нулю. А
последовательность
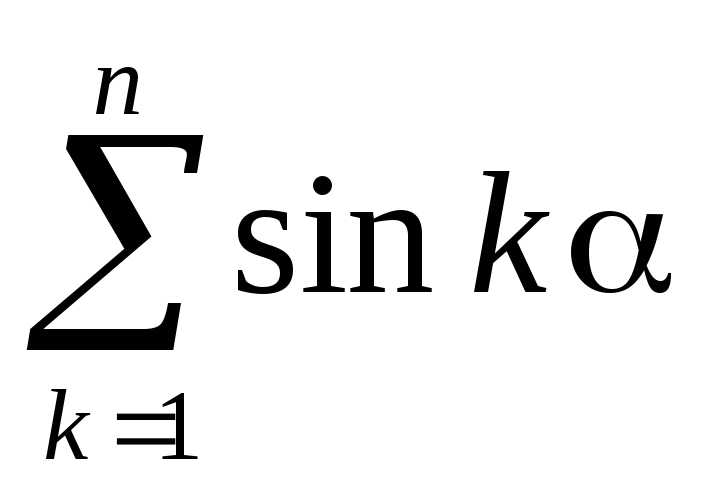- ограничена
по признаку Дирихле исходный ряд
сходится. -
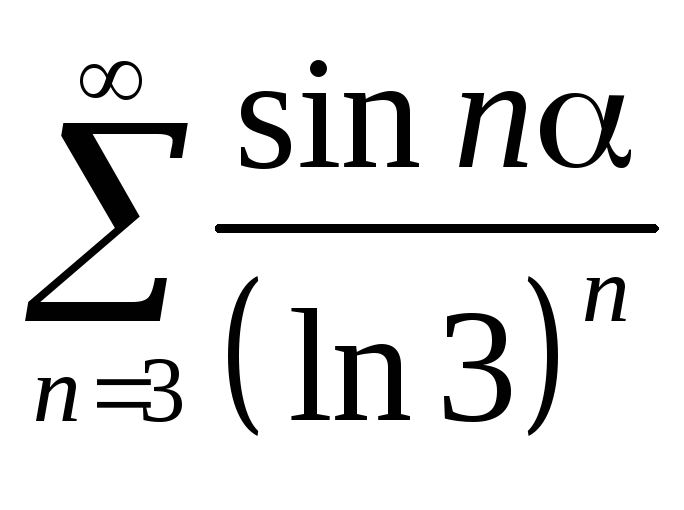3.
Признак
Абеля. Если
последовательность {an}
монотонна и ограничена, а ряд
сходится, то ряд из произведений
также сходится.
Доказательство.
М:
Выберем
произвольное .
Из сходимости
N():
n>
N()p>0
.
Тогда согласно неравенству Абеля
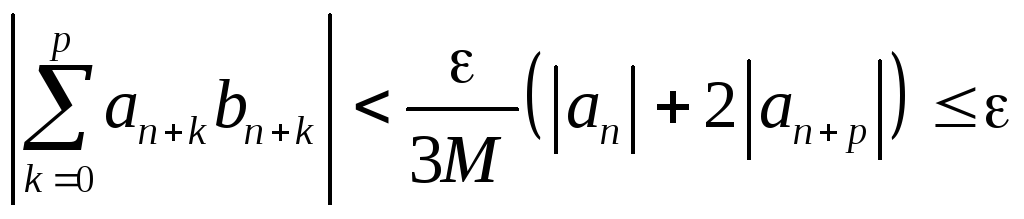
Согласно
критерию Коши ряд
сходится.
____________________________________________
Пример.
Ряд
сходится по признаку Дирихле. А
последовательность
ограничена и монотонна
по признаку Абеля исходный ряд сходится.