§3. Непрерывность функции комплексной переменной. 1. Понятие предела (предельного значения) функции комплексной переменной в точке z₀g.

Определение 1. (по Гейне) Комплексное число w₀ называется пределом f(z) в точке z₀g, если для  {z_n}z₀ соответствующая последовательность {f(z_n)}  w₀.

Определение 2. (по Коши) Комплексное число w₀ называется пределом f(z) в точке z₀g, если для  >0  (,z₀)>0 : |f(z)-w₀|< , как только 0<| z-z₀|<.

f(z)= w₀.

Теорема 3.1. Определения по Гейне и по Коши эквивалентны.

Доказательство. 1) (КошиГейне). Пусть f(z) удовлетворяет О2. Возьмем  >0 и выберем соответствующее ()>0. Рассмотрим произвольную последовательность {z_n} z₀ и найдем N[ ()]=N(): для  n>N() 0<|z_n-z₀|< . Тогда по условию O2 0<|f(z_n)-w₀|< для  n>N(). А т.к. >0- любое и {z_n}z₀-произвольная, то это значит, что {f(z_n)}w₀, т.е. выполнено O1.

2) (ГейнеКоши). Предположим противное: пусть верно O1, а O2- неверно.

Это значит, что ₀>0, что _n>0  z_ng, что 0<|z_n-z₀ |<_n , будет выполнено |f(z)-w₀|>₀. Выберем {_n}0 и соответствующую ей последовательность {z_n}, удовлетворяющую предыдущим неравенствам. Тогда получим, что  {z_n}z₀, а {f(z_n)}не сходится к w₀. Т.е. О1 неверно. Получили противоречие. 

2. Непрерывность функции.

Определение. Функция комплексной переменной f(z), z g, называется непрерывной в точке z₀ g, если  ограниченный предел f(z)= w₀ и w₀= f(z₀).

Определение. (в терминах - Функция комплексной переменной f(z), z g, называется непрерывной в точке z₀ g, если   >0  (,z₀)>0 :  z : |z-z₀|< ; |f(z)-f(z₀)| <.

Определение. Функция комплексной переменной f(z), z g, называется непрерывной в области g, если она непрерывна в  z g.

f(z) C(g).

f(z)=u(x,y)+iv(x,y)

Теорема 3.2. Необходимым и достаточным условием непрерывности f(z) в g (f(z) C(g)) является требование, чтобы u(x,y) и v(x,y) были непрерывны в области g плоскости (x,y) по совокупности переменных.

Справедливость теоремы следует из определения непрерывности функции двух переменных по совокупности переменных.

§4. Дифференцирование функции комплексной переменной. Понятие аналитической функции комплексной переменной.

1. Дифференцирование функций комплексной переменной. Понятие аналитической функции.

Пусть f(z) C(g).

Определение. f(z) называется дифференцируемой в точке z₀g, если при z0 (z=z-z₀) конечный предел разностного отношения .

.

Теорема 4.1. Если f(z)=u(x,y)+iv(x,y) дифференцируема в точке z₀, то u_x(x₀,y₀), u_y(x₀,y₀), v_x(x₀,y₀), v_y(x₀,y₀), причем они связаны условиями Коши-Римана: u_x(x₀,y₀)=v_y(x₀,y₀) ; u_y(x₀,y₀)=-v_x(x₀,y₀).

Доказательство. z=x+iy.

1. z=x0

=u_x(x₀,y₀)+iv_x(x₀,y₀).

2. z=iy0

=-iu_y(x₀,y₀)+v_y(x₀,y₀).

 u_x(x₀,y₀)=v_y(x₀,y₀); u_y(x₀,y₀)=-v_x(x₀,y₀) 

Пусть f(z)C(g) и f(z)=u(x,y)+iv(x,y).

Теорема 4.2 Если в точке z₀=(x₀,y₀)g первые дифференциалы функций u(x,y) и v(x,y) и первые частные производные этих функций в точке (x₀,y₀) связаны условиями Коши-Римана, то f(z) - дифференцируемая функция в точке z₀.

Доказательство. u= u_x(x₀,y₀)x+u_y(x₀,y₀)y+(x,y),

(x,y)=o(|z|)

v= v_x(x₀,y₀)x+v_y(x₀,y₀)y+(x,y),

(x,y)=o(|z|).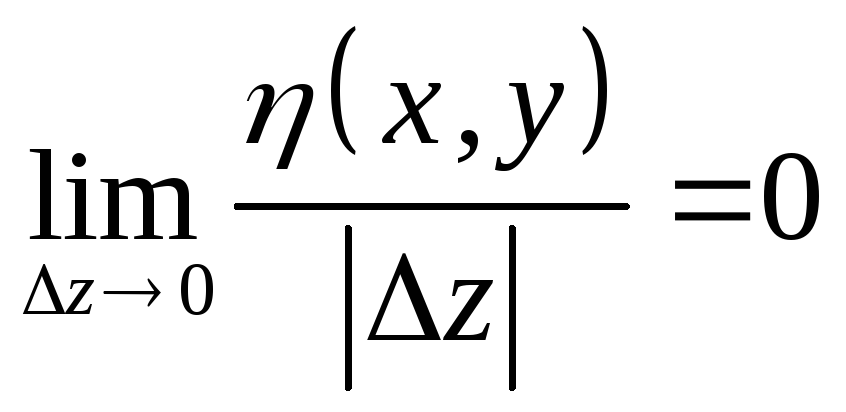

(x,y)=(x,y)+i(x,y).

=(т.к. u_y=-v_x и v_y=u_x)=

=

=u_x(x₀,y₀)+iv_x(x₀,y₀)+

=> 

Замечания. 1) Эквивалентные формы записи производной:

f'’(z)=u_x(x,y)+iv_x(x,y)=v_y(x,y)+iv_x(x,y)=u_x(x,y)-iu_y(x,y)=v_y(x,y)-iu_y(x,y)

2) Равенство равносильно тому, что для >0 ()>0: ||<как только |z|<. => Если f(z) дифференцируема в точке z₀, то она и непрерывна в этой точке. Обратное, вообще говоря, неверно.

2. Определение функции f(z) аналитической в области. Необходимое и достаточное условие аналитичности f(z).

Определение. Функция f(z) называется аналитической функцией в области g, если она дифференцируемая во всех точках zg и ее производная непрерывна в этой области f ' (z) C(g)

f(z) C ^ (g).

Теорема 4.3. Необходимым и достаточным условиями аналитичности функции f(z)=u(x,y)+iv(x,y) в области g, являются непрерывность первых частных производных u_x, u_y, v_x, v_y и связь их условиями Коши-Римана.

Доказательство. Необходимость.

f(z)C^(g) => (z) C(g) => u_x, u_y, v_x, v_y C(g). Выполнение условий Коши-Римана следует из Теоремы 4.1.

Достаточность.

u_x, u_y, v_x , v_y  C(g) => первые дифференциалы функций u(x,y), v(x,y) => по Теореме 4.2  f '(z) =u_x+iv_x C(g); непрерывность следует из непрерывности u_x , v_x.

Замечание. В дальнейшем будет показано, что

f(z)C^ (g) => (z)C^ (g) и для n  f⁽ⁿ⁾(z)C^(g).

3. Свойства аналитической функции комплексной переменной.

1) Действительная и мнимая части аналитической функции – гармонические функции (удовлетворяют уравнению Лапласа):

u_xx+u_yy=u=0 ; v_xx+v_yyv=0

Доказательство: и => и => u_xx+u_yy=0 ;

2) f(z)=u(,)+iv(,) условия Коши-Римана в полярных координатах z=e^i :

v_ = u_ , u_ =- v_.

Доказательство. Замена переменных

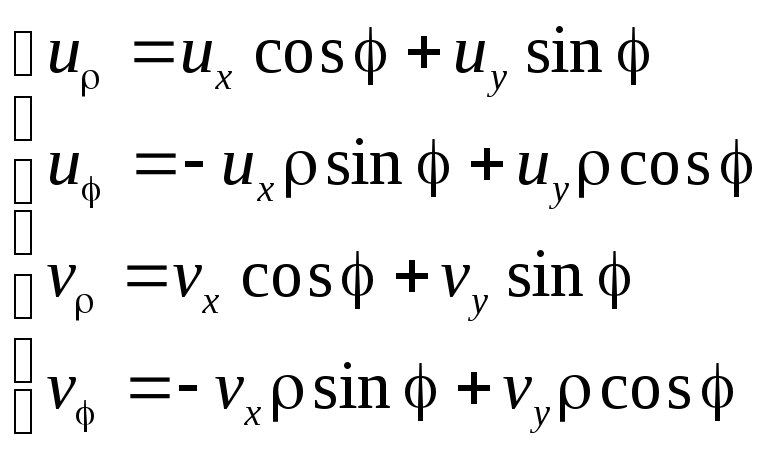
Используя условия К-Р в декартовых координатах, имеем

Выражаем частные производные в декартовых координатах

Запишем выражение для производной в полярных координатах

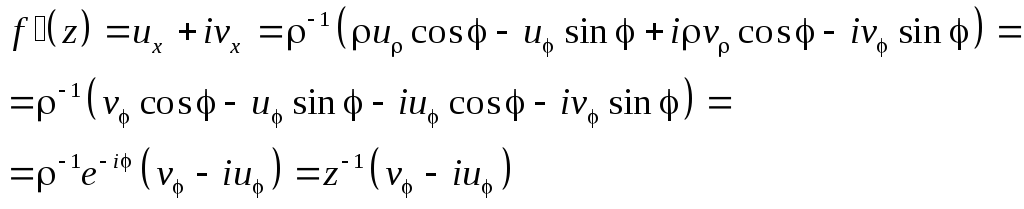
3) f(z)=R(x,y)e^i(x,y) :

R_x=R_y, R_y=-R_x

4) Сумма и произведение аналитических функций есть аналитическая функция. Частное аналитических функций есть аналитическая функция всюду, где знаменатель отличен от нуля.

5) Если w=f(z)C^(g) и (область ее значений G) и

= (w)C^(G), то сложная функция F(z)=[f(z)]C^(g) -аналитическая функция комплексной переменной z в области g.

6) Пусть w=f(z)=u(x,y)+iv(x,y)C^(g) и f '(z₀)0, z₀g. Тогда в окрестности точки w₀=f(z₀) определена обратная аналитическая функция z=(w)C^(|w-w₀|<), отображающая эту окрестность на окрестность точки z₀, причем '(w₀)=1/.

Доказательство. u=u(x,y), v=v(x,y)

=u_xv_y-u_yv_x=u_x²+v_x²=|f'(z₀) ²|0.

(якобиан преобразования отличен от нуля).

z=(w); .

7) Пусть в односвязной области g плоскости (x,y) задана гармоническая функция u(x,y) и известно, что она является действительной частью аналитической функции f(z). Тогда мнимая часть этой функции определяется с точностью до аддитивной постоянной.

Доказательство. По известной функции u(x,y) определяем ее частные производные. Из условий Коши-Римана получим дифференциальные уравнения для мнимой части, из которых она находится с точностью до аддитивной постоянной. 

Аналогично по известной мнимой части можно определить реальную часть аналитической функции.

8) Линии уровня действительной и мнимой части аналитической функции ортогональны в любой точке.

Доказательство. Ортогональность кривых линий  ортогональность их нормалей. Нормаль к линии уровня – градиент функции.

grad u=(u_x,u_y), grad v=(v_x,v_y),

Составим скалярное произведение (grad u, grad v)=u_xv_x+ u_yv_y=- u_y v_y+ u_y v_y=0.

4