Лекции / семестр3 / Альшина (МП-2) / Pr3

§5. Интеграл от функции комплексной переменной по кривой на комплексной плоскости. 1. Вспомогательные положения.

1. Кусочно-гладкая кривая-

{z: z=z(t)=x(t)+iy(t), где t [a,b]}

x(t), y(t)  C[a,b]; x'(t), y'(t) -кусочно- непрерывные на [a,b]; x'²(t)+y'²(t) 0 - нет точек возврата, нет самопересечений.

Если x(a)=x(b), y(a)=y(b), то кривая замкнута.

z₀, z₁,…, z_n – точки разбиения кривой C

z_i=z_i-z_i-1

- частичная сумма

- произвольная точка i-ой дуги.

Определение. Если при существует предел частичных сумм, не зависящий ни от способа разбиения кривой C, ни от выбора точек , то этот предел называется и интегралом от функции комплексной переменной f(z)=u(x,y)+iv(x,y) по кривой C

.

f(z) z = [u(x,y)+iv(x,y)] (x+iy)= ux-vy +i [ vx+uy]

.

Действительная и мнимая части есть интегральные суммы криволинейных действительных интегралов второго рода

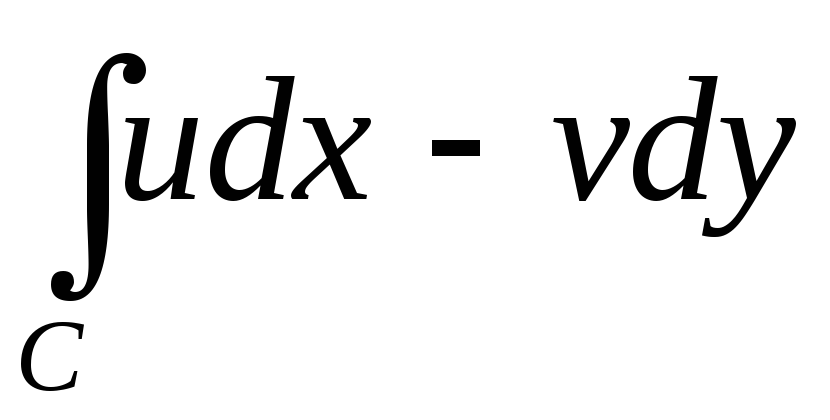и .

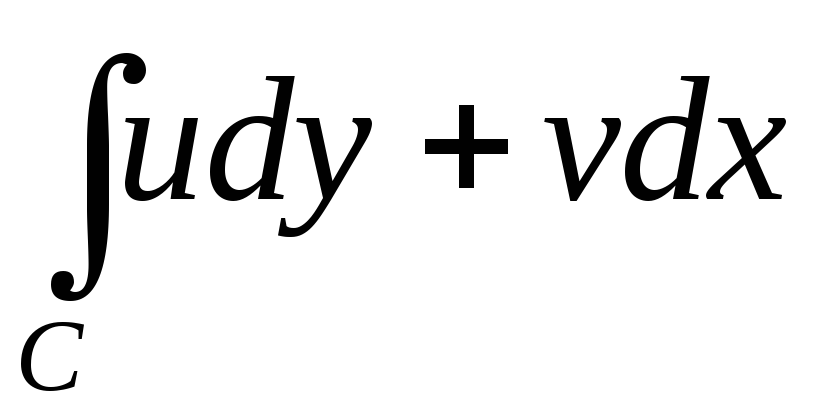Замечания. 1) Достаточное условие существования криволинейных интегралов второго рода, а тем самым и интеграла по комплексной переменной, является кусочная непрерывность и ограниченность |f(z)|. => Интеграл по комплексной переменной существует и для неаналитической функции.

2) 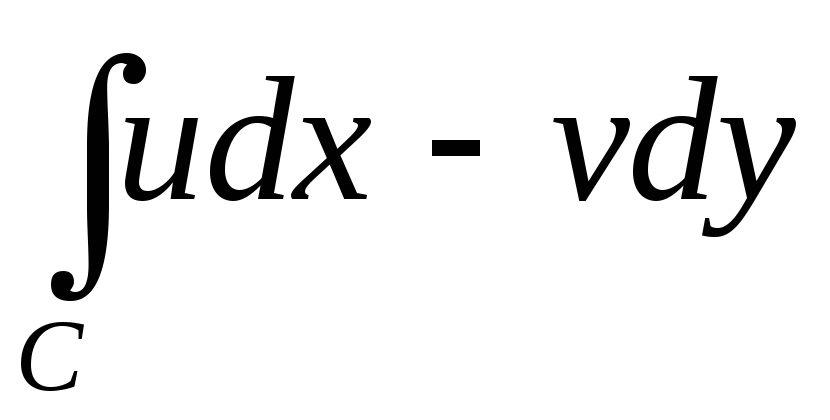+i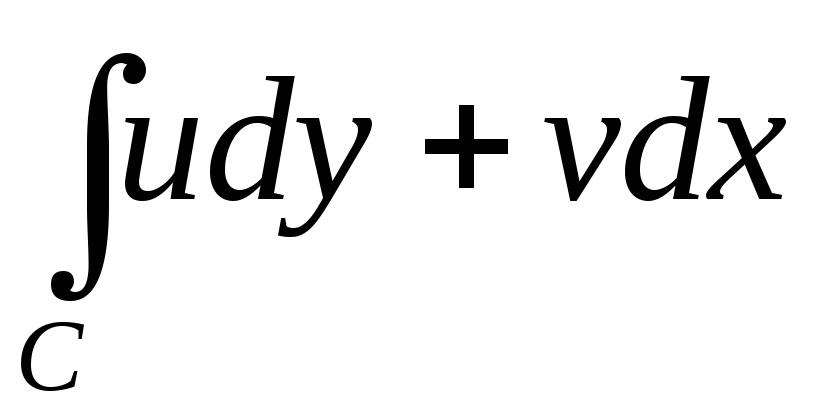. Это соотношение иногда принимают за определение интеграла по комплексной переменной.

2. Свойства .

=-.

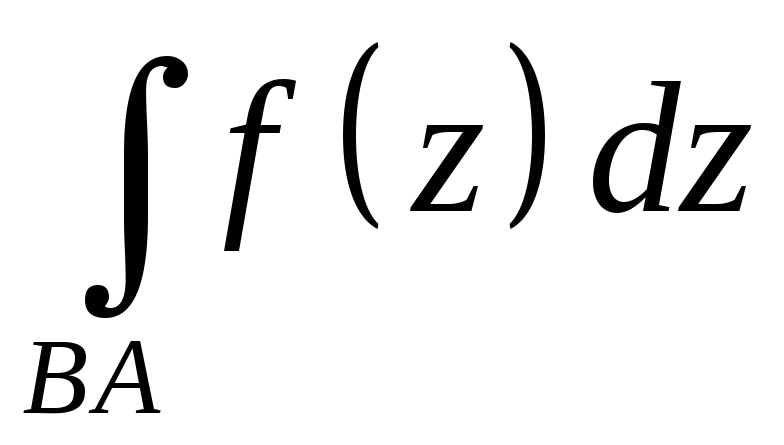2) +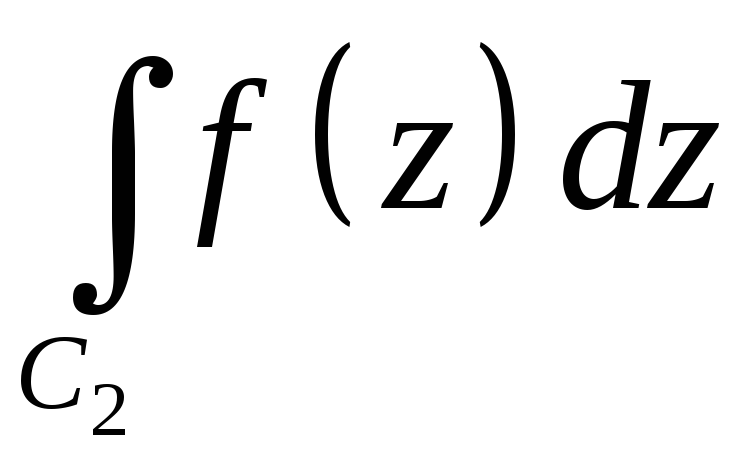= - аддитивность.

3) Линейность

=+.

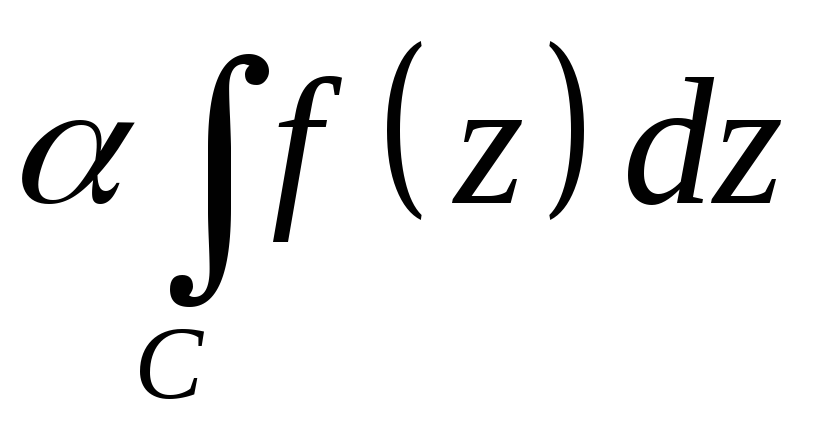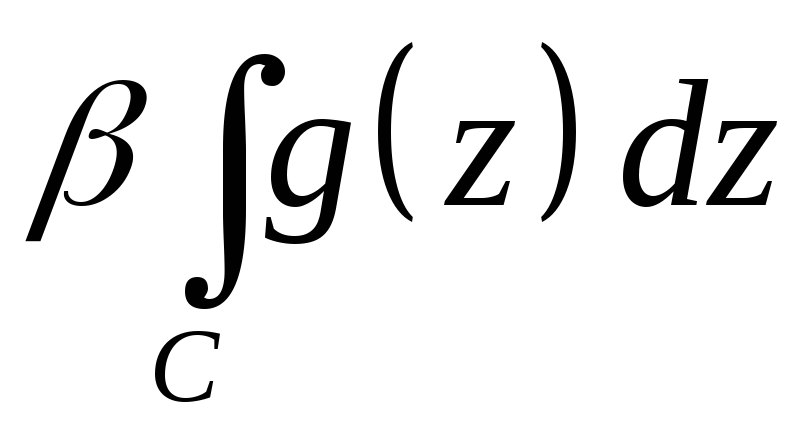4) 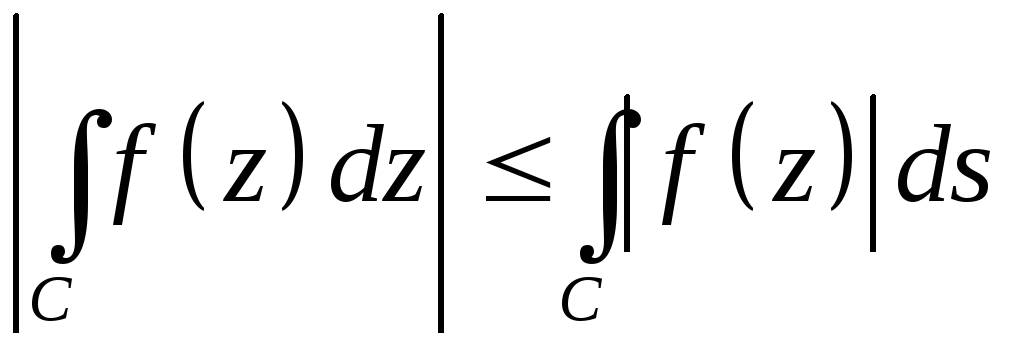(неравенство треугольника)

Если и L - длина кривой C, то .

5) Имеет место формула замены переменной

,

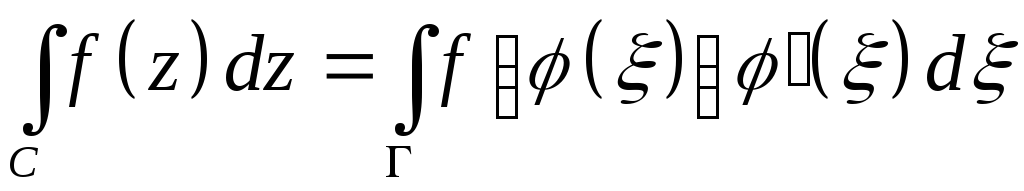здесь - аналитическая функция, устанавливающая взаимнооднозначное соответствие между кривыми C и .

Пример. ,

,

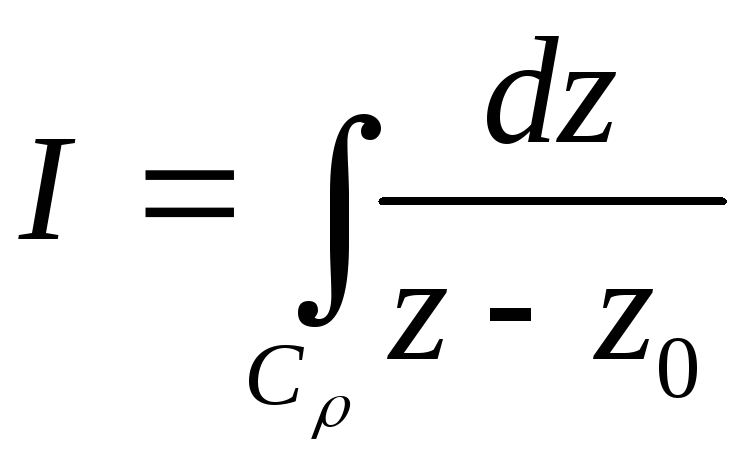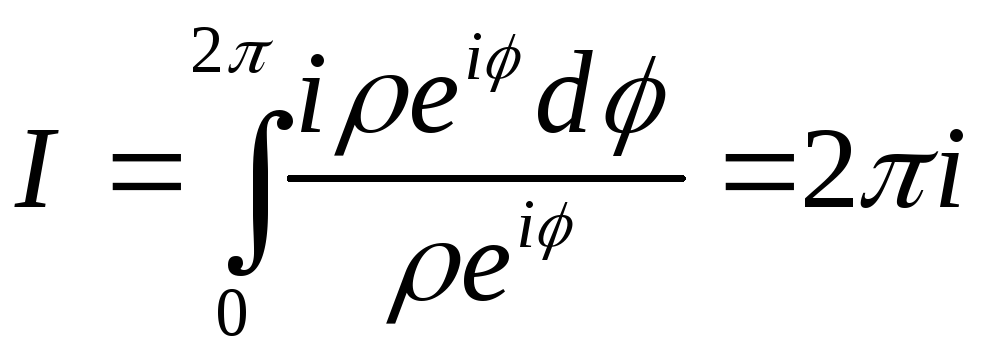- результат не зависит ни от , ни от z₀ !!!

3. Направление обхода замкнутого контура.

Поскольку значение интеграла по замкнутому контуру зависит от направления интегрирования, условимся в качестве положительного направления обхода контура принимать направление, при котором внутренняя область, ограниченная данным замкнутым контуром, остается слева от направления движения. Интегрирование в положительном направлении будем обозначать символом 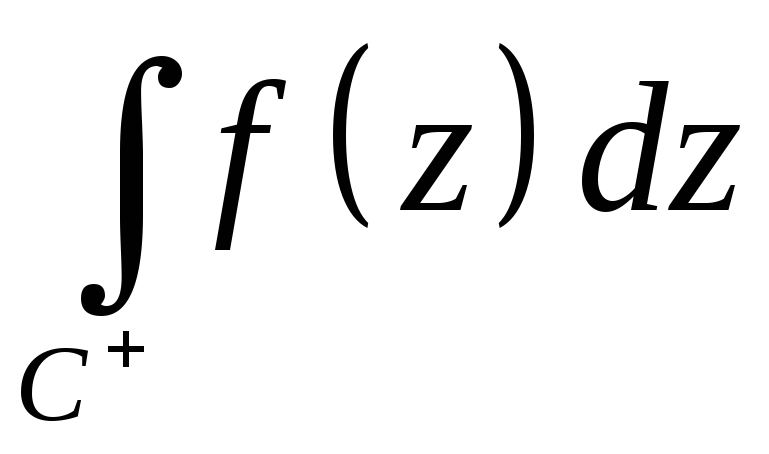или просто , интегрирование в отрицательном направлении - символом .

§ 6. Теорема Коши.

1. Вспомогательные положения.

Формула Грина. Пусть P(x,y), Q(x,y) C(), g – кусочно-гладкий контур и P_x, P_y, Q_x, Q_y C(g), тогда

.

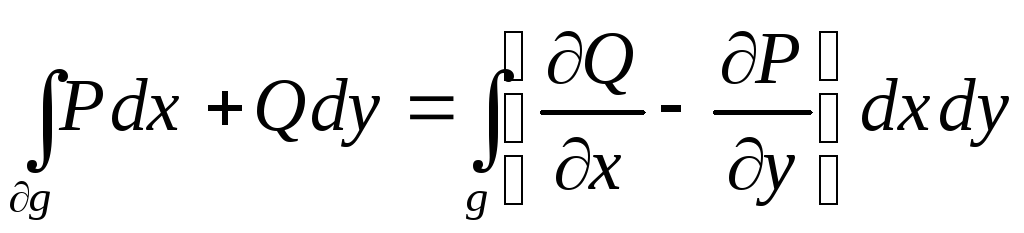2. Теорема Коши. Случай многосвязной области.

Определение. Область называется односвязной, если  две точки ее границы можно соединить непрерывной кривой, полностью принадлежащей границе области. В противном случае область называется многосвязной.

Теорема Коши. Если f(z)C^(g), в односвязной области g, то для замкнутого контура C g

.

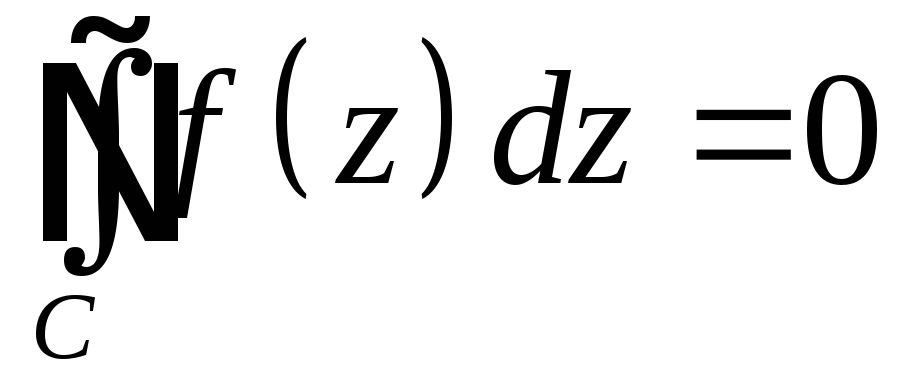Доказательство.

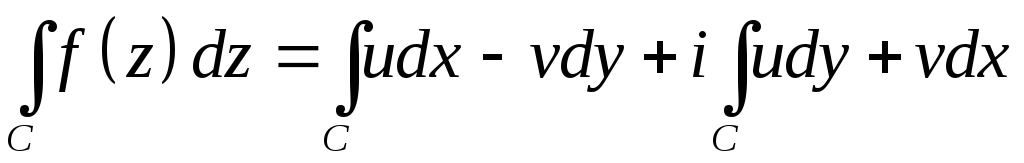=(формула Грина)=

= (-v_x-u_y)dxdy+i(u_x-v_y)dxdy=(условия Коши-Римана)=

= (u_y-u_y)dxdy+i(v_y-v_y)dxdy=0. 

Замечание. 1) Требование односвязности области является существенным!

g = {z: 1<|z|<3} f(z)=1/zC^(g).

.

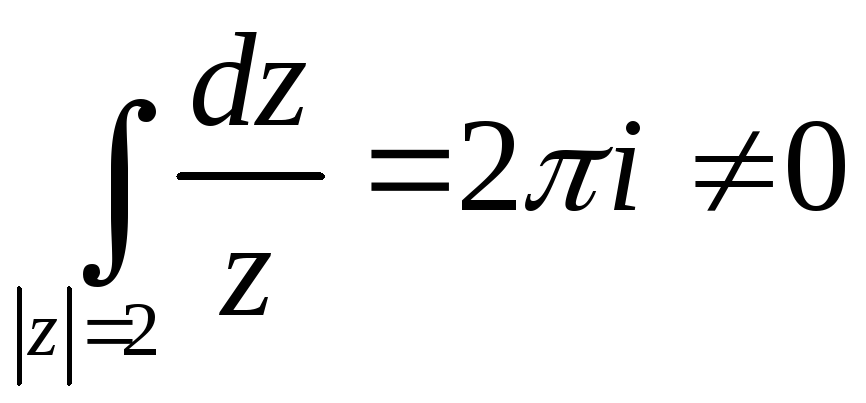Определение Функция называется аналитической в замкнутой области f(z)C^(), если f(z)C^(g). и f(z)C().

Теорема Коши (вторая формулировка). Если f(z)C^(), g-односвязная, то .

Теорема Коши для многосвязной области. Пусть f(z)C^(), g-многосвязная, ограниченная извне контуром C₀, а изнутри контурами C₁, C₂,...,C_n . Тогда .

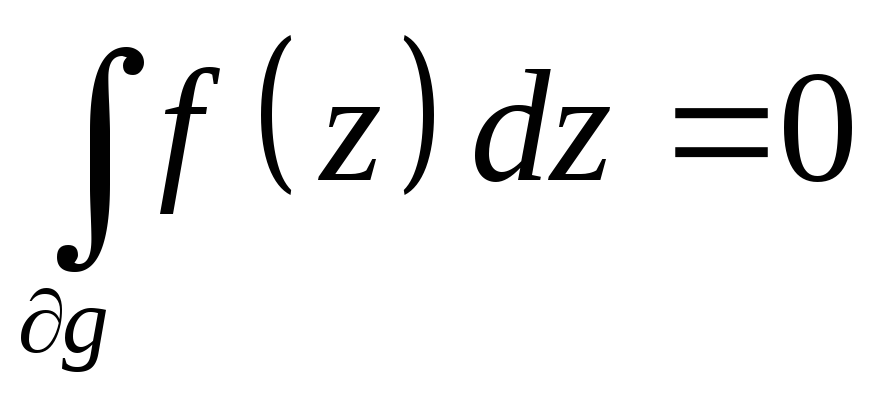g= C₀C₁C₂...C_n

Доказательство. Проведем гладкие кривые 1,2,...,n, соединяющие контур C0 с контурами C1, C2,...,Cn и не пересекающиеся между собой. Тогда область, ограниченная кривыми C0,C1,C2,...,Cn и кривыми 1,2,...,n, проходимыми дважды в противоположных направлениях

окажется односвязной => интеграл по границе этой области равен 0. Но интегралы по вспомогательным кривым ₁,₂,...,_n проходятся дважды в противоположных направлениях и при суммировании интегралов выпадают.

• . 

3. Неопределенный интеграл функции комплексной переменной.

Если g- односвязная и f(z)C^(g), то для z₁, z₂g не зависит от пути интегрирования Т.о. при фиксированном z₀ интеграл - функция только z!

Определение. Пусть g-односвязная область, f(z)C(g) (не обязательно аналитическая!) и для  замкнутого контура g 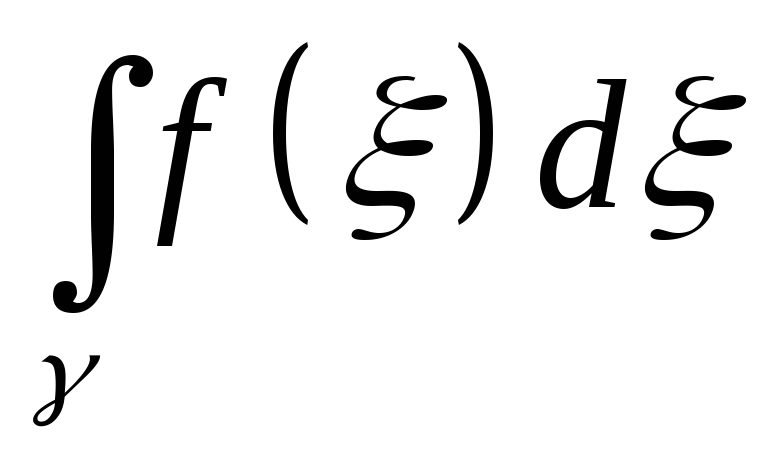=0. Функция - называется неопределенным интегралом от f(z).

Теорема 6.1.

Пусть g-односвязная, f(z)C(g) и для  замкнутого контура g 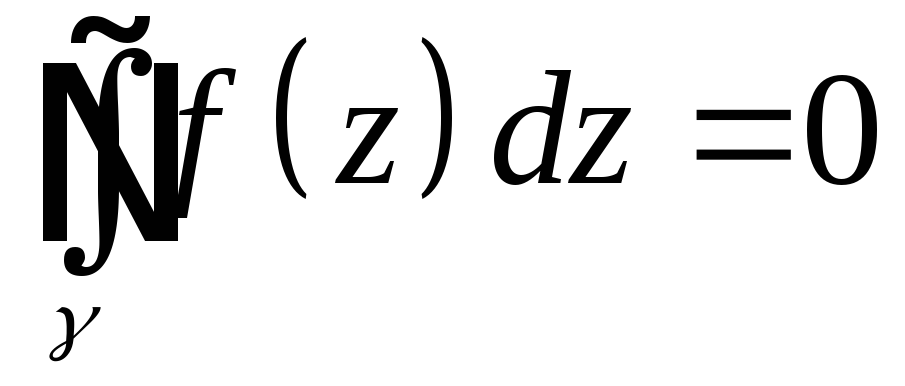, тогда 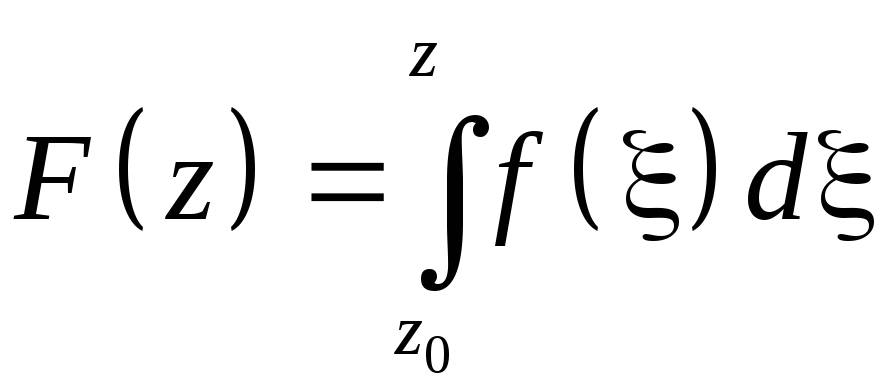, F(z)C^(g) и .

Доказательство.

В силу 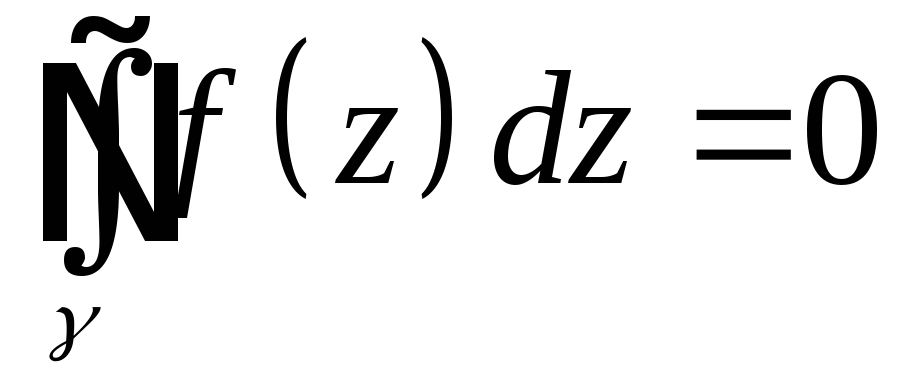для  замкнутого контура не зависит от пути интегрирования => можем взять отрезок прямой, соединяющий точки z и z

В силу непрерывности f(z) правая часть неравенства может быть сделана меньше <0 для =>

.

Т.о. F(z) – неопределенный интеграл от функции комплексного переменного f(z).

И F(z) – аналитическая, т.к. ее производная по условию теоремы непрерывна.

4