Лекции / семестр3 / Алфимов / Course_09

Лекция 8

14. Функциональные ряды.

14.1 Понятие функционального ряда.

Пусть fuk(z)g - последовательность функций (вообще говоря, от комплексного аргумента z 2 G, ãäå G - некоторое множество в комплексной плоскости). Выражение

X1

uk(z)

k=1

называется функциональным рядом, заданным в G. При каждом конкретном z имеем числовой ряд, сходящийся или расходящийся.

Определение: Если при любом z 2 G соответствующий числовой ряд сходится к некоторому комплексному числу f(z), òî f(z) называется суммой функционального ряда, а сам ряд называется сходящимся в G.

Если ряд сходится в G то для любого z 2 G:

Этот ряд определен во всей комплексной плоскости. Все члены ряда действительны, причем ряд знакочередующийся. Он сходится по признаку Лейбница и остаток ряда не превосходит своего первого члена

Таким образом, ряд сходится при любом z.

1

14.2 Равномерная сходимость функционального ряда.

P1

Определение: Ряд k=1 uk(z) называется равномерно сходящимся в G, åñëè

Замечание: Понятие равномерной сходимости бессмысленно без указания множества, где эта равномерная сходимость рассматривается. Один и тот же ряд может равномерно сходиться в одной области и неравномерно сходиться в другой.

Пример: (геометрическая прогрессия) Рассмотрим ряд

f(x) = X1 xk

k=1

Используя формулу суммы бесêîíечно убывающей геометрической прогрессии, заключаем, что f(x) = 1¡1x ïðè ¡1 < x < 1. Хвост ряда равен

Построим графики Rn(x) при различных n как функций x. Заметим что:

Рис. 1: Графики R2(x), R3(x),R4(x), R5(x).

2

²Âñå Rn(x) стремятся к бесконечности при x ! 1;

²Ïðè x ! ¡1 Rn(x) ! 1=2 ïðè n нечетных, в то время как Rn(x) !

¡1=2 ïðè n четных;

²При каждом фиксированном x, x 6= 1 è x 6= ¡1 limn!1 Rn(x) = 0

Âкаждой точке интервала (¡1; 1) остатки Rn(x) стремятся к нулю с ростом n. Поэтому при каждом значении x 2 (¡1; 1) ряд сходится. В то же время

равномерной сходимости на интервале x 2 (¡1; 1) нет. Наличие равномерной сходимости на x 2 (¡1; 1) означало бы, что для любого " > 0 нашелся

бы такой номер N("), ÷òî äëÿ âñåõ n > N(") все графики Rn(x) лежали бы в полоске (¡"; ") (см. рис.1). Это, очевидно не так. В то же время, можно

показать, что равномерная сходимость1 имеет место на любом интервале

x 2 (¡1 + ±; 1 ¡ ±), ± > 0.

Теорема 14.1 (Критерий Коши равномерной сходимости ряда) Если 8" > 0 9N(") такое, что для всех n > N(") è m > 0 и для любых z 2 G имеет место

венство jf(z)¡Sn(z)j < "=2. Ïðè m > 0 имеем также jf(z)¡Sn+m(z)j < "=2. Следовательно

" "

jSn+m(z) ¡ Sn(z)j < j(f(z) ¡ Sn(z)) ¡ (f(z) ¡ Sn+m(z))j < 2 + 2 = "

что и требовалось доказать.

Достаточность. Зафиксируем любое z 2 G. При этом конкретном z имеем

числовой ряд, для него выполняется критерий Коши, следовательно, он сходится. Таким образом, в G определена функция f(z) = limn!1 Sn(z).

Далее, возьмем некоторое "; по условию 9N("), такое, что при 8n > N(") è

m > 0 имеет место неравенство jSn+m(z)¡Sn(z)j < "=2. Тогда при n > N(") имеем

jf(z) ¡ Sn(z)j · jf(z) ¡ Sn+m(z)j + jSn+m(z) ¡ Sn(z)j

1Действительно, при любом n хвост ряда можно оценить сверху через значения на концах интервала (¡1 + ±; 1 ¡ ±)

При любом ± > 0 Rn0 стремится к нулю с ростом n. Таким образом 8" > 0 можно найти такой номер N("), ÷òî ïðè âñåõ n > N(") è äëÿ âñåõ x 2 (¡1+±; 1¡±) будет выполняться

неравенство

jRn(x)j · Rn0 < "

что и означает равномерную сходимость.

3

Для каждого фиксированного z теперь выберем m, таким большим, чтобы

"

jf(z) ¡ Sn+m(z)j < 2

(это можно сделать т.к. f(z) = limn!1 Sn(z)). Тогда при n > N

"

jf(z) ¡ Sn(z)j < 2 + jSn+m(z) ¡ Sn(z)j < "

что и требовалось доказать.

Найдем наибольшее и наименьшее значение n-го члена на всей числовой прямой. Для этого возьмем производную

2Карл Вейерштрасс (1815-1897) - немецкий математик

4

Таким образом, на всей числовой прямой модуль n-го члена рассматри-

ваемого функционального ряда мажорируется членом сходящегося ряда, значит ряд сходится равномерно на всей числовой прямой.

Доказательство: Напомним, что означает непрерывность f(z) в точке z1: 8" > 0 9±, такое, что при jz2 ¡ z1j < ± имеем jf(z2) ¡ f(z1)j < ".

Òàê êàê uk(z) 2 C(G) òî ïðè ýòîì æå n > N(") существует такое ± > 0, ÷òî ïðè jz1 ¡ z2j < ± имеем

Знаменатель меньше единицы при всех действительных x, за исключением x = 0. Поэтому при x =6 0 сумма ряда равна

1 ¡x2 1 = 1 + x2

1+x2

5

Вместе с тем при x = 0 все члены ряда равны нулю. Таким образом

Сумма ряда разрывна в нуле, следовательно, на любом интервале числовой прямой включающем точку x = 0 равномерной сходимости нет.

2. Найдем limx!+0 f(x) åñëè

X1 e¡n2x

f(x) =

n=0 2n + x

Ïðè x < 0 данный ряд расходится так как не выполнено необходимое усло-

вие. При любом x ¸ 0 ряд сходится. На отрезке x 2 [0; 1], включающем нуль, справедлива оценка

ZX1 Z

k=1

выполняется неравенство

jRn(z)j < L ãäå

Xn

Rn(z) = f(z) ¡ uk(z);

k=1

3Вообще говоря, не требуется, чтобы G была областью. Например, G может совпадать с самим контуром (что нами будет использовано в дальнейшем).

6

(здесь, как обычно, ds - элемент длины). Теорема доказана.

причем ряд в правой части последнего равенства сходится равномерно в G.

Доказательство: Так как область конечна и односвязна, можно указать такую конечную длину L, что любые две точки можно соединить кусочно

гладкой кривой4 длины меньше L. Аналогично предыдущей теореме, из

Примеры:

1. Рассмотрим бесконечно убывающую геометрическую прогрессию при

jxj < 1, x 2 R.

Как уже было показано, ряд в правой части равномерно сходится на любом интервале x 2 (¡1 + ±; 1 ¡ ±), ± > 0. Следовательно, при t 2 (¡1 + ±; 1 ¡ ±)

справедливо равенство

2. Рассмотрим другую бесконечно убывающую геометрическую прогрессию при jxj < 1, x 2 R

4Интуитивно - понятно, но вообще это утверждение также нужно доказывать. Примем без доказательства.

7

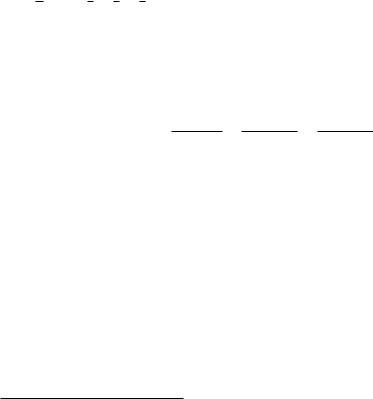
Ряд в правой части равномерно сходится на любом интервале x 2 (¡1 +

±; 1 ¡±), ± > 0. Следовательно, при t 2 (¡1 + ±; 1 ¡±) справедливо равенство

Отсюда - один шаг до того, чтобы посчитать сумму ряда Лейбница

¼4 = 1 ¡ 13 + 15 ¡ 17 + : : :

подставив в полученный ряд t = 1. Но мы пока не можем сделать этот шаг, так как геометрическая прогрессия не сходится при x = 1 т.е. равномерной сходимости на всем отрезке [¡1; 1] нет (хотя формула верна5). Зато мы можем получить другой интересный ряд для числа ¼, подставив в полученный

Теорема 14.6 (теорема Вейерштрасса) Пусть все члены ряда uk(z) - аналитические функции в G è ðÿä

X1

k=1

P 5Справедливость этой формулы гарантируется еще одной Теоремой Абеля: Если ряд 1 an сходится, то

n=1

Док-во см. напр. в книге Б.М.Макаров, М.Г.Голузина, А.А.Лодкин, А.Н.Подкорытов, Избранные задачи по вещественному анализу, СПб, Невский Диалект, 2004

8

(3) ряд из производных сходится равномерно в G

Доказательство:

1. Если все члены ряда (1) - аналитические (а, следовательно, и непрерывные) функции, то согласно Теореме 14.3, сумма ряда f(z) также непре-

рывна в G. Если - любой замкнутый контур, целиком лежащий в G, то по Теореме 14.4

ZX1 Z

k=1

Тогда по теореме Мореры f(z) аналитична в G. Кроме того, любой остаток ряда Rn(z) = f(z) ¡ Pn uk(z) - также аналитическая в G функция (как

k=1

разность аналитических функций).

2. Рассмотрим произвольную точку z0 2 G и контур ½, представляющий собой окружность с центром в z0 и радиусом ½ достаточно малым, таким, чтобы весь контур целиком поместился в G. Очевидно, что так как

X1

f(z) = uk(z)

k=1

òî

причем сходимость последнего ряда равномерная6 на контуре ½. Таким образом, обе части последнего равенства можно проинтегрировать в положительном направлении по контуру ½

из чего по формуле Коши получаем

X1

f(p)(z0) = u(kp)(z0) k=1

Íî z0 - любая точка области, следовательно п.2 доказан.

9

3. Докажем равномерную сходимость ряда (2). Для этого необходимо оценить остаток ряда

Снова возьмем произвольную z0 2 G и контур ½, рассмотренный в п.2. Так êàê Rn(z) аналитическая функция, то по формуле Коши имеем

Далее, ряд (1) сходится равномерно, следовательно 8" > 0 9N(") единое для всей области G такое, что

"½p jRn(z0)j < p!

Но тогда

Тем самым п. 3 также доказан.

Для рядов с действительными членами верна следующая теорема Теорема 14.7. Пусть

² функции uk(x) непрерывно дифференцируемы на отрезке [a; b]

² ряд, составленный из производных P1 u0k(x) равномерно сходится

k=1

íà [a; b]

² ðÿä P1 uk(x) сходится хотя бы в одной точке c 2 [a; b]

k=1

P1

Тогда ряд k=1 uk(x)

(1) равномерно сходится на всем отрезке [a; b],

(2) его сумма s(x) непрерывно дифференцируема,

(3) s0(x) = P1 u0k(x).

k=1

10