Лекции / семестр3 / Алфимов / Course_10

Лекция 10

15. Степенные ряды.

15.1 Определение степенного ряда. Область сходимости степенного ряда.

Определение: Степенным рядом называется функциональный ряд вида

X1

cn(z ¡ z0)n

n=1

Здесь z0 è cn, n = 1; 2; : : : - комплексные числа. Числа cn, n = 1; 2; : : :

называются коэффициентами ряда.

Изучим область сходимости степенного ряда. Теорема 15.1 (Теорема Абеля). Если степенной ряд

n=1

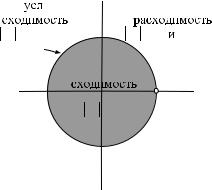
сходится в точке z1, то он сходится и в любой точке, расположенной ближе к z0, ÷åì z1, причем в любом замкнутом круге Gk = fjz ¡ z0j · kjz1 ¡ z0jg, ïðè k 2 (0; 1), сходимость ряда равномерная.

z1

z

Gk z0

Рис. 1: К доказательству теоремы Абеля.

Доказательство: Пусть z - произвольная точка круга Gk. Представим n-é ÷ëåí ðÿäà â âèäå

cn(z ¡ z0)n = cn(z1 ¡ z0)n ¢ µ z ¡ z0 ¶n z1 ¡ z0

1

Заметим, что так как ряд (1) сходится в точке z1, то в силу необходимого условия сходимости ряда существует M такое, что jcn(z1 ¡ z0)nj · M ïðè

âñåõ n. Получаем следующую оценку

Таким образом, в круге Gk, k 2 (0; 1) сходимость ряда во-первых, абсолютная (так ряд из модулей мажорируется бесконечно убывающей геометри- ческой прогрессией и, следовательно, сходится), а во-вторых, равномерная (по признаку Вейерштрасса, Теорема 14.2). Теорема доказана.

Следствия :

1.Если степенной ряд (1) расходится в точке z2 6= z0, то он расходится в любой точке, отстоящей от z0 дальше, чем z2. Действительно, если бы ряд сходился в какой-нибудь точке z3, отстоящей от z0 дальше, чем z2, òî ïî теореме Абеля он сходился бы и в z2.

2.Область сходимости степенного ряда - круг (говоря это, все же будем иметь в виду, что этот круг может иметь как нулевой, так и бесконечный радиус, вырождаясь, соответственно, в точку или во всю комплексную плоскость). Радиус этого круга называется радиусом сходимости степенного ряда. Вне круга ряд расходится, а на границе круга - может и сходиться и расходится (например, в некоторых точках сходиться, в некоторых - расходиться).

Верхний предел последовательности определен всегда, хотя может быть бесконечным. Используя признак Коши, заключаем, что область сходимости ряда определяется равенством

1 jz ¡ z0j < l

то есть ряд сходится в круге, радиуса R = 1=l. Формула

называется формулой Коши-Адамара1. Åñëè l = 0, ряд сходится во всей комплексной плоскости (R = 1), åñëè l = 1, ряд сходится только в точке z = z0 и больше нигде (R = 0).

1Жак Адамар (1865-1963) - французский математик

2

3. Пусть ряд (1) сходится в круге jz¡z0j < R. Тогда его сумма - аналити- ческая функция. Действительно, все члены ряда - аналитические функции, а по теореме Абеля ряд сходится равномерно в любом замкнутом круге jz ¡ z0j · ½, ½ < R. Следовательно, в любом таком круге сумма ряда является аналитической функцией по Теореме Вейерштрасса (Теорема 14.6). Значит, она аналитическая во всем открытом круге jz ¡ z0j < R.

4. Пусть область сходимости ряда (1) - открытый круг радиуса R, jz ¡

z0j < R, и сумма ряда равна функции f(z). Тогда при jz ¡ z0j < R справедливы формулы

Действительно, по теореме Абеля наш ряд сходится равномерно в любом замкнутом круге G½ = fjz ¡ z0j · ½g, 0 < ½ < R и его (ряд) в этом круге можно дифференцировать (по Теореме 14.6) и интегрировать (по Теореме 14.5). Так как 0 < ½ < R - произвольно, то формулы (2) и (3) будут спра-

ведливы во всем открытом круге jz ¡ z0j < R. При этом полученные ряды (стоящие в правой части формул (2) и (3)) будут снова сходиться равномерно в G½ при любом 0 < ½ < R, следовательно, дифференцирование и интегрирование можно повторять сколько угодно раз.

то заключаем, что радиус сходимости не меняется при дифференцировании или интегрировании степенного ряда.

Пример: Рассмотрим ряд

X1 zn

n=1 n

Используя формулу Коши-Адамара, найдем его радиус сходимости

r

Следовательно, ряд сходится в круге jzj < 1 и расходится вне его. Изучим

сходимость ряда на границе, jzj = 1. Абсолютной сходимости на границе, очевидно, не будет, так как ряд из модулей совпадает с гармоническим

3

рядом, и, соответственно расходится. Запараметризуем границу, введя действительный параметр '; тогда на границе имеем z = ei'. Подставим по-

следнее выражение в ряд

' =6 2¼k, k 2 Z первый ряд сходится по признаку Дирихле. При ' = 2¼k, k 2 Z он расходится, это соответствует точке z = 1. Второй ряд сходится по признаку Дирихле при любом '. Значит, исходный ряд сходится на границе условно всюду, кроме одной точки z = 1 (ñì. Ðèñ.2).

.

1

z <1

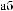
15.2 Разложение в ряд аналитических функций.

Рассмотрим теперь другую задачу: каким образом можно сопоставить данной аналитической функции f(z) степенной ряд, который бы сходился

ê f(z) в некотором круге? Ответ на этот вопрос дает Теорема Тейлора:

Теорема 15.2 (Теорема Тейлора). Если f(z) - аналитическая функция в круге jz ¡ z0j < R, то существует единственный степенной ряд

4

Доказательство: Возьмем любую внутреннюю точку круга z, jz ¡ z0j < R. Построим какую-нибудь окружность C½ с центром в точке z0 и радиусом ½ < R, так, чтобы z лежала внутри нее. Функция f(z) аналитична внутри

причем последний ряд сходится равномерно внутри окружности C½. Значит, этот ряд можно подставить в формулу Коши и проинтегрировать

что и доказывает существование и единственность разложения.

Замечание: Представление функции f(z) рядом (4)-(5) называется разло-

жением функции в ряд Тейлора. Разложение в ряд Тейлора, очевидно, имеет те же формулы для коэффициентов, что и в формуле Тейлора, которая изучалась на первом курсе. Можно сказать, что разложение в ряд Тейлора соответствует разложению по формуле Тейлора из 1-го курса анализа при наличии аналитичности функции - т.е. очень сильном дополнительном условии, которое на первом курсе не изучалось.

Таким образом, вспоминая формулу Тейлора, можно записать разложения в ряды для основных элементарных функций

5

1. Экспонента:

ez = X1 zn

n=0 n!

(напомним, что эта формула следует непосредственно из того, что (ez)(k) = ez). Экспонента - функция аналитическая во всей комплексной плоскости,

поэтому разложение справедливо во всей комплексной плоскости. Можно проверить по формуле Коши-Адамара, что радиус круга сходимости равен бесконечности:

(мы воспользовались формулой Стирлинга). 2. Синус и косинус

Для вывода можно использовать,например, явные формулы для производных

Синус и косинус - функции, аналитические во всей комплексной плоскости, соответственно представления их рядами также справедливы во всей комплексной плоскости2.

3. Геометрическая прогрессия

Ряд абсолютно сходится внутри круга jzj < 1 (проверяется формулой Коши-

Адамара), вне этого круга расходится. На границе круга ряд также расходится, так как n-й член ряда не стремится к нулю.

4. Главная ветвь логарифма

ln(1 + z) = ¡ X1 (¡1)n zn n

n=1

2Утверждается, что именно из сравнения рядов для синуса, косинуса и экспоненты Эйлер вывел свою знаменитую формулу ei' = cos '+i sin ' (проверьте формулу Эйлера,

подставив в нее эти три ряда!)

6

Этот ряд получается интегрированием ряда для геометрической прогрессии (см. параграф 14, где аналогичный ряд был получен для действительных значений переменной). Ряд абсолютно сходится внутри круга jzj < 1 àáñî-

лютно, на границе круга ряд сходится условно всюду, кроме точки z = ¡1 (проверьте, запараметризовав границу формулой z = ei' и используя пред- ставление (¡1)n = ein¼).

5. Главная ветвь арктангенса

arctg z =

X1 (¡1)nz2n+1

2n + 1

n=0

Этот ряд можно (см. параграф 14) получить интегрированием ряда для геометрической прогрессии

Геометрическая прогрессия равномерно сходится в круге jzj < 1, следова-

тельно, ряд для арктангенса также равномерно (и абсолютно) сходится в этом круге. Можно проверить (опять же, запараметризовав границу круга z = ei' и используя признак Дирихле), что во всех точках границы, кроме

z = i è z = ¡i этот ряд сходится условно. В точках z = i è z = ¡i этот ряд расходится.

6. Степенная функция с произвольным действительным показателем. При любом действительном ® имеем

dk (1 + z)® = ®(® ¡ 1) : : : (® ¡ k + 1)(1 + z)®¡k dzk

Поэтому получаем ряд3

(1 + z)® = 1 + X1 ®(® ¡ 1) : : : (® ¡ n + 1)zn n!

n=1

При натуральных ® ряд обрывается после конечного числа членов (при

этом получается формула бинома Ньютона). При прочих действительных ® ряд абсолютно сходится при jzj < 1 (проверьте, здесь удобно применить

признак Даламбера) и расходится при jzj > 1. На границе круга сходимости4 ряд сходится абсолютно при ® > 0, расходится при ® · ¡1 è

сходится условно во всех точках границы кроме z = ¡1 ïðè ¡1 < ® < 0.

3Разложение справедливо также при ® комплексном при надлежащем выборе ветви многозначной функции w = (1 + z)®.

4Примем без доказательства.

7