§13. Задачи на построение в аксонометрической проекции.

След-е зад мы будем использовать при построении сечений многогранников.

Зад 1. Прямая (a, a₃) лежит в плоск. заданной тремя точками (A, A₃), (B, B₃), (C, C₃), не лежащими на одной прямой. По заданной прямой a построить a₃.

Реш.Строим прямые AB, A₃B₃, AC, A₃C₃, BC, B₃C₃. Мы договорились, что направление проецирования не параллельно рассматриваемым прямым и плоскостям. Поэтому точки A, B, C не лежат на одной прямой

и прямые AB, AC, BC не совпадают. Прямая a пересекает две из этих прямых в точках M и N. По этим точкам мы можем построить вторичные проекции M₃ и N₃ (для этого необходимо провести прямые параллельные OE₃). Тогда a₃=M₃N₃.

И наоборот, если задана прямая a₃, мы можем найти M₃ и N₃, по ним найти M и N. Тогда a=MN. Но здесь возможна ситуация, когда A₃, B₃, C₃ лежат на одной прямой. Тогда задача не имеет решения.

Зад 2.Точка (X, X₃) лежит в плоскости заданной тремя точками (A, A₃), (B, B₃), (C, C₃), не лежащими на одной прям. По заданной точке X₃ построить X.

Реш.Точка (X, X₃) лежит в одной плоскости с точками (A, A₃), (B, B₃), (C, C₃). Поэтому прямые (XC, X₃C₃) и (AB, A₃B₃) лежат в одной плоскости. Пусть они пересекаются в точке (M, M₃) (если эти прямые не

пересекаются, то пересекаются прямые (XA, X₃A₃) и (BC, B₃C₃), и мы рассмотрим их). Строим:1. M₃=X₃C₃A₃B₃;

2. m||OE₃, M₃m; 3. ABm=M;

4. l||OE₃, X₃l; 5. lCD=X.

Аналогично по точке X можем найти X₃.

Задача 4. Плоскость задана тремя точками (A, A₃), (B, B₃), (C, C₃), не лежащими на одной прямой. Построить её след.

Решение. Прямые (AB, A₃B₃) и (AC, A₃C₃) лежат на плоскости  их следы лежат на следе плоскости. Строим:

1. X=ABA₃B₃, Y=ACA₃C₃;

2. p=XY – след.

Если какая-либо из прямых не имеет следа, то вместо неё рассмотрим прямую (BC, B₃C₃

§14. Полные и неполные изображения.

Пусть  – плоскость изображений. Говорим, что точка M; ¯ задана, если задана её аксонометрическая проекция и одна из вторичных проекций, например, M₃. Прямая a считается заданной, если заданы 2её точки или её аксонометрическая и вторичная проекции. Плоскость считается заданной, если заданы элементы, которые её однозначно определяют (например, три точки, которые не принадлежат одной прямой, прямая и точка или две прямые).

Пусть на плоск. дано изображение F некоторой фигуры F; ¯. Это изобр-ие наз. полным, если к нему можно присоединить изобр-ие R аффинного репера так, что все прямые, точки и плоск, которые определяют фигуру F, будут заданы.

Пр1. Данное изображение параллелепипеда является полным. Если к нему присоединить изображение R ={A, B, D, A₁} аффинного репера, то все вершины будут заданы, т.е. у каждой вершины можно указать аксонометрическую и вторичную проекции. Напр, у вершины A; ¯ – (A, A), у B₁ – (B₁, B).

Оказывается свойство изображения быть полным или неполным не зависит от выбора присоединённого репера (без д-ва). Если в последнем примере выбрать за изображение репераR ={A, B, D, D₁}, то вторичная проекция точки B₁ будет отсутствовать, но её можно построить. Для этого нам нужно провести через B₁ прямую параллельную AD₁ до пересечения с прямой BC

П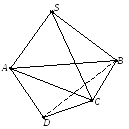р2 изображение шестигранника не явл. полным. Если к нему присоединить изображение R ={A, B, C, S} аффин.репера, то вершины A; ¯, B; ¯, C; ¯, S; ¯ будут заданы, а D; ¯ – нет. У неё есть аксонометрическая проекция D, а в качестве вторичной проекции можем взять любую точку D₃, принадлежащую прям.l||AS, проходящей через D, даже если эта точка будет находиться за пределами треуг. ABC. На след-ем чертеже мы выбрали точ. K, а точ. L потом однозначно достраивается.

Количество точек, которые необходимо добавить к чертежу, для того, чтобы изображение стало полным, называетсякоэффициентом неполноты изображения. В последнем примере он равен 1.

П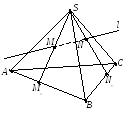р3. Данное изображение тетраэдра и прямой имеет коэффициент неполноты равный 2. Для того чтобы оно стало полным, необходимо добавить точки пересечения прямой с гранями пирамиды (и соответственно, часть линии сделать пунктирной). Мы добавляем точки M и N, а точки M_o и N_o однозначно достраиваются.

Задачи на построение на неполном изображении не имеют единственного решения. Недостающие элементы можно добавлять произвольно.