§18. Построение сечения конуса.

Опять же считаем, что дан след секущей плоскости на плоскости основания и точка на высоте конуса. Точно так же, как и в случае цилиндра, строим два сопряжённых диаметраA_oB_o и C_oD_o основания. При построении используем хорду K_oL_o, один конец которой лежит на контурной образующей. Продлеваем C_oD_o до пересечения со следом и находим

точку X. PX – ось сечения.

Далее строим:

SC_oPX=C, SD_oPX=D.

Отрезок CD изобр-ет большой диаметр сечения.В отличие от цилиндра, малый диаметр

не будет проходить через точку P: он

проходит через середину E отрезка CD. Пусть E_o=SEC_oD_o. Проводим через E_o диаметр основания F_oG_o||A_oB_o, а через точку E проводим прямую l||A_oB_o. Затем, SF_ol=F, SG_ol=G Отрезок FG – изображение малого диаметра сечения.

Далее нам нужно найти точки перехода с видимой стороны на невидимую. Пусть H_o=K_oL_oC_oD_o, H=SH_oCD. Проводим через H прямую h||K_oL_o. Тогда

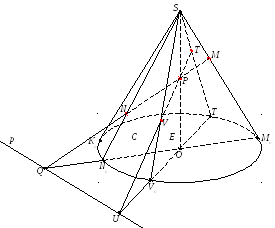K=SK_oh и L=SL_oh – две точки на сечении, в точке K сплошная линия должна переходить в пунктирную. Для того чтобынайти вторую такую точку M, надо аналогичным образом воспользоваться хордой M_oN_o. Для того, чтобы не загромождать изображение, мы покажем только результат.

Далее мы покажем другой способ, как можно найти любое количество точек на сечении. Пусть  – эллипс, изображающий основание. Мы выбираем любую точку V_o. Проводим диаметр V₃T₃ и продолжаем его до пересечения со следом.

Получим точку U. Построим диаметр V_oT_o, SV_oUP=V, ST_oUP=T.

Точки V и T принадлежат сечению. В частности, среди всех точек на  следует выбрать точки, лежащие на контурных образующих. Тогда мы найдём точки K и M, в

которых сплошная линия на сечении перех-т в пунктирную. На чертеже показано построение точки M.

§19. Построение сечения шара.

Рас-им только сечения шара параллельные или перпендикулярные экватору.

Зад1. Дано очертание сферы g и изображение её экватора – эллипс g_o. Построить сечение сферы плоскостью параллельной экватору и делящей радиус сферы пополам.

Решение.Из условия задачи следует, что сечением сферы будет окружность, центр O1;¯ которой делит отрезок O; ¯N; ¯ или O; ¯S; ¯ пополам. Построим сначала изображение полюсов.Пусть AB – это большой диаметр эллипса g_o, изображающего экватор, CD – малый. Проведём касательную к эллипсу g_o в точке С. Пусть K – точка её пересечения с очертанием сферы. Тогда ON=OS=CK. Откладываем эти отрезки на прямой CD от точки O и получаем изображение полюсов. Затем находим середины O₁ и O₂ отрезков ON = OS.

Для того чтобы найти длину отрезка A₂B₂, изображающего большой диаметр сечения, мы воспользуемся вспомогательным чертежом. На нём мы изобразим «оригинал» меридиана, проходящего через точки A; ¯, N; ¯, B; ¯, S; ¯ тем же радиусом, что и очертание сферы. Построим середины O1;¯ и O2;¯ отрезков O; ¯N; ¯ и O; ¯S; ¯, проведём через них хорды A1;¯B1;¯ и A2;¯B2;¯параллельные A; ¯B; ¯. Тогда на изображении большие диаметры сечений A₁B₁ и A₂B₂ будут иметь такую же длину.

Заметим, что их концы ни в коем случае не будут лежать на очертании сферы.

Эллипсы ₁ и ₂, изображающие сечения, будут подобны изображению экватора. Поэтому B₂С₂||BС. Это позволяет найти вершину С₂, а

затем иD₂. Мы имеем два главных диаметра эллипса ₂ и можем применить любой из способов построения дополнительных точек на эллипсе, для того чтобы изобразить эллипс ₂. Для того чтобы не загромождать чертёж, мы на первом чертеже изобразили только сечение ₂. Этот эллипс касается очертания сферы(точки L и M),и в этих точках видимая часть линии переходит в неви­димую. Изобразим теперь сферу вместе с двумя сечениями без вспомогательных линий, использовавшихся при построении.