41 Принцип взаимности поляр.

Теорема 5.6.1. Если точка B принадлежит поляре точки A, то A принадлежит поляре точки B.

Пусть кривая  имеет уравнение (5.1.1), а точки A и B – координаты a_i и b_i . Пусть p(A) и p(B) – поляры точек A и B. Ур-ие p(A):(;\s\do10(i(а_ij a_i) x_j = 0 ; Ур-ие p(B): (;\s\do10(i(а_ij b_i) x_j = 0 ; B p(A)  (;\s\do10(iа_ij a_ib_j = 0  (;\s\do10(iа_ij b_ia_j = 0  A p(B) .

Из этой теоремы вытекает удобный способ построения поляры. Необходимо рассмотреть два случая:

1)из точки A можно провести 2 касат-ые к кривой ;

2) из A нельзя провести ни одной касат-ой к .

1. Пусть l₁ и l₂ – касательные к , проведенные из точки A, а P и Q – точки касания. Тогда l₁= p(P), l₂= p(Q). Значит, A p(P) и A p(Q)  P p(A) и Q p(A)  PQ = p(A).

Тот же рисунок показывает, как построить полюс прямой PQ, если она пересекает .

2. Проведем через точку A две произвольные прямые a и b. Построим полюсы этих прямых: K₁ и K₂. Тогда

A a = p(K₁)  K₁ p(A)

A b = p(K₂)  K₂ p(A)

И обратно, если дана прямая K₁K₂, мы можем построить ее полюс A.

Пример. Дано уравнение кривой : х₁² – х₂² + 2х₃² + 4х₁х₂ – 2х₂х₃ = 0 и точка B(0: 2: –1)  .

Уравнение поляры запишем в матричном виде: B^TAX = 0, или

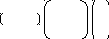
1 2 0 х₁ х₁

0 2 –1 2 –1 –1 х_{2 = 0}; _{ 4 –1 –4} х_{2 = 0}; _

0 –1 2 х₃ х₃

4х₁ – х₂ – 4х₃ = 0

5.7. Полярное соответствие.

Поляра точки A(a_i ), относительно кривой , заданной уравнением (5.1.1), определяется уравнением (5.4.1), которое расписывается в виде (5.3.2 ). Это будет прямая, если не все из следующих чисел равны нулю:

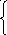u₁= а₁₁ а₁+ а₁₂ a₂+ а₁₃ a_3,

u₂= а₁₂ а₁₊ а₂₂ а₂₊ а₂₃ a_3, (5.7.1)

u₃= а₁₃ а₁₊ а₂₃ а₂₊ а₃₃ a₃

Теорема 5.7.1. Если

а₁₁ а₁₂ а₁₃

= а₁₂ а₂₂ а_{23  0} ,

а₁₃ а₂₃ а₃₃

то каждая точка A(a_i ) имеет, и притом только одну поляру относительно кривой .

Из алгебры известно, что система (5.7.1) при u₁= u₂= u₃= 0 и   0 имеет, и притом, только единственное решение a₁= a₂= a₃= 0. Но проективные координаты точки не могут быть такими. Значит, числа u₁, u₂, u₃ не могут быть все нулевыми, а значит, каждая точка A имеет определенную поляру.

Теорема 5.7.2. Если   0, то каждая прямая имеет, и притом, только один полюс относительно кривой .

Пусть прямая p имеет уравнение u₁x₁+ u₂x₂+ u₃x₃= 0 . Тогда при   0 система (5.7.1) имеет (и притом, только одно) решение a₁, a₂, a₃.

Следствие. Если для кривой  выполняется   0, то она порождает взаимнооднозначное соответствие между множеством всех точек и множеством всех прямых на проективной плоскости.

Это соответствие называется полярным соответствием. В частности, каждая овальная кривая (эллипс, гипербола, парабола) порождает полярное соответствие, т.к. для овальной кривой   0.