1 Аффинныепреобразования.

Опр 1. Преобразование плоскости f:^–  наз. аффинным, если оно действует по формулам вида

(1)

и при этом,  =  0.

В матричном виде формулы (1) можно переписать так:

X= AX + C , (1)

A = , C = .

1. Последовательное выполнение двух аффинных преобр-ний есть аффинное преобр-ние. Преобр-ние обратное к аффинному тоже является аффинным. Тождественное преобр-ние является аффинным. Другими словами, все аффинные преобразования плоскости образуют группу.

2. (Основное св-во аффинных преобр-ний) Аффинное преобр-ние переводит прямые в прям. Параллельные прям. переходят в параллельные.

3. Афф. Преобр-ние однозначно определяется заданием трех точек, не лежащих на одной прямой и их образов: A= f (A), B= f (B), C= f (C).

4. Аффинное преобразование с >0 сохраняет ориентацию плоскости; аффинное преобр-ние с <0 меняет ориентацию плоскости.

5. Аффинное преобр-ие сохраняет простое отношение трёх точек и сохр. пропорциональность отрезков, лежащих на параллельных прямых.

Примем без док-ва, что следующее опр-ние равносильно опр-нию 1.

Опр. 2. Преобразование плоскости называется аффинным, если оно переводит прямые в прямые. Др-и словами, любое преобр-ние плоск-и, переводящее прямые в прямые задаётся формулами (1).

Лемма. Пусть A и B – две точки на прямой l, а f₁ и f₂ – аффинные преобразования плоскости. Если f₁(A)=f₂(A), f₁(B)=f₂(B), то для любой точки M на прямой l выполняется f₁(M)=f₂(M).

Д-во. Пусть A=f₁(A), B=f₁(B). Пусть M – произвольная точка на прямой l и M=f₁(M), M=f₂(M). Пусть =(AB, M). Тогда точки и обе принадлежат прямой l=f₁(l), и обе делят отрезок AB в одинаковом отношении :1. Значит, M=M.

Следствие. Если аффинное преобразование имеет f две неподвижные точки A и B, то и вся прямая неподвижна относительно преобразования f, т.е. f(M)=M MAB.

Теорема 1. Пусть R = {O, A₁, A₂} и R  = {O, A₁, A₂} – произвольные аффинные реперы плоскости . Тогда существует одно и только одно аффинное преобр-ние плоскости, которое переводит репер R в репер R . При этом движении точка M с данными координатами в репере R переходит в точку M с такими же координатами в репере R .

Д-во. Определим отображение f:^–  по следующему правилу. Точке M(x, y)_R сопоставляется точка M(x, y)_R, т.е. имеющая точно такие же координаты, только во втором репере. Мы имеем

O(0, 0)_R , O(0, 0)_R ; A₁(1, 0)_R , A₁(1, 0)_R ; A₂(0, 1)_R , A₂(0, 1)_R .

Поэтому O= f (O), A₁= f (A₁), A₂= f (A₂).

Очевидно, что отображениеf явл. взаимно однозначным. Д-ем, что оно яв-ся аффинным. Пусть l – произв-ая прямая. Тогда относительно репера она задаётся Ур-ем Ax+By+C=0. Но тогда её образ l будет иметь точно такое же Ур-ие, только относ-но репера R . След-но, l тоже явл. прямой.

Д-ем единственность. Предположим, что сущ-ет ещё одно аффинное преобразование g, такое что g(R)=R. Пусть M – произв. точка плоскости. Проведём через M прямую m, которая пересечёт координатные оси OA₁ и OA₂ в точках M₁ и M₂. Согласно лемме

 f(M)=g(M).

Итак, преобразованияg и f одинаково действуют на произвольную точку плоскости. Это значит, что преобразования g и f совпадают.

Следствие. Если аффинное преобразование f имеет три неподвижные точки, которые не лежат на одной прямой, то f – тождественное преобразование.

Поэтому след-ая теор. имеет самост-ное значение.

Теор 2. Любое аффинное преобр-ние плоск-ти переводит репер в репер

Д-во. Пусть f – аффинное преобр-ие, R={O, A₁, A₂} – произв-ый репер, O=f(O), A₁=f(A₁), A₂=f(A₂). Нам требуется д-ть, что R  = {O, A₁, A₂} – тоже репер, т.е. что точки O, A₁, A₂ не лежат на одной прямой. Предп-им прот-ое: эти точки лежат на одной прям. Пусть M – произв-ая точ. плоск, m, M₁ и M₂ – такие же, как в предыдущей теор. (см. чертёж к теор. 1). Точ. M₁OA₁  её образ M₁OA₁; точ. M₂OA₂  её образ M₂OA₂. След-но, прямая m=f(m) совпадает с прямой A₁A₂, а значит, M=f(M)A₁A₂.

Мы показали, что произ-ая точка плоск-и отображается на прямуюA₁A₂, а это значит, что вся плоскость отобр-ся на эту прямую. Поэтому f не явл. преобр-ем. Полученное противоречие показывает, что точки O, A₁, A₂ не могут лежать на одной прямой.

§2. Параллельное проецирование.

Опр. Выберем в пространстве некоторую плоскость  и вектор p;\s\up8(( не параллельный . Пусть A; ¯ – произвольная точка в пространстве. Проведём через A; ¯ прямую, параллельную p;\s\up8((. Эта прям. пересечёт плоск.  в точке A_o, которая наз. параллельной проекцией точки A; ¯ на плоскость  по направлению вектора p;\s\up8((.

Совокупность проекций всех точек фиг. (;¯ сост-ют фигуру_o, которая наз. проекцией фигуры . Если вектор p;\s\up8((, то проекция наз. ортогональной. В дальнейшем рассматриваемые прямые и отрез. не параллел. Вект-у p;\s\up8((.

Свойства параллельного проецирования.

1. Проекция прямой есть прямая.

2.Проекции параллельных прямых параллельны или совпадают.

3. Проекция отрезка A; ¯B; ¯ есть отрезок A_oB_o, где A_o – проекция точки A; ¯, B_o – проекция точки B; ¯.

4.При параллельном проецировании сохраняется простое отношение трёх точек. В частности, проекция середины отрезка A; ¯B; ¯ есть середина отрезка A_oB_o.

5.Проекции парал-ых отрезков, или от­р-ов, лежащих на одной прям, парал-ны или лежат на одной прямой.

6. Проекции параллель­ных отрез, или отр-ов, лежащих на одной прям. пропорц-ны этим отрезкам:

= .

Упр. Д-е их самостоятельно.

Пусть (; ¯ и – две различные плоск, а p;\s\up8(( – вектор не парал-ый этим плоск-ям. Каждой точке M; ¯(; ¯ поставим в соответствие её проекцию M_o на плоск.  параллельно век-у p;\s\up8((. Полученное отобр-ие f:(; ¯ ^–  наз. параллельным проецированием плоскости (; ¯ на плоскость  по направлению век-а p;\s\up8((.

§3. Аффинные отображения.

Опре. Пусть (; ¯ и  – две различные или совпадающие плоскости в пространстве. Взаимнооднозначное отображение f:(; ¯ ^–  наз. аффинным отображением плоскости (; ¯ на плоскость , если любые три точки M1;¯, M2;¯, M3;¯ плоскости (; ¯, лежащие на одной прям, переходят в три точки M₁, M₂, M₃ плоскости , лежащие на одной прямой.

Отобр-ие f:(; ¯ ^–  наз. подобием, если сущ-ет такое чис. k>0, что для любых тчк A; ¯,B; ¯ плоск-и (; ¯ и их образов A_o,B_o в плоск-и  выпол-ся |A_oB_o|=k|A; ¯B; ¯ |.

Если плоскости (; ¯ и  совпадают, то аффинное отображение будет аффинным преобр-ем, а подобие – преобр-ем подобия. Можно д-ть, что аффинное отображение сохраняет простое отношение трёх точек.

Лемма. Подобие является аффинным отображением.

Д-во. Согласно неравенству треугольника |AB|+|BC||AC|, и при этом равенство возможно тогда и только тогда, когда B лежит на отрезке AC.

Пусть f:(; ¯ ^–  – подобие, а M1;¯, M2;¯, M3;¯ – три точки плоск. (; ¯, лежащие на одной прямой. Тогда, если M2;¯ лежит между M1;¯ и M3;¯, то выпол-ся |M1;¯M3;¯|

=|M1;¯M2;¯|+|M2;¯M3;¯|. Пусть M₁, M₂, M₃ – образы этих точек. Тогда

|M₁M₂|+|M₂M₃|=k|M1;¯M2;¯|+k|M2;¯M3;¯|= =k(|M1;¯M2;¯|+|M2;¯M3;¯|)=k|M1;¯M3;¯|=|M₁M₃|.

Аэто означает, чтоM₂ лежит на отрезке M₁M₃.

Примеры аффинных отображений.

1. Параллельное проецирование одной плоскости на другую.

2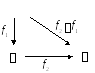. Пусть f₁:(; ¯ ^–  – параллельное проецирование, а f₂:^–  – некоторое аффинное преобразование плоскости  (например, подобие). Тогда отображение f_2f₁:(; ¯ ^–  будет аффинным отображением.

Все свойства аффинных преобразований переносятся и на аффинные отображения. Доказательства следующих теорем получаются из доказательств теорем 1 и 2 заменой слова «преобразование» на слово «отображение».

Теорема 3. Пусть R; ¯ = {O; ¯, A1;¯, A2;¯} и R = {O, A₁, A₂} – произвольные аффинные реперы в плоскостях (; ¯ и  соответственно. Тогда существует одно и только одно аффинное отображение плоскости (; ¯ на плоскость , которое переводит репер R в репер R . При этом движении точка M с данными координатами в репере R переходит в точку M с такими же координатами в репере R .

Теорема 4. Любое аффинное преобразование f:(; ¯ ^–  переводит репер на плоскости (; ¯ в репер на плоскости .

Следствие. Аффинное отображение переводит параллельные прямые в параллельные прямые, луч – в луч, отрезок – в отрезок, полуплоскость – в полуплоскость, угол – в угол.

Аффинная эквивалентность.

Опре. Фигуры  и (;¯, лежащие в плоскостях (; ¯ и  соответственно, наз. аффинно-эквивалентными, если сущ-ет аффинное отображение f:(; ¯ ^– , которое фигуру (;¯ переводит в фигуру . Вершины произвольного треугольника образуют репер. Поэтому из теоремы 3 следует, что произвольные два треугольника A; ¯B; ¯C; ¯(; ¯ и ABC аффинно-эквивалентны.

Теорема 5. Два четырёхугольника, которые лежат в плоскостях (; ¯ и  аффинно-эквивалентны тогда и только тогда, когда их можно обозначить буквами A; ¯B; ¯C; ¯D; ¯ и ABCD так, что для точек E; ¯ = A; ¯C; ¯  B; ¯D; ¯ и E=ACBD будет выполнено

(A; ¯C; ¯, E; ¯)=(AC, E), (B; ¯D; ¯, E; ¯)=(BD, E) (1)

Условие (1) означает, что соответствующие диагонали четырёхугольников делятся точкой пересечения диагоналей в одинаковом отношении.

Д-во. Пусть четырёхугольники аффинно-эквивалентны. Это значит, существует аффинное отображение f:(; ¯ ^– , которое переводит первый четырёхугольник во второй. Обозначим их так, чтобы выполнялось A=f(A; ¯), B=f(B; ¯), C=f(C; ¯), D=f(D; ¯). Тогда отрезок A; ¯C; ¯ переходит в отрезок AC, отрезок B; ¯D; ¯ – в отрезок BD. Точка пересечения отрезков A; ¯C; ¯ и B; ¯D; ¯ переходит в точку пересечения отрезков AC и BD, и при этом сохраняется простое отношение трёх точек. Это означает, что выполняется (1).

Обратно, пусть четырёхугольники обозначены буквами так, что выполнено (1). Рассмотрим аффинное отображение f:(; ¯ ^– , которое переводит репер R; ¯ = {A; ¯, B; ¯, D; ¯} в репер R = {A, B, D}. В силу (1) точка E; ¯ будет переходить именно в точку E. Мы имеем f(A; ¯)=A, f(E; ¯)=E. Значит, луч A; ¯E; ¯ переходит в луч AE, а первое из условий (1) оказывает, что точка C; ¯A; ¯E; ¯ переходит в точку CAE. Таким образом, четырёхугольник A; ¯B; ¯C; ¯D; ¯ переходит в четырёхугольник ABCD.