
Физ.-стат. основы кв. инф.- Богданов (конспект лекций)
.pdf
1.4. Операторы координаты и импульса в координатном и импульсном представлении. Фундаментальные коммутационные соотношения
Свойства х.ф. позволяют ввести оператор координаты в импульсном представлении. Действительно, рассматривая х.ф. как свертку (1.3.2), имеем:
M (x)= −if |
′ |
|
|
|
~* |
∂ ~ |
(p − u)u=0 = |
||
|
|
|
|
|
ψ |
||||
|
|
|
|
|
|||||
(0) = −i∫dpψ (p) |
∂u |
||||||||
|
|
|
∂ |
|
|
|
|
(1) |
|
~* |
(p) |
~ |
(p) |
|
|
|
|||
= i∫dpψ |
|
ψ |
|
|
|
|
|||
∂p |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Таким образом, если в координатном представлении |
|||||||||
координата |
|
описывается |
оператором |
xˆ , сводящимся к |
|||||
умножению |
|
пси- |
функции |
на |
число x , (т.е. |
||||
xˆψ (x) = xψ (x)), |
то |
в импульсном представлении |
|||||||
xˆ = i ∂
оператор координаты есть ∂p .
Аналогичным образом нетрудно показать, что, если в импульсном представлении импульс описывается
оператором |
pˆ , просто |
сводящимся |
к |
умножению |
пси- |
||||
функции на |
число p , |
т.е. |
~ |
|
~ |
|
|||
pˆψ (p) = pψ (p), то в |
|||||||||
координатном представлении |
оператор |
импульса |
есть |
||||||
pˆ = −i |
∂ |
|
|
|
|
|
|
|
|
∂x |
(изменение |
знака |
перед |
мнимой единицей |
|||||
|
|||||||||
i соответствует отличию между прямым и обратным преобразованиями Фурье).
21
Заметим, что операторы координаты и импульса эрмитовы. Переход от координатного представления к импульсному оставляет инвариантным фундаментальное коммутационное соотношение:
pxˆ ˆ − xpˆˆ = −i |
|
|
(2) |
|
|
|
|
В случае нескольких степеней свободы |
|||
представленное каноническое соотношение примет вид: |
|||
pˆ j xˆk − xˆk pˆ j = −iδ jk |
, |
j, k = 1,2,..., s |
(3) |
|
|
||
Здесь s - число степеней свободы
Рассматриваемое соотношение показывает, что каждый импульс не коммутирует только со своей (канонически сопряженной) координатой и коммутирует со всеми остальными координатами.
Все координаты коммутируют между собой, также как и все импульсы коммутируют между собой
xˆ j xˆk − xˆk xˆ j = 0 pˆ j pˆk − pˆk pˆ j = 0
Преобразование, сохраняющее коммутационные соотношения, каноническими.
Преобразование Фурье является частным случаем унитарных преобразований. Оказывается, что в квантовой информатике можно рассматривать произвольные унитарные преобразования. При этом будет происходить замена одного представления на другое, дополнительное по отношению к исходному. Измерения, проводимые в различных представлениях, порождают совокупность
22
взаимнодополнительных распределений. Рассмотренные соображения, изложенные систематическим образом, являются основой постулатов квантовой информатики (см. главу 3).
1.П. Приложение. Дельтафункция и ее свойства.
Мы приведем только краткую сводку некоторых важных свойств дельтафункции. Более полное и строгое изложение вопроса можно найти в [34].
Дельтафункция является важным инструментом в квантовой информатике, поскольку находит широкое применение в теории преобразования Фурье и статистическом анализе взаимнодополнительных распределений.
Проведем исследования выражения (4) из раздела
1.1: |
1 |
|
|
|
|
δ (x − x ) = |
|
exp(ip(x − x ))dp |
|
||
2π ∫ |
(1) |
||||
1 |
1 |
||||
|
|
||||
В точке x1 = x рассматриваемый интеграл заведомо расходится. Проведем его регуляризацию. Ограничим область интегрирования по переменной p в пределах от
− K до |
K . |
Регуляризованная версия |
исходного |
|
соотношения (1) есть: |
|
|||
~ |
1 |
K |
|
|
δ (x − x1 ) = |
|
exp(ip(x − x1 ))dp |
(2) |
|
2π |
||||
|
−∫K |
|
||
Элементарное интегрирование сразу приводит к результату:
23
~ |
|
1 sin(K (x − x1 )) |
|
|
|
||||
δ (x − x1 ) = |
|
|
|
(x − x1 ) |
|
|
(3) |
||
|
π |
|
|
||||||
|
|
|
|
|
|
||||
Заметим, что интеграл от полученной функции |
по |
||||||||
переменной x1 всегда равен единице: |
|
|
|
||||||
+∞ ~ |
|
|
|
|
|
|
|
|
|
∫δ (x − x1 )dx1 = 1 |
|
|
|
(4) |
|||||
−∞ |
|
|
|
|
|
|
|
|
|
Проанализируем |
|
характер |
|
поведения |
|||||
|
|
|
|
|
|
~ |
|
|
|
рассматриваемой |
функции |
δ (x − x1 ). |
Её максимум |
||||||
|
|
|
|
x1 = x и |
~ |
(0) = K / π . |
|
||
находится в |
|
точке |
равен δ |
При |
|||||
больших |
значениях |
обрезающего |
множителя K |
||||||
рассматриваемая функция локализована в интервале
порядка π / K . |
При увеличении K функция становится |
|||||
все более и более локализованной вблизи ноля. |
~ |
(x − x1 ), |
||||
|
|
|
|
|
||
Последовательность |
функций |
δ |
||||
отвечающая |
бесконечно растущей |
последовательности |
||||
значений |
K , |
называется |
дельта- |
образной. |
Дельта- |
|
функцию можно определить как обобщенную сингулярную предельную функцию дельтаобразной последовательности.
Таким образом: |
|
||||
δ (x) = |
1 |
lim sin(Kx) |
(5) |
||
π |
|||||
|
K →∞ |
x |
|
||
Приведем также некоторые другие представления для дельтафункции:
24

δ (x) = |
1 |
lim sin2 (Kx) |
|
|
|
|
|
(6) |
||||
|
π |
|
|
|
|
|
||||||
|
|
K →∞ |
Kx2 |
|
|
|
|
|
||||
δ (x) = lim |
|
1 |
|
|
x |
2 |
|
|
|
|||
|
|
− |
|
2 |
|
(7) |
||||||
2πσ |
exp |
2σ |
|
|||||||||
|
σ →0 |
|
|
|
|
|
||||||
Задача 1.П.1 Обоснуйте представления (6) и (7) для дельтафункции.
Дельтафункция может рассматриваться как производная от ступенчатой функции (функции Хевисайда)
′ |
(8) |
δ (x) = Θ (x), |
где
( ) 1, x ≥ 0
Θ x =
0, x < 0
Основное свойство дельтафункции определяет способ ее интеграции с произвольной несингулярной функцией:
∫δ (x)f (x)dx = f (0) |
(9) |
Нетрудно получить и некоторые другие свойства для дельтафункции
∫δ (x − x0 )f (x)dx = f (x0 ) |
(10) |
||||
∫δ (ax)f (x)dx = |
1 |
|
f (0) |
(11) |
|
|
a |
|
|||
|
|
||||
|
|
|
|
|
|
25
∫δ (g(x))f (x)dx = ∑ |
|
1 |
|
|
f (xi ), |
(12) |
|
|
|
g′(xi ) |
|
|
|||
|
|
||||||
i |
|
|
|
f (x) |
|
||
где xi - простые корни функции |
|
|
|||||
Задача 1.П.2. Обоснуйте приведенные формулы (10)- (12).
26
Глава 2. Точность статистических характеристик гильбертова пространства
Внастоящей главе мы увидим, что различного вида неравенства КошиБуняковского, соотношения неопределенностей, а также неравенства РаоКрамера получаются, посуществу, с помощью одного и того же математического приема, сводящегося к элементарному требованию неотрицательности некоторого квадратного трехчлена. В разделах 2.1- 2.3 с использованием принципов квантовой информатики излагаются элементарные сведения, связанные с неравенством КошиБуняковского и соотношением неопределенностей. В разделе 2.4 представлено так называемое соотношение неопределенностей ШредингераРобертсона. В разделе 2.5 рассмотрено многомерное соотношение неопределенностей. Информация Фишера и неравенство РаоКрамера, известные еще из классической математической статистики, изучаются в разделах 2.6- 2.8 с новой квантовоинформационной точки зрения.
2.1.Неравенство КошиБуняковского для векторов состояния и его статистическая интерпретация
Рассматриваемое неравенство имеет место для произвольных линейных пространств, в которых определено понятие скалярного произведения. Приведем примеры таких пространств.
Вкомплексном конечномерном пространстве C s
размерности s скалярное произведение двух векторов определяется следующей формулой в обозначениях Дирака:
27
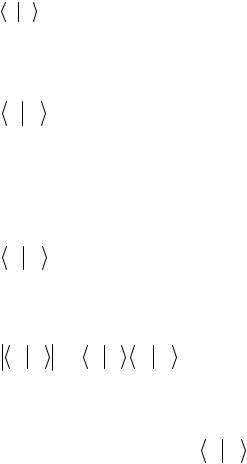
s
ϕ ψ = ∑ϕ jψ j
j =1 |
(1) |
|
В бесконечномерном гильбертовом пространстве l2 аналогичное определение имеет вид:
∞
ϕ ψ = ∑ϕ jψ j
j =1 |
(2) |
Наконец, если ψ (x) и ϕ (x) - комплексные
функции из пространства L2 , то их скалярное произведение есть:
ϕ ψ = ∫ϕ (x)ψ (x)dx
(3)
Покажем, что для любых векторов линейного пространства со скалярным произведением выполняется следующее неравенство КошиБуняковского:
ϕ ψ 2 ≤ ϕ ϕ ψ ψ
(4)
Для определенности, при проведении выкладок будем иметь ввиду функции из пространства L2 .
Предположим вначале, что ϕ ψ - действительное
число.
Пусть ξ - действительный параметр. Рассмотрим следующую заведомо неотрицательную функцию от ξ (эта
28
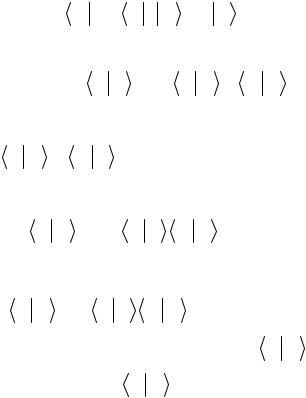
функция представляет собой интеграл от заведомо
неотрицательного выражения). |
|
) |
|
|
||||
F (ξ ) |
|
∫( |
|
)( |
|
|
|
|
= |
ψ (x) + ξϕ (x) |
ψ (x) + ξϕ |
(x) dx ≥ 0 |
(5) |
||||
|
В обозначениях Дирака имеем: |
|
|
|
||||
F(ξ ) |
|
|
|
|
||||
= |
(ψ + ξ ϕ )(ψ + ξ ϕ ) |
|
|
|
|
|||
|
В развернутой записи рассматриваемая функция |
|||||||
представляет собой квадратный трехчлен: |
|
|
||||||
F (ξ ) = ξ 2 ϕ ϕ + 2ξ ϕ ψ + ψ ψ |
|
(6) |
||||||
|
|
|
|
|
|
|
|
|
|
Здесь мы учли предположение о действительности |
|||||||
рассматриваемого |
скалярного |
произведения, |
т.е. |
|||||
ϕ ψ |
= ψ ϕ |
|
|
|
|
|
|
|
|
Условие |
неотрицательности |
означает, |
что |
||||
дискриминант меньше или равен нулю: |
|
|
|
|||||
4( ϕ ψ )2 − 4 ϕ ϕ ψ ψ ≤ 0 |
|
|
|
(7) |
||||
|
|
|
|
|
|
|
|
|
|
Таким образом в рассматриваемом случае |
|||||||
выполняется неравенство КошиБуняковского: |
|
|
||||||
( ϕ ψ )2 ≤ ϕ ϕ |
ψ ψ |
|
|
|
(8) |
|||
|
|
|
|
|
|
|
|
|
|
Предположим теперь, что |
ϕ ψ - |
комплексное |
|||||
число. |
|
Пусть |
ϕ ψ |
= r exp(iα ) , |
где |
r и |
α - |
|
действительные числа.
Введем функцию, отличающуюся от ϕ (x) только
фазой
29
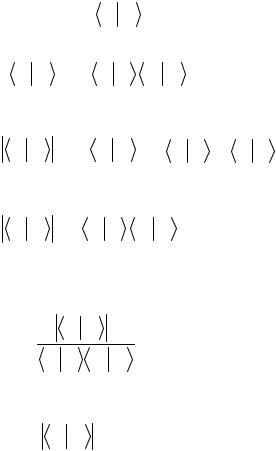
ϕ% (x) = ϕ (x)exp(iα )
|
Тогда |
% |
|
= r |
является действительным числом |
||||
|
ϕ ψ |
|
|||||||
и для него выполняется доказанное выше неравенство: |
|||||||||
% |
) |
2 |
≤ |
% % |
ψ ψ |
|
|||
( ϕ ψ |
|
ϕ ϕ |
|
||||||
|
Учтем, что введенное фазовое преобразование не |
||||||||
меняет |
|
модуля |
скалярного |
произведения, поэтому: |
|||||
ϕ ψ |
2 |
= |
( |
ϕ% ψ |
) |
2 |
% % |
ϕ ϕ |
|
|
|
|
|
|
, |
ϕ ϕ = |
|||
|
Таким образом, неравенство КошиБуняковского |
||||||||
выполняется и в общем случае: |
|
||||||||
ϕ ψ 2 |
≤ ϕ ϕ |
ψ ψ |
|
(9) |
|||||
|
|
|
|
|
|
|
|
|
|
|
Введем величину F , называемую согласованностью |
||||||||
(fidelity) квантовых состояний ϕ(x) и ψ (x). |
|||||||||
|
ϕ ψ 2 |
|
|
|
|
||||
F = ϕ ϕ ψ ψ |
|
|
|
(10) |
|||||
|
|
|
|
|
|
|
|
|
|
|
Для состояний, нормированных на единицу, имеем |
||||||||
просто: |
|
|
|
2 |
|
|
|
|
|
F = |
ϕ ψ |
|
|
|
|
(11) |
|||
|
|
|
|
|
|
|
|
|
|
|
Из неравенства КошиБуняковского следует, что |
||||||||
0 ≤ F ≤ 1 |
|
|
|
|
|
|
(12) |
||
|
Если исходить из этого неравенства, то заманчиво |
||||||||
предположить, что |
F задает некоторую вероятность. Так |
||||||||
30
