
Точность статистических оценок
.pdf
Точность статистических характеристик |
|
|
||
Неравенство КошиБуняковского |
|
|
|
|
Пусть Y =Y (x)и |
Z = Z (x)- |
действительные случайные |
величины, |
|
представляющие собой |
произвольные |
функции от координаты x . |
Пусть |
ξ - |
действительный параметр. Рассмотрим заведомо неотрицательную функцию от |
ξ |
|||
F (ξ)= ψ (ξY + Z )2 ψ ≥ 0 |
|
|
|
|
В развернутой записи рассматриваемая функция представляет собой квадратный трехчлен:
F (ξ)=ξ2 M (Y 2 )+2ξM (YZ )+ M (Z 2 )
Условие неотрицательности означает, что дискриминант меньше или равен нулю:
4 (M (YZ ))2 −4M (Y 2 )M (Z 2 )≤ 0
Таким образом для любых (коммутирующих) случайных величин выполняется неравенство КошиБуняковского:
(M (YZ ))2 ≤ M (Y 2 )M (Z 2 )
В частности, если в качестве случайных величин рассмотреть Y − M (Y ) и
Z − M (Z ), то для дисперсий получим неравенство:
DY DZ ≥ M ((Y − M (Y ))(Z − M (Z ))) 2 .
Из последнего выражения следует неравенство для коэффициента корреляции
r2 ≤1
Соотношение неопределенностей Гейзенберга для координаты и импульса
В приведенном выше примере рассмотрим вместо ξY + Z выражение ξ |
∂ |
+ x . |
|
∂x |
|||
|
|
|
∂ |
+ |
|
∂ |
|
||
Заметим, что оператор производной не является эрмитовым |
|
|
= − |
|
. Чтобы |
||
∂x |
∂x |
||||||
|
|
∂ |
|
|
|||
запись сделать более наглядной введем оператор импульса pˆ = −i |
|
. |
|
|
|||
|
|
|
|
||||
|
|
|
∂x |
|
|
||
Рассмотрим как и при выводе неравенства КошиБуняковского заведомо неотрицательную функцию от действительного параметра ξ
F ( |
|
) |
|
( |
i p x)(i p x) |
|
|
0 |
|
|
ξ |
|
= ψ |
|
− ξ ˆ + ˆ |
ξ ˆ + ˆ |
ψ |
≥ |
|
В развернутой записи имеем:
F (ξ)=ξ2 M (pˆ 2 )−iξM (pxˆ ˆ − xpˆ ˆ )+ M (xˆ2 )
Учтем каноническое коммутационное соотношение
pxˆ ˆ − xpˆ ˆ = −i
1
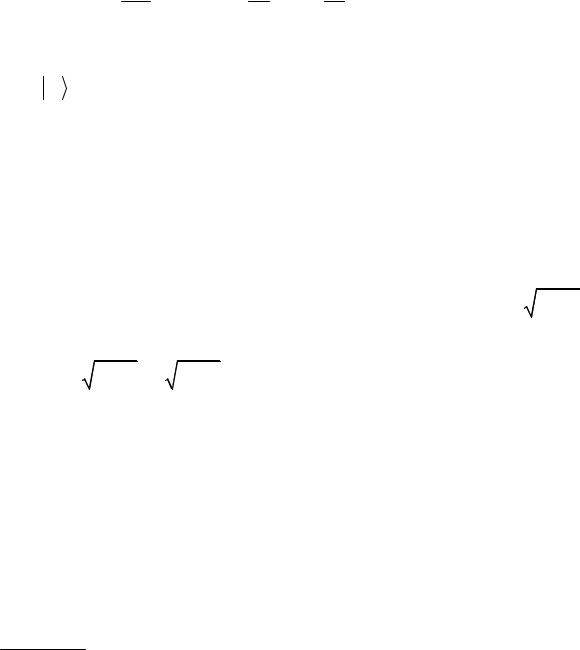
В качестве наблюдаемых рассмотрим величины xˆ − M (xˆ )и pˆ − M (pˆ ),
которые, очевидно, удовлетворяют тому же коммутационному соотношению. Тогда для произведения дисперсий координаты и импульса получим коммутационное соотношение
Dx Dp ≥ 14
Дисперсия импульса есть средний квадрат импульса минус средний импульс в квадрате:
Dp = M (pˆ 2 )−(M (pˆ ))2
В развернутой записи средний квадрат импульса очевидно есть:
M (pˆ 2 )= −∫ψ* (x)∂∂x22 ψ (x)dx = ∫∂∂xψ* (x)∂∂xψ (x)dx
Как следует из приведенных выкладок, неравенство обращается в равенство в том и только том случае, когда при некотором ξ :
(i p |
x) |
|
|
0 |
ξ ˆ |
+ ˆ |
ψ |
= |
|
Это равенство имеет место только для гауссова состояния (основного состояния гармонического осциллятора).
ψ (x)= |
1 |
|
exp − |
(x − μ)2 |
|
|||
(2πσ |
2 |
) |
4σ |
2 |
||||
|
|
|
||||||
|
|
1/ 4 |
|
|
|
|||
Здесь μ и σ2 - среднее и дисперсия для распределения координаты
Неравенство РаоКрамера
Рассмотрим систему, для которой псифункция действительна ψ (x)= P (x). Для такой системы средний импульс равен нулю, а квадрат импульса есть:
ˆ |
2 |
) |
= |
∫ |
∂ |
P |
(x) |
∂ |
|
P (x)dx |
= |
1 |
∫ |
(P′(x))2 |
dx |
|
|
|
|
|
|
|
|||||||||||
M (p |
|
|
∂x |
∂x |
|
4 |
P (x) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Здесь штрих означает производную по x . |
|
|
||||||||||||||
Введем информацию Фишера |
|
|
|
|
|
|
||||||||||
Ix = 4Dp = 4M (pˆ |
2 )= ∫ |
(P′(x))2 |
dx |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
P (x) |
|
|
|
|
|
|
Тогда соотношение неопределенностей запишется в виде неравенства РаоКрамера
Dx Ix ≥1
Выборочные статистики –это функции от выборки Выборочные среднее и дисперсияэто примеры статистик.
x = x1 +... + xn n
2
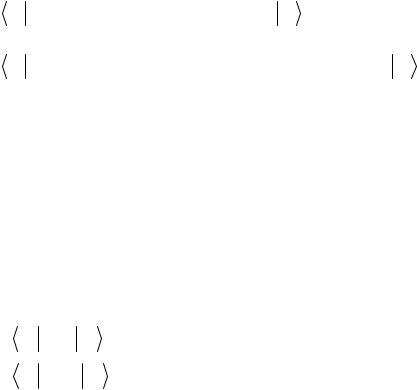
s2 = 1 ∑n (x − x )2
n n k =1 k
Будучи функцией от выборки, статистики представляют собой случайные величины.
Пусть θˆ - некоторая статистика. Ее распределение есть P (θˆ). Примеры.
Соотношение неопределенностей (неравенство РаоКрамера) в пространстве θˆ
Dθˆ Iθˆ ≥1
Неравенство РаоКрамера превращается в равенство (эффективная оценка) в том и только том случае, когда распределение статистики нормальное.
Многомерное соотношение неопределенности
Рассмотрим пространство размерности s .
Пусть xˆ j , pˆ j , j =1,..., s - соответствующие операторы координат и импульсов. Вывод соотношения неопределенности в многомерном случае аналогичен
одномерному, но теперь вместо действительного числа |
ξ следует ввести |
|
действительную симметричную матрицу Ξ |
с элементами |
ξjσ , j,σ =1,..., s . |
Введем также действительный вектор η (ηj |
j =1,..., s ). |
|
Рассмотрим следующее заведомо неотрицательное выражение (по повторяющимся индексам, как обычно, предполагается суммирование):
ξ |
= ψ η |
− |
ξ |
|
|
ˆ |
+ ˆ |
)(i |
ξ |
|
ˆ |
+ ˆ |
η |
ψ ≥ |
0 |
|
|
|
|
|
F( ) |
|
j ( i |
|
|
jσ pσ |
x j |
|
lρ pρ |
xl ) l |
|
|
|
|
|
||||||
В развернутом виде получим: |
|
|
|
|
|
|
|
|
) |
|
|
|||||||||
ξ |
= ψ η η ξ |
jσ |
ξ |
|
ˆ ˆ |
− |
|
ξ |
ˆ ˆ |
−ξ |
ˆ ˆ |
|
+ ˆ ˆ |
ψ ≥ |
0 |
|||||
F( ) |
|
j l ( |
|
|
lρ pσ pρ |
|
i( |
jρ pρ xl |
|
lρ x j pρ ) |
x j xl |
|
||||||||
Чтобы использовать фундаментальные коммутационные соотношения между координатой и импульсом, перепишем последнее выражение, осуществив замену
индексов j и l друг на друга, после чего сложим полученное выражение с исходным.
Вкачестве наблюдаемых будем использовать центрированные координаты и импульсы (имеющие нулевые средние).
Врезультате получим условие, согласно которому нижеследующее матричное выражение является неотрицательно определенным.
ΞΣp Ξ − Ξ + Σx ≥ 0
Здесь мы ввели матрицы ковариаций координат и импульсов. Элементы этих |
||||
матриц определяются выражениями |
||||
(Σx |
)jl = ψ xˆ j xˆl ψ |
|||
Σ |
)jl |
= ψ |
ˆ ˆ |
ψ |
( p |
|
p j pl |
|
|
Учтем неотрицательную определенность матрицы ковариаций импульсов, что позволяет определить квадратный корень из нее. Тогда, полученное выражение можно представить в виде:
3
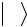
|
ΞΣ1/ 2 |
− |
1 |
Σ−1/ 2 |
|
Σ1/ 2 |
Ξ− |
1 |
Σ−1/ 2 |
|
− |
1 |
Σ−1 |
+Σ |
|
≥ 0 |
|
p |
|
2 |
p |
|
p |
|
2 |
p |
|
|
4 |
p |
|
x |
|
Первое слагаемое слева заведомо неотрицательно определено (и обращается в ноль
при Ξ = 1 |
Σ−p1 ). Отсюда следует, что и выражение |
− |
1 |
Σ−p1 |
+Σx неотрицательно |
|||
|
|
|
2 |
|
|
4 |
|
|
определено, т.е. |
|
|
|
|
||||
Σ |
x |
≥ |
1 |
|
|
|
|
|
4Σp |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
Из приведенных расчетов следует, что неравенство обращается в равенство в том и только том случае, когда вектор состояния удовлетворяет следующему условию
при Ξ = |
1 |
Σ−p1 : |
|
|
|
|
|
||||
(i |
|
|
|
2 |
|
|
|
|
|
|
|
ξ |
ˆ |
+ ˆ |
|
ψ = |
0 |
|
|
|
|
||
|
lρ pρ |
|
xl )l |
|
|
|
|
|
|||
Отсюда |
|
получаем, |
что соответствующее состояние |
является |
гауссовским с |
||||||
матрицей ковариаций в координатном представлении Σx |
= |
1 |
|
: |
|||||||
4Σp |
|
||||||||||
4
