
6.4 Використання теорії квадратичних форм
Основні поняття
З п. 3.4 відомо, що загальне рівняння кривої другого порядку має вигляд
![]() ,
(6.16)
,
(6.16)
де
![]()
![]() ,
,![]() ,
,![]() ,
,![]() – дійсні числа й, принаймні, один з
коефіцієнтів
– дійсні числа й, принаймні, один з
коефіцієнтів![]() відмінний від нуля. Це рівняння визначає
або вироджені лінії другого порядку:
уявні криві або порожню множину, точку,
прямі (пересічні або паралельні), або
невироджені: еліпс (коло), гіперболу,
параболу .
відмінний від нуля. Це рівняння визначає
або вироджені лінії другого порядку:
уявні криві або порожню множину, точку,
прямі (пересічні або паралельні), або
невироджені: еліпс (коло), гіперболу,
параболу .
З п.4.5.1 відомо, що загальне рівняння поверхні другого порядку має вигляд
![]() ,
(6.17)
,
(6.17)
де
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() – дійсні числа й, принаймні, один з
коефіцієнтів
– дійсні числа й, принаймні, один з
коефіцієнтів![]() відмінний від нуля. Це рівняння визначає
або вироджені поверхні другого порядку:
уявні поверхні або порожню множину,
точку, площини (пересічні, паралельні,
або що зливаються), або невироджені
поверхні: еліпсоїди, гіперболоїди,
параболоїди, циліндри, конуси, поверхні
обертання. Канонічні рівняння поверхонь
другого порядку досліджені раніше в
п.п.4.5.2 – 4.5.7 методом перетинів. Розглянемо
метод приведення рівнянь кривих і
поверхонь до канонічного вигляду, що
заснований на використанні теорії
квадратичних форм. (У рівняннях (6.16),
(6.17) для подальшого розуміння коефіцієнти
позначені іншими буквами).
відмінний від нуля. Це рівняння визначає
або вироджені поверхні другого порядку:
уявні поверхні або порожню множину,
точку, площини (пересічні, паралельні,
або що зливаються), або невироджені
поверхні: еліпсоїди, гіперболоїди,
параболоїди, циліндри, конуси, поверхні
обертання. Канонічні рівняння поверхонь
другого порядку досліджені раніше в
п.п.4.5.2 – 4.5.7 методом перетинів. Розглянемо
метод приведення рівнянь кривих і
поверхонь до канонічного вигляду, що
заснований на використанні теорії
квадратичних форм. (У рівняннях (6.16),
(6.17) для подальшого розуміння коефіцієнти
позначені іншими буквами).
Загальне рівняння кривої (6.16) і загальне рівняння поверхні (6.17) включають квадратичну й лінійну форми.
У рівнянні (6.16):
квадратична
форма –
![]() з матрицею
з матрицею ;
лінійна –
;
лінійна –![]() .
.
У рівнянні (6.17):
квадратична
форма –
![]() з матрицею
з матрицею
 ;
лінійна –
;
лінійна –![]() .
.
Таким чином, рівняння (6.16), (6.17) можна записати у вигляді
![]() .
(6.18)
.
(6.18)
Схема приведення загального рівняння другого порядку до канонічного вигляду
Для приведення загального рівняння (6.18) до канонічного вигляду треба виконати наступні операції.
Привести квадратичну форму
 до канонічного вигляду методом
до канонічного вигляду методом
ортогональних перетворень.
1.1 Скласти
характеристичне рівняння
![]() й знайти його корені – власні числа
й знайти його корені – власні числа![]() ,
,![]() для кривої (
для кривої (![]() ,
,![]() ,
,![]() – власні числа для поверхні).
– власні числа для поверхні).
1.2 Знайти власні вектори, які відповідають власним числам.
1.3 Виписати
матрицю переходу
![]() від базису
від базису![]() (
(![]() )
до ортонормованого базису
)
до ортонормованого базису![]() змінних
змінних![]() ,
,![]() (
(![]() змінних
змінних![]() ,
,![]() ,
,![]() ),
що складена із власних векторів
(координати власних векторів записуються
в стовпці матриці переходу).
),
що складена із власних векторів
(координати власних векторів записуються
в стовпці матриці переходу).
1.4 Записати
квадратичну форму
![]() в
канонічному вигляді
в
канонічному вигляді
![]() (
(![]() ).
).
2. Виконати
перетворення
![]() над лінійною формою
над лінійною формою
![]() .
(Після виконання п.1.1 і п.1.2 рівняння
кривої та поверхні набудуть відповідно
вигляду
.
(Після виконання п.1.1 і п.1.2 рівняння
кривої та поверхні набудуть відповідно
вигляду
![]()
![]()
При цьому вільний член залишається без змін).
3. Виділити повні квадрати щодо нових змінних.
4.
Здійснити паралельний перенос осей
координат, переходячи до нових змінних
![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() ).
).
5. Записати загальне рівняння в канонічному вигляді.
6. Виразити
канонічні змінні
![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() )
через початкові змінніx,
y
(x,
y,
z).
Для цього спочатку треба виразити змінні
)
через початкові змінніx,
y
(x,
y,
z).
Для цього спочатку треба виразити змінні
![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() )
через початкові за формулою
)
через початкові за формулою![]() ,
а потім з формул паралельного переносу
осей координат одержати вираз канонічних
через початкові.
,
а потім з формул паралельного переносу
осей координат одержати вираз канонічних
через початкові.
Приклад.
Привести до канонічного
вигляду рівняння кривої
![]() та виразити канонічні змінні через
початкові змінні.
та виразити канонічні змінні через
початкові змінні.
Розв'язання.
1.1. Матриця квадратичної
форми
![]() має вигляд
має вигляд![]() .
.
Складемо характеристичне
рівняння
![]() :
:
![]()
![]() ,
корні якого
,
корні якого
![]() ,
,![]() .
.
1.2. Для визначення власних векторів складемо систему

Покладемо послідовно
![]() ,
,![]() .
.
![]() :
:

Тоді
![]() – власний вектор,
– власний вектор,![]() – нормований власний вектор.
– нормований власний вектор.
![]() :
:

Тоді
![]() – власний вектор,
– власний вектор,![]() – нормований власний вектор.
– нормований власний вектор.
Отримали нову систему
координат
![]() поворотом старої системи
поворотом старої системи![]() на відповідний кут.
на відповідний кут.
1.3. Запишемо матрицю переходу
![]() від базису
від базису![]() до ортонормованого базису
до ортонормованого базису![]() змінних
змінних![]() ,
,![]() :
:
 .
.
1.4. Квадратична форма
![]() набуде канонічного вигляду
набуде канонічного вигляду
![]() .
.
2. Виконаємо перетворення
лінійної форми
![]() .
Через те, що
.
Через те, що![]() ,
тобто
,
тобто ,
то
,
то
Підставимо отримані формули перетворення в лінійну форму
![]() .
.
Через те, що вільний член не
змінюється, то рівняння кривої в змінних
![]() ,
,![]() має вигляд
має вигляд
![]() .
.
Виділимо повний квадрат за змінною
 :
:
![]()
![]() ,
,
 .
.
4. Виконаємо паралельний
перенос осей координат
![]() ,
,![]() .
Покладемо
.
Покладемо![]() ,
,![]() ,
що відповідає переносу початку координат
в точку
,
що відповідає переносу початку координат
в точку![]() .
.
5. Запишемо загальне рівняння кривої в канонічному вигляді
![]() .
.
Отримали канонічне рівняння
еліпсу в системі координат
![]() .
.
6. Виразимо
канонічні змінні
![]() ,
,![]() через
початкові
через
початкові![]() .
Для цього спочатку знайдемо
вираз змінних
.
Для цього спочатку знайдемо
вираз змінних
![]() ,
,![]() через початковіx,
y
за формулою
через початковіx,
y
за формулою
![]() :
:
 ,
,
тобто
![]() ,
,![]() .
Тоді
.
Тоді![]() ,
,![]() .
.
Відповідь. Еліпс
![]() ,
,![]() ,
,![]() .
.
Приклад.
Привести до канонічного вигляду рівняння поверхні
![]() ,
,
та виразити канонічні змінні через початкові змінні.
Розв'язання.
1.1. У системі координат
![]() матриця квадратичної форми
матриця квадратичної форми
![]()
має вигляд
 .
Складемо характеристичне рівняння
.
Складемо характеристичне рівняння
![]() :
:
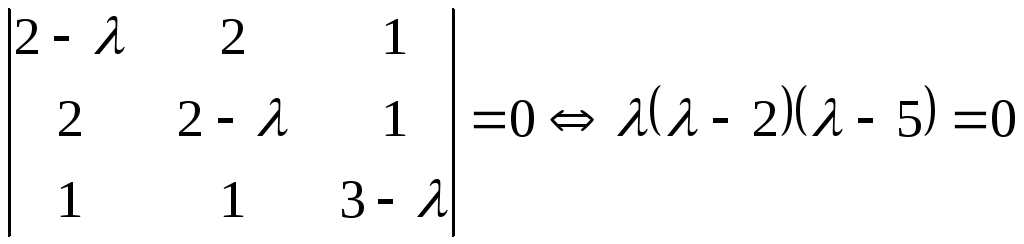 .
.
Тоді
![]() ,
,![]() ,
,![]() – власні значення.
– власні значення.
1.2. Для визначення власних векторів складемо систему

Покладемо послідовно
![]() ,
,![]() ,
,![]() .
.
![]() :
:
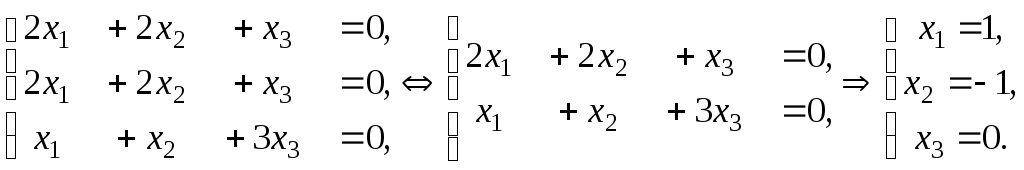
Тоді
![]() – власний вектор,
– власний вектор,![]() – нормований власний вектор.
– нормований власний вектор.
![]() :
:

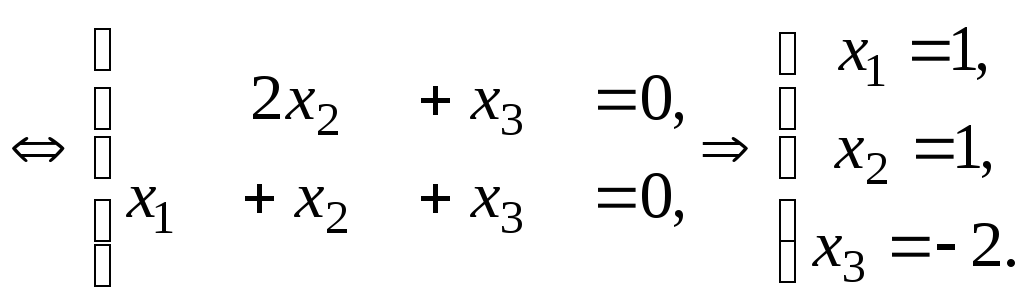
Тоді
![]() – власний вектор,
– власний вектор,![]() – нормований власний вектор.
– нормований власний вектор.
![]() :
:

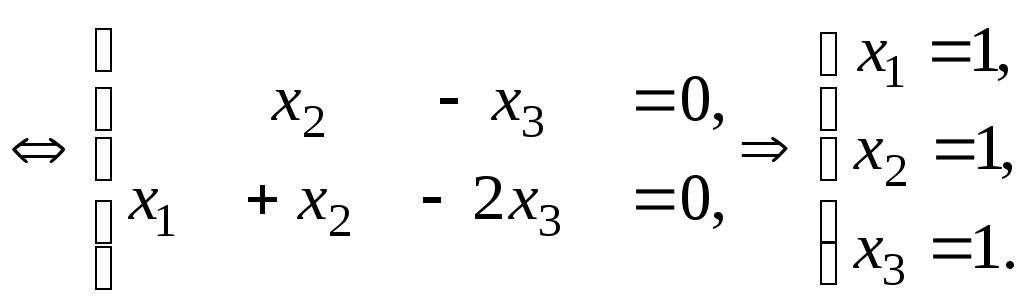
Тоді
![]() – власний вектор,
– власний вектор,![]() – нормований власний вектор.
– нормований власний вектор.
Отримали ортонормовану
систему векторів
![]() .
.
1.3. Запишемо матрицю переходу
![]() від базису
від базису![]() до ортонормованого базису
до ортонормованого базису![]() змінних
змінних![]() ,
,![]() ,
,![]() :
:
 .
.
1.4. Квадратична форма
![]() набуде канонічного вигляду
набуде канонічного вигляду
![]() .
.
2. Виконаємо перетворення
лінійної форми
![]() .
Через те, що
.
Через те, що![]() ,
тобто
,
тобто
 ,
то
,
то
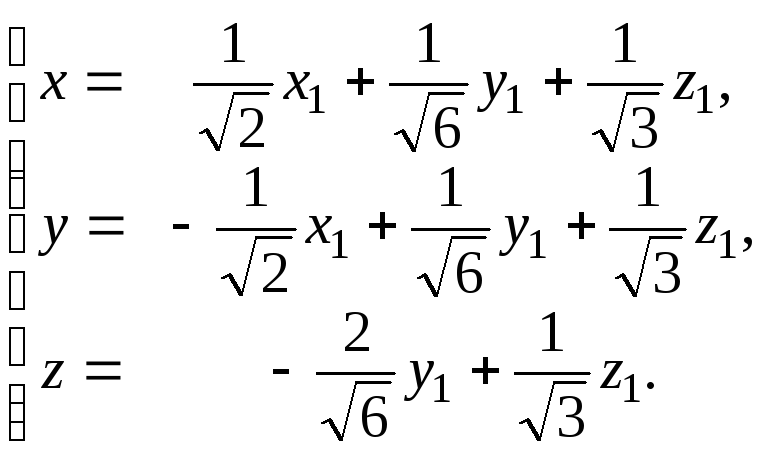
Підставимо отримані формули
перетворення в лінійну форму
![]() :
:
![]()
![]() .
.
Через те, що вільний член не
змінюється, то рівняння поверхні в
змінних
![]() ,
,![]() ,
,![]() має
вигляд
має
вигляд
![]() .
.
3. Виділимо повний квадрат за
змінною
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
 .
.
4. Виконаємо паралельний
переніс осей координат
![]() ,
,![]() ,
,![]() .
Покладемо
.
Покладемо![]() ,
,![]() ,
,![]() ,
що відповідає переносу початку координат
у точку
,
що відповідає переносу початку координат
у точку![]() .
.
5. Запишемо загальне рівняння
поверхні в канонічному вигляді
![]() .
Отримали канонічне рівняння еліптичного
параболоїда в системі координат
.
Отримали канонічне рівняння еліптичного
параболоїда в системі координат![]() .
.
6. Виразимо канонічні змінні
![]() ,
,![]() ,
,![]() через початкові
через початкові![]() .
Для цього спочатку
знайдемо вираз змінних
.
Для цього спочатку
знайдемо вираз змінних
![]() ,
,![]() ,
,![]() через початкові змінніx,
y, z
за формулою
через початкові змінніx,
y, z
за формулою
![]() :
:
 ,
,
тобто
![]() ,
,![]() ,
,![]() .
Тоді
.
Тоді
![]() ,
,
![]() ,
,![]() .
.
Відповідь. Еліптичний
параболоїд
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Контрольні завдання
1. Запишіть загальне рівняння кривої другого порядку на площині. Як привести загальне рівняння кривої другого порядку до канонічного вигляду?
2. Запишіть загальне рівняння поверхні другого порядку. Як привести загальне рівняння поверхні другого порядку до канонічного вигляду?
