6.2 Власні числа та власні вектори оператора. Самоспряжені оператори

Власні числа та власні вектори

Якщо існує такий ненульовий елемент , що

, (6.4)

то він називається власним вектором оператора , а число– його власним числом (значенням). Таким чином, дія оператора на власний вектор дає той само вектор, помножений на власне число. Аби знайти ці вектори і числа, перепишемо (6.4) у вигляді , або

. (6.5)

Згідно з теоремою про обернений оператор такому рівнянню задовольнятиме ненульовий вектор тоді і тільки тоді, коли оператор не матиме оберненого. З цього випливає, що і його матриця не матиме оберненої, критерієм чого є рівність нулю її визначника, тобто

. (6.6)

Отже, власне число має бути коренем рівняння (6.6). Це алгебраїчне рівняння ступеня називаєтьсяхарактеристичним рівнянням оператора . Відповідно до основної теореми алгебри алгебраїчне рівняння ступенямаєкоренів, серед яких можуть бути і кратні корені, і комплексні корені.

Теорема. Характеристичні рівняння для одного і того ж оператора в різних базисах еквівалентні.

Доведення.

Дійсно, нехай матриці оператора в двох різних базисах будуть, відповідно,і, і нехай– матриця переходу від одного базису до іншого. Тоді, згідно з правилами перетворення матриці оператора, маємо

Теорему доведено.

Для кожного власного числа рівняння (6.5) визначає власний вектор

.

Приклад.

Знайти власні числа тa вектори оператора, матриця якого в деякому базисі має вигляд .

Розв'язання.

Маємо . Характеристичне рівняння. Корені рівняння будуть.

Тепер знайдемо власні вектори.

Для власний вектор буде розв’язком системи рівнянь

Звідси маємо

.

де – довільне число.

Для числа власний вектор буде розв’язком системи рівнянь

, або

Звідси маємо, що

,

де – довільне число.

Для числа власний вектор відрізнятиметься знаком перед уявною одиницею.

Приклад.

Знайти власні числа і вектори оператора проектування на площину, якщо його матриця: .

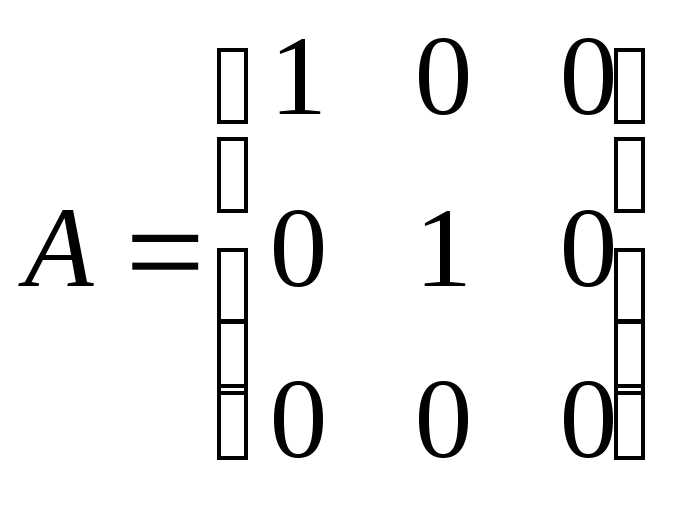Розв'язання.

Характеристичне рівняння має корені,.

Власні вектори:

Приклад.

Знайти власні числа і вектори оператора повороту на кут навколо осі, якщо матриця оператора.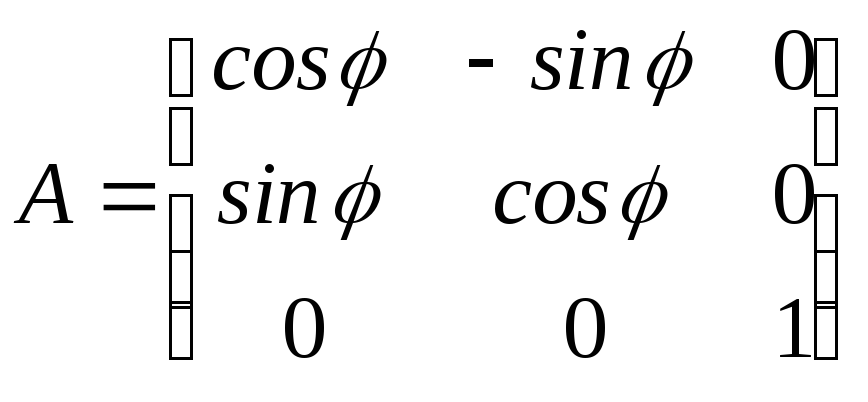

Розв'язання.

Характеристичне рівняння

має корені .

Власні вектори:

Власні вектори і числа оператора є дуже важливими його характеристиками. Особливого значення надають цьому такі дві теореми.

Теорема. Власні вектори оператора, які відповідають різним власним числам, – лінійно незалежні.

Доведення.

Хай оператор має власні числаі відповідні їм власні вектори. Хай всі власні числа різні,. Використаємо метод математичної індукції. Один вектор завжди лінійно незалежний. Хай теперлінійно незалежні. Доведемо, що ілінійно незалежні. Для цього припустимо, що це не так, тобто припустимо, що існують такі числа, з-поміж яких є і ненульові, що

. (6.7)

Подіємо спочатку на (6.7) оператором

. (6.8)

Тепер помножимо (6.7) на і віднімемо від (6.8)

.

Оскільки всі ,то із лінійної незалежності векторіввипливає, що. Але тоді із (6.7) випливає, що і, тобто рівняння (6.7) можливе тільки у тому разі, коли всі коефіцієнти дорівнюють нулю, а це означає, що всі вектори лінійно незалежні.

Теорему доведено.

Теорема. Матриця оператора в базисі з власних векторів має діагональний вигляд.

Доведення.

Хай набір власних векторів операторадостатній для того, щоб утворювати базис. Знайдемо матрицю оператора. Для цього подіємо на кожний базисний вектор, який до того ж є і власним, оператором

Звідси маємо діагональну матрицю

,

по діагоналі якої стоять власні числа оператора.

Теорему доведено.

Висновок.

Якщо оператор маєрізних власних чисел, то в деякому базисі, а саме,в базисі з власних векторів, матриця цього оператора має діагональний вигляд.

Спряжені та самоспряжені оператори

Розглянемо евклідовий простір (лінійний простір, в якому введений скалярний добуток). Два оператори іназиваютьсяспряженими, якщо

, (6.9)

де і– довільні елементи простору. Спряжений оператор позначають.

Властивості спряженого оператора

1. .

2. .

3. .

4. .

5. .

Доведення.

Доведемо останню властивість.

Маємо, згідно з (6.9), . Застосовуючи (6.9) послідовно для кожного оператора, одержимо результат

.

Прирівнюючи праві частини, одержимо властивість 5. Що й потрібно було довести.

Знайдемо тепер матрицю спряженого оператора в ортонормованому базисі. Хай дія операторів на вектори запишеться так

, .

Тоді для скалярних добутків одержимо

. (6.10)

. (6.11)

Прирівнюючи (6.10) і (6.11) згідно з (6.9), маємо

, (6.12)

тобто матриця спряженого оператора є транспонованою матрицею оператора.Звідси, зокрема, випливає, що .

Оператор називається самоспряженим, якщо , тобто

.

Для самоспряженого оператора матриця симетрична, , що зразу ж випливає з (6.12).

Зауваження.

Для того щоб виписати матрицю оператора, слід взяти до уваги, що матриця самоспряженого оператора симетрична, отже, коефіцієнти у квадратичній формі при перехресних добутках координат треба брати вдвічі меншими, бо

.

Приклад.

Довести, що оператор , де, самоспряжений.

Розв'язання.

Перевіримо безпосередньо:

;

.

Приклад.

Хай у просторі многочленів не вище другого ступеня, елементи якого мають вигляд , скалярний добуток визначено як , де . Довести, що оператор самоспряжений, якщо дія оператора – зміна знака в аргументі –.

Розв'язання.

Через те, що

,

,

оператор самоспряжений.

Приклад.

Довести, що оператор проектування на площину самоспряжений, якщо у базисійого матриця.

Розв'язання.

Через те, що то. Отже, оператор– самоспряжений.

В ортонормованому базисі скалярний добуток

має вигляд квадратичної форми, де коефіцієнти – елементи матриці оператора. Якщо матриця має діагональний вигляд, то квадратична форма набуває канонічного вигляду

,

де – діагональні елементи матриці оператора.

Очевидно, що в базисі з власних векторів оператора квадратична форма матиме канонічний вигляд, причому коефіцієнтами будуть власні числа оператора.

Для самоспряжених операторів дуже велике значення має наступна теорема.

Теорема. Самоспряжений оператор у -вимірному просторі маєдійснихвласних чисел, яким відповідають взаємно ортогональні власні вектори.

Дія самоспряженого оператора зводиться до розтягування або стискання вздовж напрямків, які задаються власними векторами. Дійсно, хай власні вектори утворюють базис. Тоді розкладання векторау цьому базисі матиме вигляд . Дія оператора дасть результат

,

звідки видно, що координати образу вектора змінились уразів.

Приклад.

Хай оператору деякому базисі тривимірного простору породжує квадратичну фор-

му . Знайти базис, в якому квадратична форма матиме канонічний вигляд, і виписати її.

Розв'язання.

Враховуючи наведені раніше зауваження, матриця оператора матиме вигляд

.

Тоді її характеристичне рівняння виглядає наступним чином

Власні числа: ,.

Власні вектори:

1) якщо , то

нормований вектор ;

2) якщо , то

нормований вектор ;

3) якщо , то

нормований вектор .

В зв’язку з тим, що всі власні числа різні вектори лінійно незалежні і утворюють базис. Легко перевірити, що він ортонормований. Матриця переходу до цього базису має вигляд

.

Матриця оператора в новому базисі

має діагональний вигляд, де на діагоналі стоять власні числа. Квадратична форма в новому базисі має канонічний вигляд , де координати вектора в старому і новому базисі пов’язані формулами:

Контрольні запитання та завдання

1. Дайте визначення власних векторів та власних чисел оператора.

2. Яке рівняння називається характеристичним?

3. Доведіть теорему про лінійно незалежні власні вектори оператора.

4. Які оператори називаються спряженими?

5. Доведіть теорему про діагональність матриці оператора.

6. Сформулюйте теорему про власні числа самоспряженого оператора.