6.3 Ортогональні оператори. Квадратичні форми

Ортогональні оператори

Оператор називаєтьсяортогональним, якщо задовольняє співвідношення

. (6.13)

Оскільки скалярний добуток визначає кути між елементами, то (6.13) означає, що ортогональний оператор не змінює кути між елементами. До речі, ортогональний базис такий оператор переводить знову в ортогональний.

Якщо (6.13) переписати як

,

то одержимо друге визначення ортогонального оператора

, або. (6.14)

Звідси маємо для матриці ортогонального оператора

, або. (6.15)

Зокрема, рівність (6.15), записана за елементами

,

свідчить, що рядки (стовпці) матриці ортогонального оператора – ортогональні.

Властивості ортогонального оператора

1. Якщо – ортогональний, то і – ортогональний.

2. Добуток двох ортогональних операторів також є ортогональним оператором.

3. .

4. Квадрат власного числа оператора дорівнює одиниці.

Доведення.

1. Згідно з (6.14) маємо .

2. .

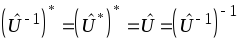3. Дійсно, . З іншого боку маємо

.

4. Хай – власний вектор ортогонального оператора, а – власне число. Тоді .

Приклад.

Описати дію ортогонального оператора у двовимірному просторі.

Розв'язання.

Хай . Із рівностізнаходимо, абоЗвідси маємо, що. Хай. Тоді маємо два типи матриць:.

Матриця визначає поворот на кутпроти годинникової стрілки. Матриця– поворот і відбиття щодо осіОх, бо її можна записати як , де– матриця оператора відбиття щодо осі х.

Квадратичні форми

У попередньому розділі йшлося про квадратичні форми, які за допомогою самоспряженого оператора визначаються в ортонормованому базисі як

,

де – елементи матриці оператора , яка називається також матрицею квадратичної форми. Слід зауважити, що ця матриця симетрична,, оскільки операторсамоспряжений. У базисі із власних векторів оператора квадратична форма приймаєканонічний вигляд

,

де – власні числа оператора, – координати елемента у базисі із власних векторів.

Приклад.

Знайти базис, у якому квадратична форма має канонічний вигляд.

Розв'язання.

Матриця форми: . Власні числа знаходимо з рівняння

. Звідси маємоВласні вектори знаходимо з системи.

Маємо . Матриця переходу.

Матриця квадратичної форми в новому базисі: .

Канонічний вигляд форми .

Теорема. Якщо визначник симетричної матриці не дорівнює нулю, то всі власні числа матриці відмінні від нуля.

Доведення.

Дійсно, завжди знайдеться базис, у якому матриця прийме діагональний вигляд, причому діагональними елементами будуть власні числа. Тоді маємо, що . Але.

Теорему доведено.

Класифікація квадратичних форм

1. Якщо всі власні числа більше нуля, , то квадратична форма –строго додатньо означена.

Дійсно

.

2. Якщо всі , то квадратична форма –строго від’ємно означена, тобто

.

3. Якщо , то квадратична форма –додатно означена. Причому вздовж напрямку, який задається власним вектором , що відповідає нульовому власному числу , квадратична форма дорівнює нулю, тобто .

4. Якщо , то квадратична формавід’ємно означена.

5. Якщо власні числа мають різні знаки, то квадратична форма неозначена. Це означає, що вздовж одних векторів вона додатна, а вздовж інших – від’ємна.

Для квадратичних форм справедливий закон інерції: якщо квадратична форма приводиться до канонічного вигляду в двох різних базисах, то число додатних і від’ємних членів буде одне і те ж.

Критерій Сільвестра

Класифікацію квадратичних форм зручно проводити за допомогою критерію Сільвестра, який полягає у такому.

Визначимо у матриці квадратичної форми

кутові визначники:

, ….

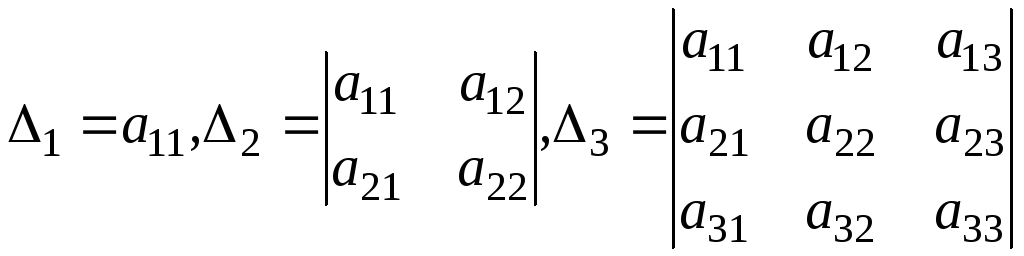Тоді:

1) якщо всі – квадратична форма строго додатно означена;

2) якщо , тобто, то квадратична форма строго від’ємно означена;

3) якщо у попередніх двох випадках визначники дорівнюють нулю, то квадратична форма просто додатно або від’ємно означена;

4) у всіх останніх випадках квадратична форма неозначена.

Приклад.

Визначити квадратичну форму .

Розв'язання.

Її матриця дорівнює . Кутові визначникиФорма неозначена.

Контрольні запитання та завдання

1. Дайте визначення ортогонального оператора.

2. Доведіть властивість ортогональності рядків (стовпців) матриці ортогонального оператора.

3. Чому дорівнюють власні числа ортогонального оператора?

4. Дайте визначення квадратичної форми.

5. Як знайти канонічний вигляд квадратичної форми?

6. Наведіть класифікацію квадратичних форм.

7. Сформулюйте закон інерції квадратичних форм.

8. Сформулюйте критерій Сільвестра.