5 Лінійні простори

У множинах математичних об’єктів можна ввести дві лінійні операції, а саме: додавання та множення на число, які мають властивості, загальні для всіх цих об’єктів. Це дозволяє сформулювати нове поняття – поняття лінійного простору. Лінійний простір, у якому введений скалярний добуток елементів, називається евклідовим простором. Поняття скалярного добутку і назву ввів У. Гамільтон у 1853 р. Термін внутрішній добуток застосував Г. Грасманн (1864 р.) (Grassmann H., 1809–1877 р.р., Німеччина). Позначення вперше зустрічається в О. Хенрічі (1903 р.), - у Дж. Гіббса в 1881 р. (Gibbs J.W., 1839-1903 рр., США). Використовуватиметься нерівність Коші-Буняковського (Коші довів нерівність для одного випадку в 1821 р., Буняковський (Буняковський В.Я., 1804-1889 р.р., Росія) у 1859 р.)

5.1 Лінійні простори. Базис. Вимірність. Ізоморфізм просторів

Поняття лінійного простору

Множина елементів, у якій введені операції додавання двох елементів та множення елемента на число, які не виводять за межі цієї множини та задовольняють властивості додавання матриць та множення матриці на число, називається лінійним простором. Елементи лінійного простору називають також векторами.

Розглянемо множину А елементів , в якій визначено дві операції:додавання двох елементів, , та множення елемента на число,, причому кожна з цих операцій дає елемент, який належить тій самій множині (кажуть, не виводить за межі множини). Хай ці операції підкоряються таким самим правилам, як і звичайні операції додавання та множення дійсних чисел, тобто:

1) ;

2) ;

3) (тобто в множині А є нульовий елемент);

4) , (тобто в множині для кожного елементає протилежний елемент);

5) ;

6) ;

7) ;

8) .

Така множина називається лінійним простором.

Приклади лінійних просторів.

1. Множини дійсних чисел R , або комплексних чисел С, якщо в них введені звичайні операції додавання та множення. Але, наприклад, множина додатних чисел не утворює лінійного простору щодо звичайних операцій додавання та множення, бо в цьому разі немає протилежного числа (воно має бути від’ємним, а, отже, не належатиме цій множині). Проте можна і на цій множині побудувати лінійний простір, якщо ввести операції додавання та множення інакше, а саме: сумою двох елементів називатимемо добуток двох додатних чисел, , ( означає елемент множини, а х – відповідне йому додатне число), а добутком елемента на число є елемент. Як видно, кожна з цих операцій дає додатне число, тобто не виводить за межі множини додатних чисел, і всі вісім перерахованих правил виконуються, якщо нульовим елементом визначити 1, а протилежним – зворотне число,. Дійсно, тоді,. Також легко перевіряється, що, .

2. Множина геометричних векторів (направлених відрізків), якщо суму двох векторів визначити за допомогою правила паралелограма, а множення вектора на числояк колінеарний вектор, довжина якого дорівнює, а напрямок співпадає, якщоабо протилежний, якщо. Але множина векторів, з якої вилучені вектори, колінеарні заданій прямій, не утворює лінійного простору, бо завжди можна знайти такі два вектори, які в сумі дадуть вектор, колінеарний цій прямій, тобто сума не належатиме множині.

3. Множина матриць заданого розміру, якщо додавання матриць та множення на число робити за правилами, що були викладені у п.1.2.

4. Множина розв’язків однорідної системи лінійних алгебраїчних рівнянь , деА – матриця , – стовпець п невідомих. Якщо r(A)<n, то це система невизначена і має безліч розв’язків. Суму двох розв’язків і добуток розв’язку на число визначатимемо за допомогою правил дій над матрицями. Тоді, якщо та– розв’язки, то– також розв’язок системи. Якщо – розв’язок, то – також розв’язок. Дійсно,

;

.

Неважко перевірити, що всі вісім правил додавання та множення на число виконуються. Таким чином, множина розв’язків однорідної системи лінійних алгебраїчних рівнянь утворює лінійний простір.

Базис та вимірність лінійного простору

Розглянемо k елементів лінійного простору L: . Згадаємо поняття лінійної залежності елементів. Якщо знайдуться такі числа, з яких хоча б одне відмінне від нуля, а лінійна комбінація елементів дорівнює нулю, тобто

,

то такі елементи називаються лінійно залежними. Якщо ж таких чисел немає, то елементи називаються лінійно незалежними. Максимальне число лінійно незалежних елементів цього простору називається його вимірністю і позначається як dimL.

Хай k елементів лінійно залежні, і хай, наприклад, . Тоді можна написати

.

У цьому разі кажуть, що подано у вигляді лінійної комбінації за елементами .

Хай тепер у лінійному просторі знайшлись п лінійно незалежних елементів таких, що будь-який елемент цього простору можна розкласти за цими елементами

.

Такий набір елементів називається базисом лінійного простору. Числа називаютьсякоординатами елемента у даному базисі . Запис

означає задавання елемента своїми координатами в цьому базисі. Якщо вибрати другий базис, , то той самий елемент матиме інші координати:, тобто

.

Теорема. Число елементів базису дорівнює вимірності лінійного простору.

Доведення.

1. Хай – базис лінійного простору. Це означає, що ці елементи лінійно незалежні, і до того ж для будь-якого елемента можна написати

, або .

Таким чином, доповнення системи базисних елементів ще одним, довільним, елементом дає вже систему лінійно залежних елементів (у крайньому разі, множник при дорівнює ). Звідси маємо, що число елементів базису– це максимально можливе число лінійно незалежних елементів і тому воно дорівнює вимірності простору.

2. Хай вимірність простору дорівнює п. Це означає, що максимальне число лінійно незалежних елементів дорівнює п. Якщо до цих елементів додати ще будь-який елемент , то одержимо вже систему лінійно залежних елементів

.

При цьому , бо в іншому разі елементибудуть лінійно залежні. З цього випливає, що для будь-якого елемента справедливий розклад

,

тобто – базис, і число елементів в ньому дорівнює п.

Теорему доведено.

Приклади.

1. Множина рядків , яка утворює лінійний простір щодо операцій додавання матриць та множення матриці на число. Розглянемо систему елементів цього простору.

;

;

.

Вона лінійно незалежна, бо ранг матриці, складеної з цих рядків, дорівнює їх кількості. Легко перевірити, що для будь-якого елемента

,

тобто базис простору рядків,п – вимірність цього простору, а числа – координати елементау цьому базисі.

2. Розглянемо однорідну систему лінійних алгебраїчних рівнянь щодоп невідомих. Хай . Визначимовільних невідомихі знайдемо множину розв’язків системи

Елемент цієї множини можна записати у вигляді стовпців

,

де перші k елементів виражаються через елементи , тобто, якщо, то розв’язок системи матиме вигляд

.

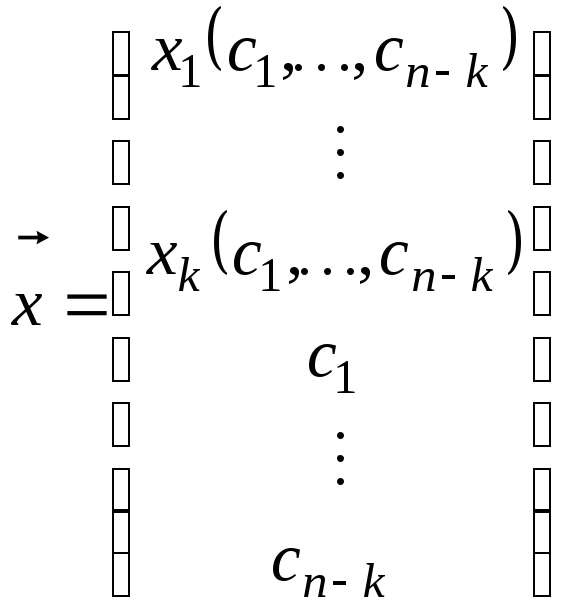Для чисел братимемо значення з рядків матриці розміром

.

Тоді одержимо розв’язків цієї системи

, ,.

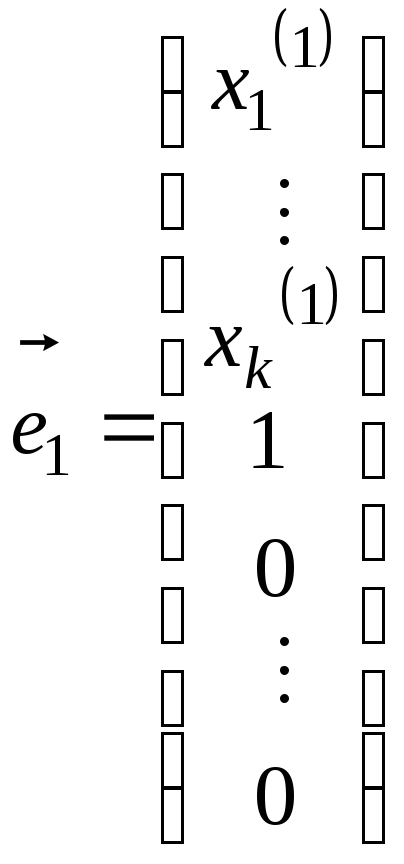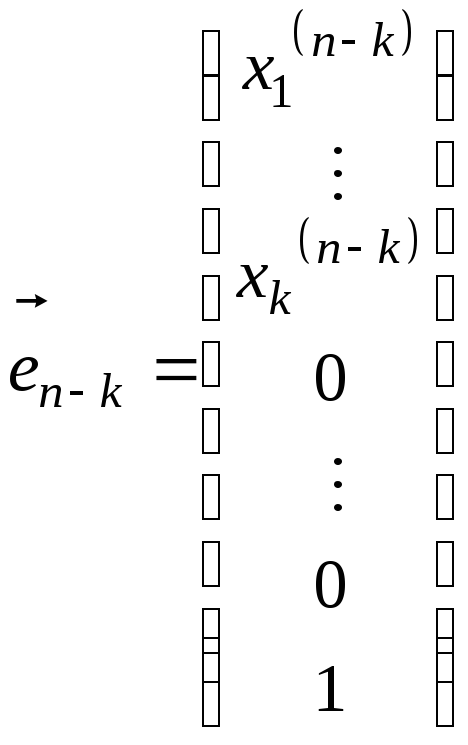Вони незалежні через те, що ранг матриці, складеної з цих стовпців, дорівнює . Очевидно, довільний розв’язок системи запишеться як

,

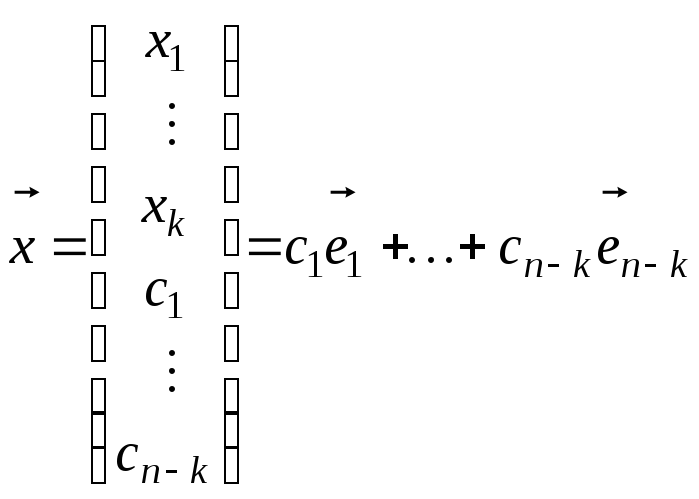тобто утворюють базис простору розв’язків однорідної системи лінійних алгебраїчних рівнянь. Вимірність цього простору дорівнює. Згадуючи, щоце можна записати як

3. Лінійний простір із геометричних векторів, колінеарних заданій прямій. Виберемо на цій прямій який-небудь вектор . Тоді будь-який вектор із даної множини можна записати як(рис. 5.1).

Рисунок 5.1

Таким чином, – базис, вимірність простору дорівнює 1.

4. Лінійний простір геометричних векторів, паралельних заданій площині.

Виберемо два неколінеарних вектори ,. Будь-який вектор можна записати як. Це видно із рис. 5.2.

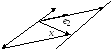
Рисунок 5.2

Відтак, ,– базис, вимірність простору дорівнює 2.

5. Множина просторових геометричних векторів утворює тривимірний простір, і будь-які три вектори, що не лежать в одній площині (некомпланарні) складають базис.

Наслідок.

Будь-які чотири геометричні вектори лінійно залежні.

Ізоморфізм лінійних просторів

Хай маємо два лінійних простори: Е, елементи якого позначимо ;R – елементи позначимо .

Хай між ними є взаємно-однозначна відповідність, тобто кожному відповідає один елементі навпаки.

Припустимо тепер, що відповідність між просторами така, що з відповідності івипливає відповідністьі, тобто елементу, помноженому на число, відповідає елемент, помножений на те ж число, а сумі елементіввідповідає сума їм відповідних елементів. Тоді такі два простори називаютьсяізоморфними. Як лінійні простори, вони еквівалентні, незалежно від елементів, з яких вони утворені.

Теорема. Для того щоб два простори були ізоморфні, необхідно і достатньо, аби вони мали однакову вимірність.

Висновок.

Всі простори однакової вимірності ізоморфні. Тобто як лінійні простори вони мають однакові властивості. Це означає, що можна вивчати властивості якогось одного простору цієї вимірності. Найзручніше вивчати простір рядків – так званий арифметичний лінійний простір.

Означення підпростору

Хай множина А утворює лінійний простір Е. Якщо підмножина щодо тих самих операцій сама утворює лінійний простірR, то він називається підпростором простору Е. Очевидно .

Приклади.

1. Множина дійсних чисел утворює підпростір простору комплексних чисел.

2. Множина рядків виду і довжиноюелементів є підпростір простору всіх рядків довжиноюелементів. Очевидно, що вимірність підпростору дорівнює.

3. Множина геометричних векторів, паралельних заданій площині, є підпростір простору геометричних векторів. Вимірність підпростору дорівнює 2.

Введення добутку елементів множини дозволяє визначити більш складні математичні структури, ніж лінійні простори, зокрема алгебри. Більш точно, множина елементів лінійного простору, де введено операцію множення двох елементів, яка задовольняє властивості, аналогічні властивості дійсних чисел, називають алгеброю.

Приклад.

Множина квадратних матриць однакової вимірності.

Контрольні запитання та завдання

1. Сформулюйте поняття лінійного простору.

2. Наведіть приклади лінійних просторів.

3. Сформулюйте поняття лінійної залежності елементів простору.

4. Дайте означення базису та вимірності лінійного простору.

5. В якому відношенні знаходяться базис та вимірність лінійного простору?

6. Чому дорівнює вимірність лінійного простору розв’язків однорідної системи лінійних алгебраїчних рівнянь?

7. Чому дорівнює вимірність множини геометричних векторів, паралельних даній площині?

8. Сформулюйте поняття ізоморфізму лінійних просторів.