5.3 Нормовані простори. Ортонормований базис. Процес ортогоналізації

Нормовані простори

Як кожному геометричному вектору відповідає певна довжина, що виражається додатним числом, так і кожному елементу лінійного простору можна співставити додатне число, яке відіграватиме роль довжини. Таке число, позначатимемо його, називаютьнормою елемента лінійного простору, якщо це співвідношення відповідає умовам:

1) ;

2) ;

3) .

Остання умова виражає нерівність Мінковського (1896 р.) (Minkowski H., 1864-1909, Німеччина) – нерівність трикутника.

Лінійний простір, в якому введено поняття норми, називають нормованим лінійним простором.

У кожному евклідовому просторі можна ввести норму за допомогою формули

.

Доведення.

Дійсно, така норма задовольняє всі наведені три умови. Це очевидно для першої умови, якщо під квадратним коренем розуміти арифметичний корінь, тобто додатне число. Тоді для другої умови маємо

.

Для перевірки третьої умови використаємо нерівність Коші-Буняковського

Що й потрібно було довести.

Приклади нормованих просторів.

1. Простір геометричних векторів. Норма геометричного вектора співпадає з його довжиною

.

2. Арифметичний простір елементів , в якому скалярний добуток введений за допомогою формули

.

Тоді норма буде встановлена як .

Кут між елементами нормованого евклідового простору

Знову використовуючи аналогію з геометричними векторами, визначимо кут між двома елементами танормованого евклідового простору через скалярний добуток. Тоді

.

Визначений таким чином косинус має зміст, бо величина дробу не перевищує одиниці за модулем. Дійсно, згідно з нерівністю Коші-Буняковського, чисельник менше або дорівнює знаменнику

.

Приклади введення кута між елементами евклідового простору.

1. У просторі геометричних векторів маємо тотожність

.

2. В арифметичному просторі -

.

Якщо для двох даних елементів , то такі елементи називають ортогональними. Отже, умова ортогональності двох елементів, якщо ні один з них не дорівнює нулю, має вигляд

.

Теорема. Нехай система елементів попарно ортогональна, тобто, де ; .Тоді ці елементи лінійно незалежні.

Доведення.

Доведемо від протилежного. Припустимо, що вони лінійно залежні. Отже, є такі числа (з яких хоча б одне відмінне від нуля), що

.

Помножимо цю рівність скалярно на . Маємо

,

оскільки .

Помножуючи послідовно на одержимо, що, тобто рівність можлива тільки за нульових коефіцієнтів. Відтак, елементи лінійно незалежні.

Теорему доведено.

Отже, в п-вимірному просторі п попарно ортогональних елементів можна брати як базис, який називається ортогональним базисом.

Ортонормований базис

Якщо кожний елемент ортогонального базису помножити на число, обернене його нормі, одержимо ортонормований базис

.

Елементи цього базису попарно-ортогональні, бо

,.

За нормою (при ) дорівнюють одиниці

.

За допомогою символа Кронекера ці дві умови можна записати так

Будь-який елемент евклідового простору розмірності п може бути розкладений за цим базисом

.

Як наголошувалося, скалярний добуток двох елементів, заданих у довільному базисі , за формулою (5.3) має вигляд

,

де . Якщо ж базис ортонормований, то цей вигляд значно спрощується, бо тоді, і

.

До речі, якщо норма елемента в довільному базисі записується через координати

,

то в ортонормованому базисі вона матиме значно простіший вигляд

.

Зауваження.

У просторі геометричних векторів репер є ортонормований базис. Тому скалярний добуток векторівічерез їх координати в цьому базисі запишеться так

.

Ортонормування базису

В силу його зручності завжди бажано мати ортонормований базис. Його можна побудувати на основі будь-якого базису . Це робиться за допомогою процедуриортонормування, яка полягає в наступному.

Як перший елемент нового базису візьмемо : .

За основу другого елемента візьмемо :, де єортогональним :. З цього випливає, що, тобто

.

Таким чином, маємо

За основу третього елемента візьмемо : , де є ортогональнимі:,.Беручи до уваги, що , маємо ;.

Звідки

,.

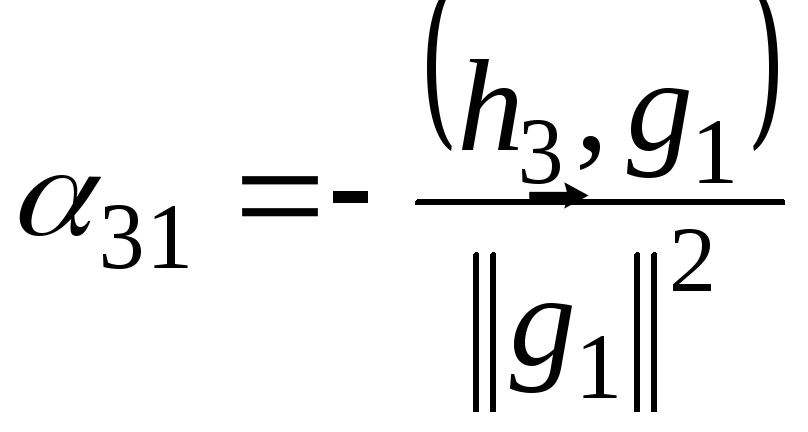Продовжуючи цей процес, одержимо всі п ортогональних елементів:

,,

де

,

причому .

Нормуючи тепер цю систему, одержимо ортонормований базис

.

Приклад.

Хай у чотиривимірному арифметичному просторі введено скалярний добуток

.

Візьмемо базис ,,,. Знайти ортонормований базис.

Розв'язання.

Ці елементи лінійно незалежні, в чому легко переконатися, якщо скласти з цих рядків матрицю і знайти її ранг. Він дорівнює чотирьом. Але ці елементи не ортогональні. Наприклад, .

Проведемо процес ортогоналізації:

; ;

;

,;

;

; .

Норми елементів дорівнюють:

, , , .

У підсумку маємо ортонормований базис:

,,,

.

У подальшому як базис використовуватимемо тільки ортонормований базис.

Проекція елемента

Важливим поняттям є проекція елемента на заданий елемент:

.

Якщо , то. Якщоспівпадає з одним із базисних елементів, то ,

Приклад.

Розглянемо проекцію вектора на вісьв просторі геометричних векторів (рис.5.8)

.

Рисунок 5.8

Звідки ,,.

Контрольні запитання та завдання

1. Дайте визначення норми елемента лінійного простору.

2. Чому дорівнює норма елемента евклідового простору? Доведіть нерівність Мінковського.

3. Як визначається кут між елементами нормованого простору?

4. Який базис називається ортонормованим?

5. Наведіть алгоритм ортонормування базису.

161