
6 Лінійні оператори. Квадратичні форми
Сучасне визначення оператора дав Дж. Пеано (Peano G., 1858-1932 рр., Італія) у 1888 р. Класифікація квадратичних форм проводиться за допомогою критерію Сільвестра (Sylvester James Joseph, 1814–1897 рр., Англія).
6.1 Лінійні оператори. Матриця оператора
Основні поняття
Нехай
задані два лінійні простори
![]() і
і![]() .
Якщо кожному елементу
.
Якщо кожному елементу![]() поставлено у відповідність певний
елемент
поставлено у відповідність певний
елемент![]() ,
то кажуть, що задано відображення
,
то кажуть, що задано відображення![]() ,
абооператор
,
абооператор
![]() ,
який здійснює це відображення:
,
який здійснює це відображення:![]() .
.
Оператор
![]() лінійний,
якщо:
лінійний,
якщо:
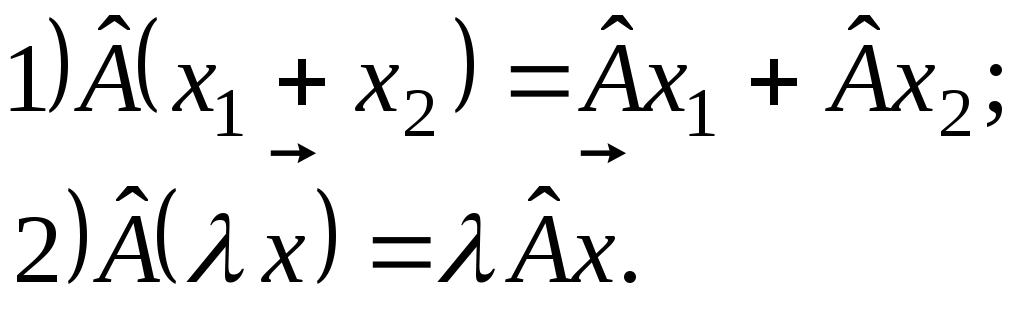
Тобто
дія оператора на суму двох елементів
рівносильна складанню результатів дії
оператора на кожний з елементів доданків,
а дія оператора на елемент, помножений
на число, рівносильна помноженню на це
число результату дії оператора на самий
елемент. До речі, з цього випливає, що
![]() .
.
Оператор не обов’язково переводить елементи одного простору в інший, він може діяти і в межах одного простору, переводячи елементи даного простору в елементи цього ж простору. В цьому разі можна виділити три специфічних оператори:
1) нульовий
оператор
![]() ;
;
2) тотожний
оператор
![]() ;
;
3)
протилежний оператор
![]() .
.
Приклади.
1![]() .
Оператор
.
Оператор![]() проектування геометричних векторів на
задану вісь
проектування геометричних векторів на
задану вісь![]() :
:![]() (рис.6.1).
(рис.6.1).
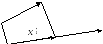
![]()
Рисунок 6.1
2. Оператор
![]() дзеркального відображення геометричних
векторів щодо заданої площини:
дзеркального відображення геометричних
векторів щодо заданої площини:![]() (рис.6.2).
(рис.6.2).
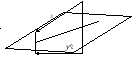
Рисунок 6.2
3. Оператор
![]() повороту геометричних векторів на кут
повороту геометричних векторів на кут![]() навколо осі0z:
навколо осі0z:
![]() (рис. 6.3).
(рис. 6.3).
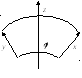
Рисунок 6.3
4. Оператор
![]() векторного добутку на вектор ліворуч
векторного добутку на вектор ліворуч![]() :
:![]() .
.
5.
Оператор
![]() диференціювання функції в просторі
функцій, які мають похідну:
диференціювання функції в просторі
функцій, які мають похідну:![]() .
.
Арифметичні дії над операторами
Над операторами можна виконувати арифметичні дії додавання, множення на число, множення оператора на оператор. При цьому одержують нові оператори.
Сума
двох операторів
![]() – це оператор, дія якого дорівнює сумі
результатів дії на кожний із доданків:
– це оператор, дія якого дорівнює сумі
результатів дії на кожний із доданків:
![]() .
.
Добуток
оператора
![]() на число
на число
![]() – це новий оператор
– це новий оператор![]() ,
який діє за правилом
,
який діє за правилом
![]() .
.
Добуток
операторів
![]() визначається так
визначається так
![]() ,
,
тобто
на елемент
![]() спочатку діє оператор
спочатку діє оператор![]() ,
а потім на результат діє оператор
,
а потім на результат діє оператор![]() .
.
Властивості арифметичних дій
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
Зауваження.
1. З
існування добутків
![]() не виходить рівність
не виходить рівність
![]() .
.
2. Якщо
![]() , то оператори називаються переставними.
, то оператори називаються переставними.
Для
операторів можна також ввести поняття
оберненого оператора, а саме, для даного
оператора
![]() існуєобернений
оператор
існуєобернений
оператор
![]() ,
якщо виконуються рівності
,
якщо виконуються рівності
![]() ,
,
де
![]() – тотожний оператор. Якщо цей оператор
– тотожний оператор. Якщо цей оператор![]() має обернений, то із співвідношення
має обернений, то із співвідношення![]() випливає
випливає![]() .
.
Не будь-який оператор має обернений. Існування оберненого оператора визначається такими теоремами.
Теорема.
Якщо оператор
![]() має обернений, то із рівності
має обернений, то із рівності![]() випливає, що
випливає, що![]() .
.
Доведення.
Дійсно,
нехай
![]() .
Тоді
.
Тоді![]() .
Оскільки
.
Оскільки![]() ,
то звідси маємо
,
то звідси маємо![]() ,
або
,
або![]() .
.
Теорему доведено.
Теорема.
Для того щоб оператор
![]() мав обернений, необхідно і достатньо,
аби оператор
мав обернений, необхідно і достатньо,
аби оператор![]() діяв із простору
діяв із простору![]() у простір
у простір![]() взаємно однозначно, тобто два різних
елементи
взаємно однозначно, тобто два різних
елементи![]() і
і![]() цей оператор відображав у два різних
елементи
цей оператор відображав у два різних
елементи![]() і
і![]() .
.
Доведення.
Необхідність.
Хай оператор має обернений, але діє не
однозначно, тобто
![]() і
і![]() .
Тоді
.
Тоді![]() ,
звідки, згідно з попередньою теоремою,
маємо
,
звідки, згідно з попередньою теоремою,
маємо
![]() або
або
![]() .
Відтак, припущення було неправильним.
.
Відтак, припущення було неправильним.
Достатність.
Хай оператор діє однозначно. Тоді кожному
елементу
![]() відповідає свій елемент
відповідає свій елемент![]() ,
такий, що
,
такий, що![]() .
Відтак, існує такий оператор
.
Відтак, існує такий оператор![]() ,
що
,
що![]() ,
або
,
або![]() ,
тобто
,
тобто![]() .
З іншого боку
.
З іншого боку![]() ,
тобто
,
тобто![]() .
Таким чином,
.
Таким чином,![]() ,
що згідно з визначенням означає, що
оператор
,
що згідно з визначенням означає, що
оператор![]() – обернений:
– обернений:![]() .
.
Теорему доведено.
Множина
елементів
![]() ,
таких, що
,
таких, що![]() ,
називаєтьсяядром
оператора і позначається як
,
називаєтьсяядром
оператора і позначається як
![]() .
Якщо
.
Якщо![]() ,
то оператор
,
то оператор![]() має обернений. Множина елементів
має обернений. Множина елементів![]() ,
таких, що
,
таких, що![]() ,
де
,
де![]() пробігає весь простір
пробігає весь простір![]() ,
називаєтьсяобластю
значень
оператора і позначається як
,
називаєтьсяобластю
значень
оператора і позначається як
![]() .
Якщо
.
Якщо![]() ,
то
,
то![]() .
.
У загальному випадку
![]() .
.
На
основі попередньої теореми можна дійти
висновку, що оператор проектування
![]() не має оберненого, а оператори дзеркального
відображення
не має оберненого, а оператори дзеркального
відображення![]() і повороту
і повороту![]() мають. Це очевидно з геометричних
образів. Але переважно виявити властивості
оператора зручніше за допомогою його
матриці.
мають. Це очевидно з геометричних
образів. Але переважно виявити властивості
оператора зручніше за допомогою його
матриці.
Матриця оператора
Виберемо
в даному лінійному просторі
![]() базис
базис![]() .
Подіємо на кожний елемент базису даним
оператором
.
Подіємо на кожний елемент базису даним
оператором![]() і результат дії розкладемо за цим же
базисом:
і результат дії розкладемо за цим же
базисом:
![]()
![]()
![]() .
.
Розташуємо
коефіцієнти
![]() у стовпці і побудуємо з них матрицю
у стовпці і побудуємо з них матрицю![]() ,
яка і називаєтьсяматрицею
оператора.
Тоді дія оператора на будь-який вектор
може бути описана таким способом
,
яка і називаєтьсяматрицею
оператора.
Тоді дія оператора на будь-який вектор
може бути описана таким способом
![]() .
.
Отже,
координати
образу
![]() легко знаходяться черезкоординати
прообразу
легко знаходяться черезкоординати
прообразу
![]() за
допомогою матриці оператора
за
допомогою матриці оператора
![]() ,
,
де
![]() і
і![]() –
матриці-стовпці з координат
–
матриці-стовпці з координат
![]() і
і
![]() .
.
Отже,
кожному оператору
![]() при вибраному базисі відповідає матриця
при вибраному базисі відповідає матриця![]() .
Справедливе і обернене. Кожній квадратній
матриці можна співставити оператор.
Дійсно
.
Справедливе і обернене. Кожній квадратній
матриці можна співставити оператор.
Дійсно
![]() .
.
Ранг матриці оператора називають рангом оператора. Він дорівнює вимірності області визначення оператора.
Приклад.
Побудувати матрицю оператора
проектування на площину
![]() .
.
Розв'язання.
Виберемо базис
![]() .
Тоді (рис.6.4):
.
Тоді (рис.6.4):![]()
![]()
![]() .
.
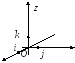
![]()
![]()
Рисунок 6.4
Звідси маємо матрицю:
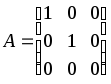 .
.
Слід звернути увагу, що як оператор, так і матриця не мають обернених.
Приклад.
Побудувати матрицю оператора
повороту навколо осі
![]() на кут
на кут![]() (рис.6.5).
(рис.6.5).


Рисунок 6.5
Розв'язання.
Через те,
що
![]()
![]()
![]() ,
маємо матрицю
,
маємо матрицю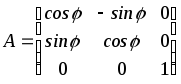 .
Як матриця, так і оператор мають обернені.
Тепер для будь-якого вектора
.
Як матриця, так і оператор мають обернені.
Тепер для будь-якого вектора
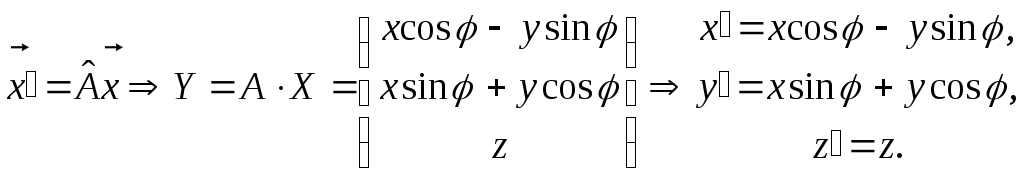
Приклад.
Хай оператор
![]() означає векторний добуток на вектор
означає векторний добуток на вектор![]() зліва:
зліва:![]() .
Знайти його матрицю.
.
Знайти його матрицю.
Розв'язання.
Дія оператора на базисні
вектори:
![]()
![]()
![]() .
.
Матриця оператора має вигляд
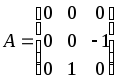 .
.
Приклад.
Хай оператор диференціювання
діє у лінійному просторі многочленів
степені не вище
![]() .
Знайти його матрицю в базисі
.
Знайти його матрицю в базисі![]() .
.
Розв'язання.
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() .
.
Матриця оператора дорівнює
 .
.
В останніх двох прикладах як матриці, так і відповідні оператори не мають обернених.
Матриця оператора в новому базисі
Із
визначення матриці оператора випливає,
що величина її елементів залежить від
базису і змінюватиметься при переході
до нового базису. Знайдемо формули
переходу. Хай оператор
![]() в базисі
в базисі![]() має матрицю
має матрицю![]() ,
а в базисі
,
а в базисі![]() –
матрицю
–
матрицю
![]() .
Це означає, що
.
Це означає, що![]() ,
,![]() .
.
Нехай
![]() –
матриця переходу від одного базису до
іншого, тобто
–
матриця переходу від одного базису до
іншого, тобто
![]() .
Тоді можна записати
.
Тоді можна записати
![]() . (6.1)
. (6.1)
Цю ж дію можна записати інакше
![]()
![]() (6.2)
(6.2)
Прирівнюючи розкладення в (6.1) і (6.2), одержимо
![]() ,
,
або в матричному запису
![]() .
.
Таким чином, матриця оператора в новому базисі пов’язана з матрицею в старому базисі формулою
![]() .
(6.3)
.
(6.3)
Використовуючи
властивість матриць
![]() ,
легко довести, щовизначник
матриці оператора при переході до нового
базису не змінюється.
Дійсно з (6.3) маємо:
,
легко довести, щовизначник
матриці оператора при переході до нового
базису не змінюється.
Дійсно з (6.3) маємо:
![]() ,
де взято до уваги, що
,
де взято до уваги, що![]() .
.
Контрольні завдання
1. Дайте визначення лінійного оператора.
2. Наведіть приклади лінійних операторів.
3. Сформулюйте правила арифметичних дій над операторами.
4. Сформулюйте теорему про існування оберненого оператора.
5. Дайте алгоритм побудови матриці оператора.
6. Виведіть формулу перетворення матриці оператора при переході до нового базису.
