2.4 Дії над векторами, які задані проекціями (координатами))

Нехай вектори й задані своїми проекціями на осі координат Ox, Оу, Oz або в базисі розкладені по ортах координатних осей

,.

Лінійні операції над векторами

Лінійні операції над векторами зводяться до відповідних лінійних операцій над проекціями цих векторів:

1) при додаванні (відніманні) векторів їхні однойменні координати складаються (віднімаються)

або

;

2) при множенні вектора на скаляр координати вектора множаться на цей скаляр

або .

Рівність векторів

З означення вектора як спрямованого відрізка, який можна пересувати в просторі паралельно самому собі, виходить, що два вектори і рівні тоді й тільки тоді, коли виконуються рівності: , тобто

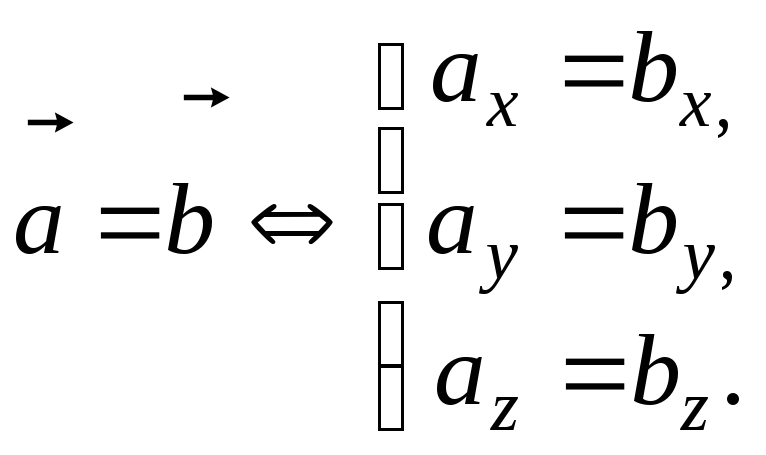
Колінеарність векторів

З'ясуємо умови колінеарності векторів і , які задані своїми координатами.

Відомо, що ненульові вектори йколінеарні тоді й тільки тоді, колиабо,де – деяке число. Це рівносильно виконанню рівності . Звідси , , , тобто або

Таким чином, проекції колінеарних векторів пропорційні. Правильним є й зворотне твердження: вектори, що мають пропорційні координати, колінеарні.

Радіус-вектор точки

Нехай у просторі задана декартова прямокутна система координат Oxyz. Вектор називається радіус-вектором точки й позначається , тобто . Оскільки координати вектора збігаютьсяз координатами точки , то розкладання по ортах має вигляд

Координати радіус-вектора записуються у вигляді.

Координати вектора

Знайдемо координати вектора , якщо відомі координати точок A(;;) і В(;;). Маємо (рис. 2.12)

Рисунок 2.12

Отже, координати вектора дорівнюють різницям відповідних координат його кінця та початку: =.

Відстань між точками A і В або довжина вектора визначається за формулою

.

Поділ відрізка в даному відношенні

Нехай точка М ділить відрізок АВ у відношенні . Тоді(рис. 2.13).

Рисунок 2.13

Нехай задані точки й .Координати точки обчислюються за формулами

, ,, (2.7)

які називаються формулами поділу відрізка в даному відношенні.

Доведення.

Через те, що , , а вектор , то, враховуючи, що рівні вектори мають рівні координати, маємо

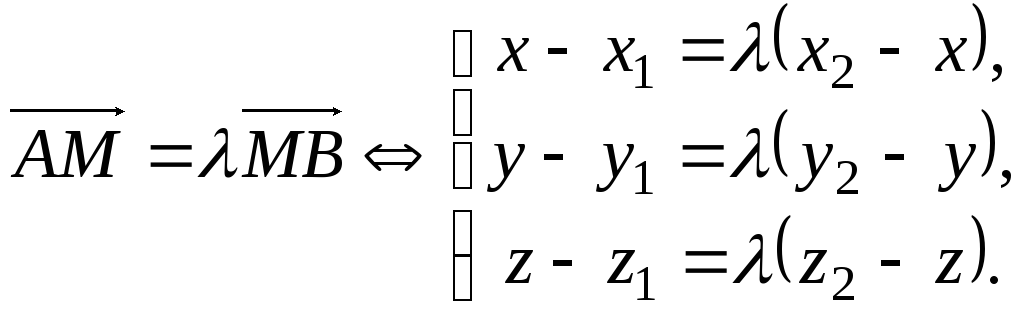
Звідки

, ,.

Зокрема, при =1, тобто якщо, формули (2.7) приймуть вигляд

, ,.

У цьому випадку точка є серединою відрізка АВ.

Зауваження.

1. Якщо , то це означає, щоточки А і М збігаються.

2. Якщо < 0, тоточка М лежить поза відрізком АВ – говорять, що точка М ділить відрізок АВ зовнішнім чином.

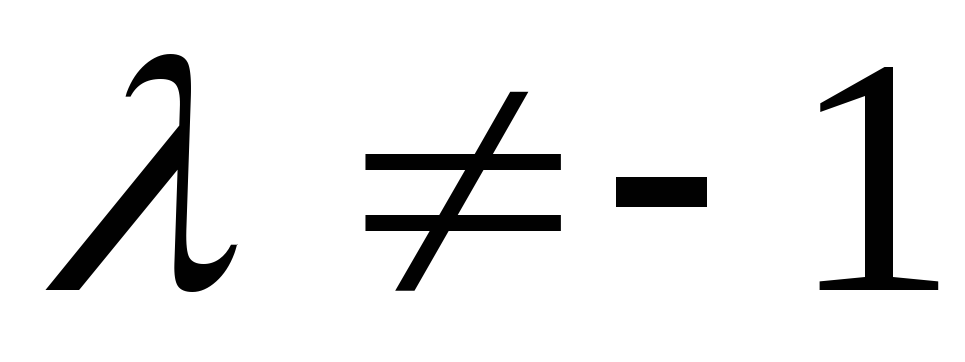3. , тому що в протилежному випадку 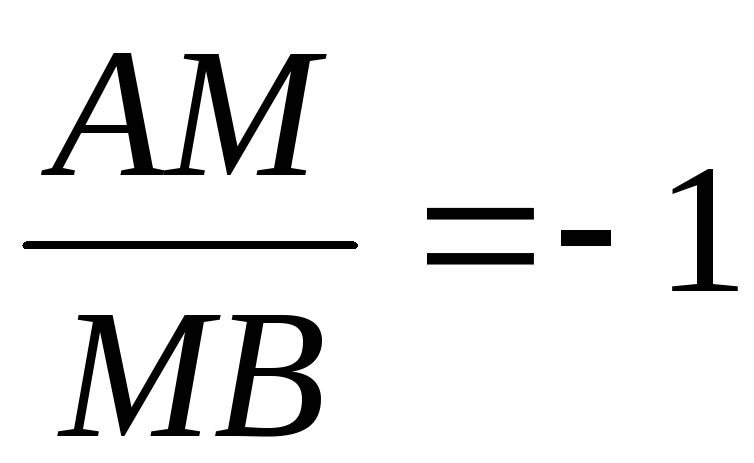,AM+MB=0 .

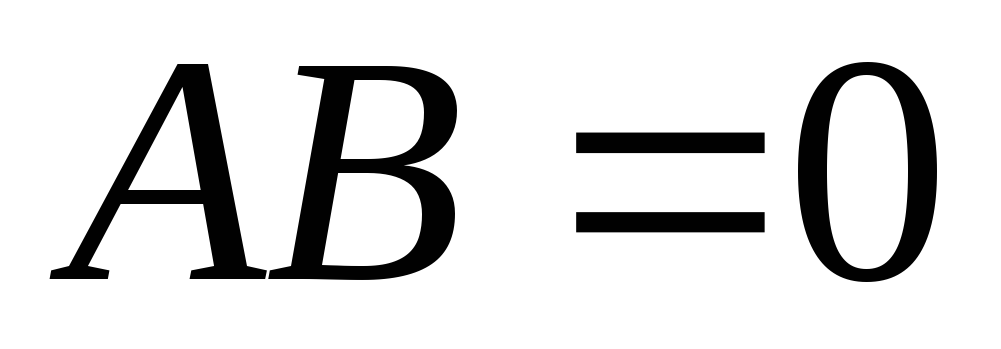Приклад .

Знайти координати одиничного вектора, який є направленим за бісектрисою кута, утвореного векторами і.

Розв'язання.

Знайдемо орти векторів і :,.Через те, що , то вектор, який є сумою векторів і, тобто вектор, спрямований по діагоналі ромба, побудованого на векторахі. Якщо поділити векторна його довжину, то отримаємо шуканий одиничний вектор:

; ;

; ;

;

;

.

Приклад .

Заданий трикутник з вершинами .Знайти:

1. координати орта ;

2. ;

3. ;

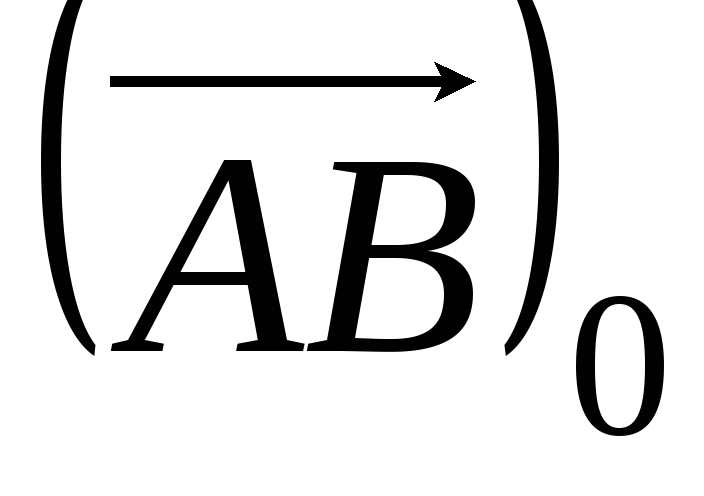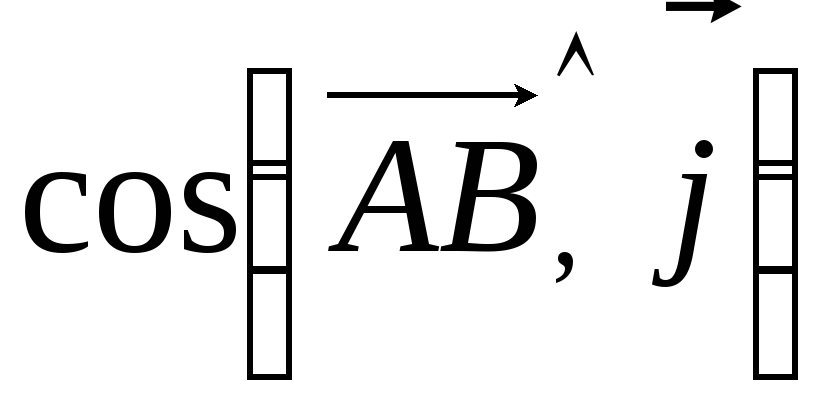4. координати точки перетину бісектриси кута А зі стороною .

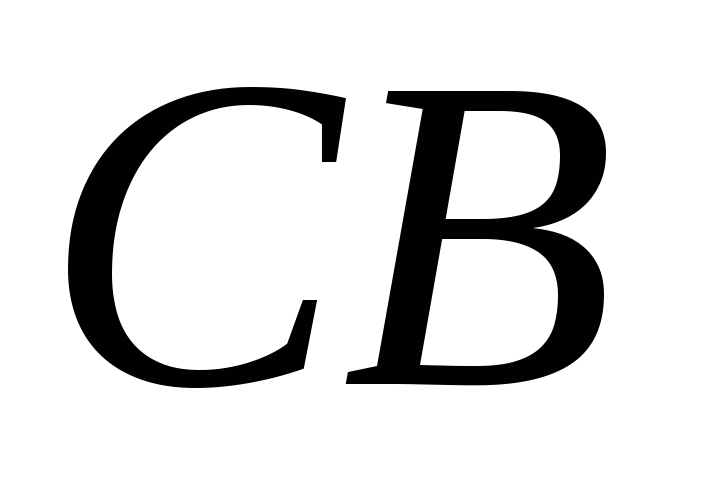Розв'язання.

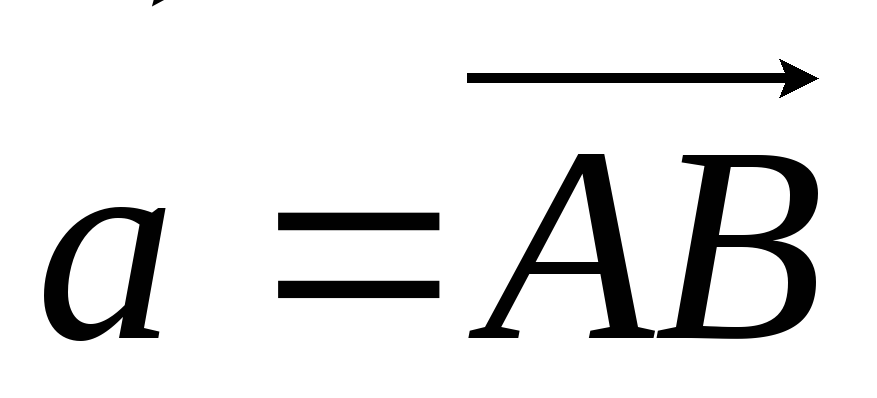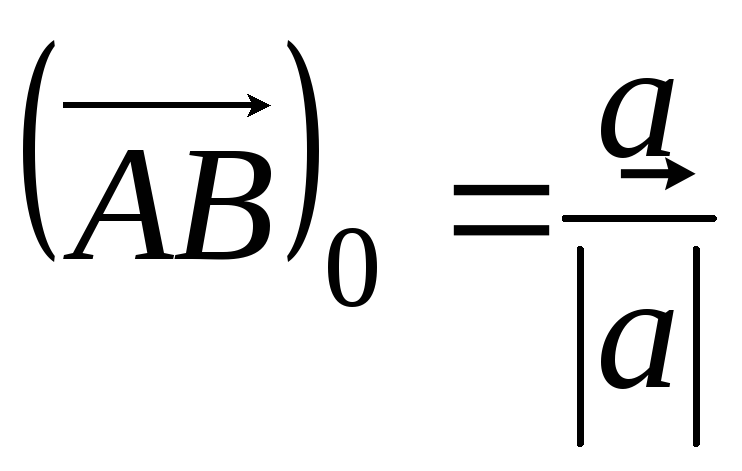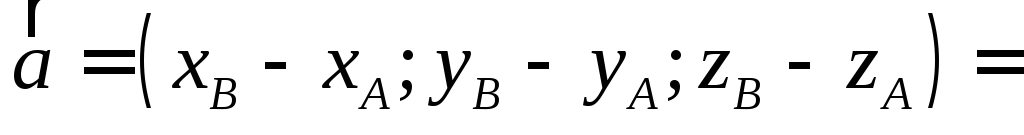
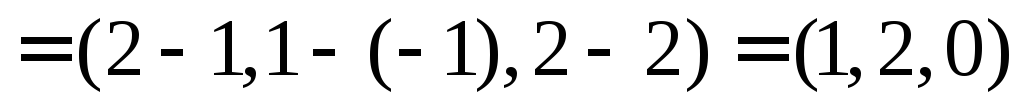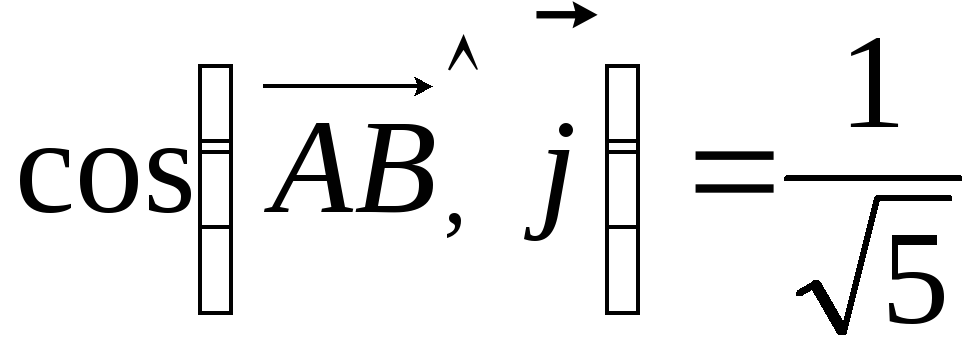
1. Позначимо . Через те, що, де , , то координати орта ;

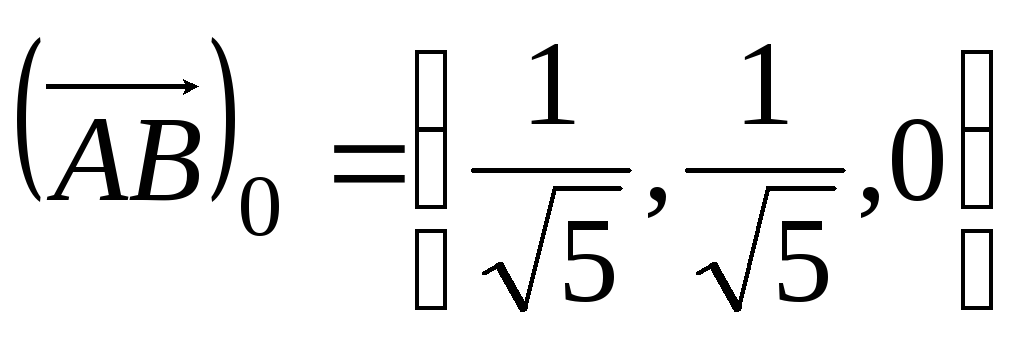2. Напрямний косинус вектора на базисний вектордорівнює координаті орта 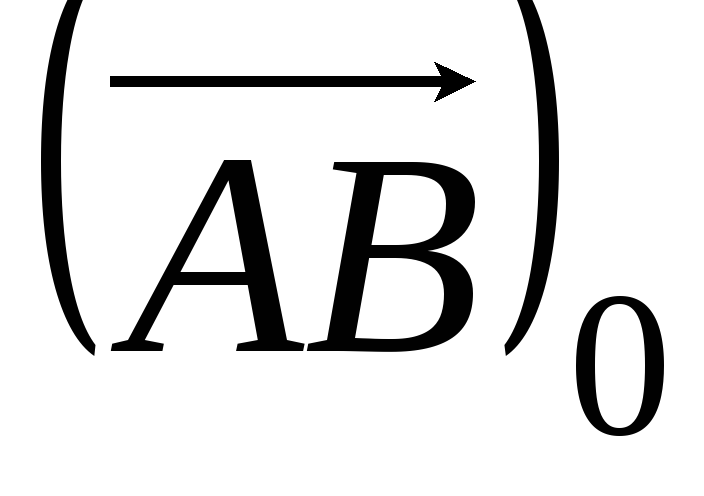на ось: ;

3. Проекція вектора на базисний вектордорівнює координаті цього вектора на вісь: ;

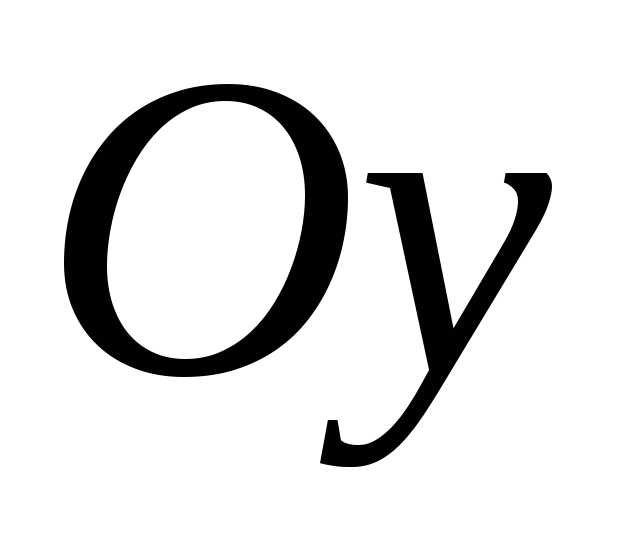4. Знайдемо довжину сторін трикутника 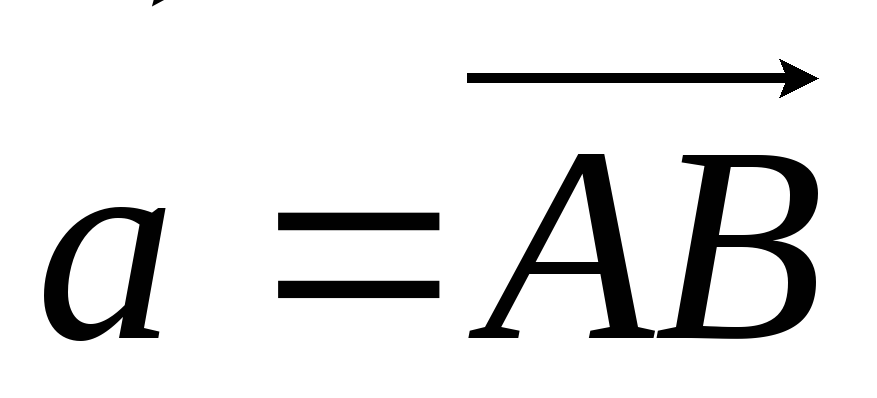, , 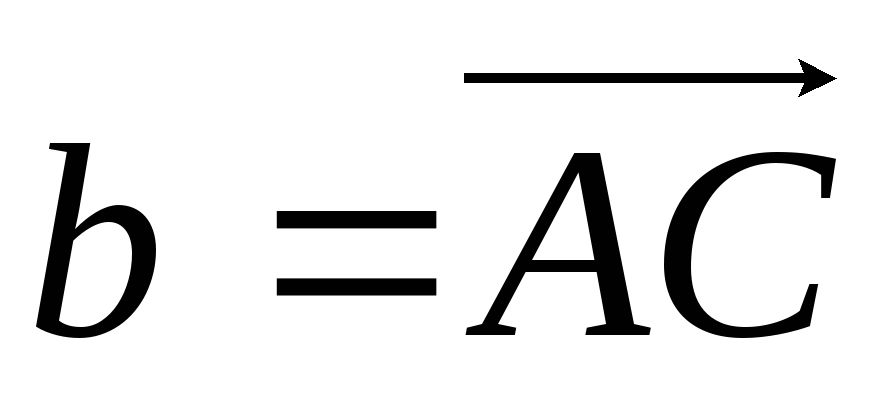які утворюють кут А:

, ;

, .

Через те, що бісектриса кута А ділить сторону на частини, що пропорційні прилеглим сторонам, то. Отже,

, ,

,

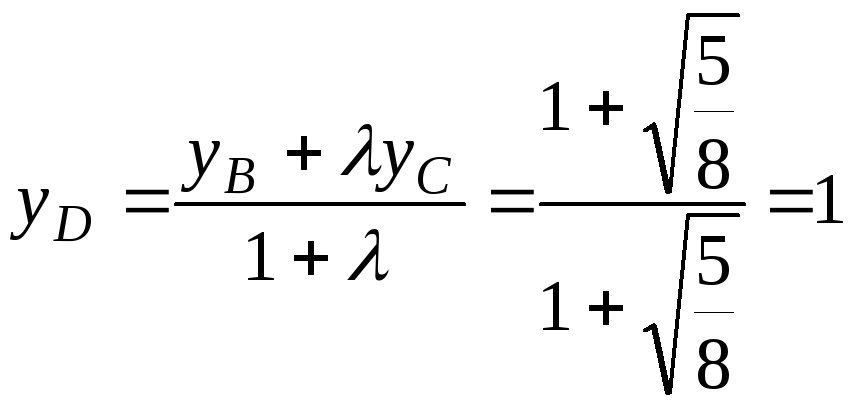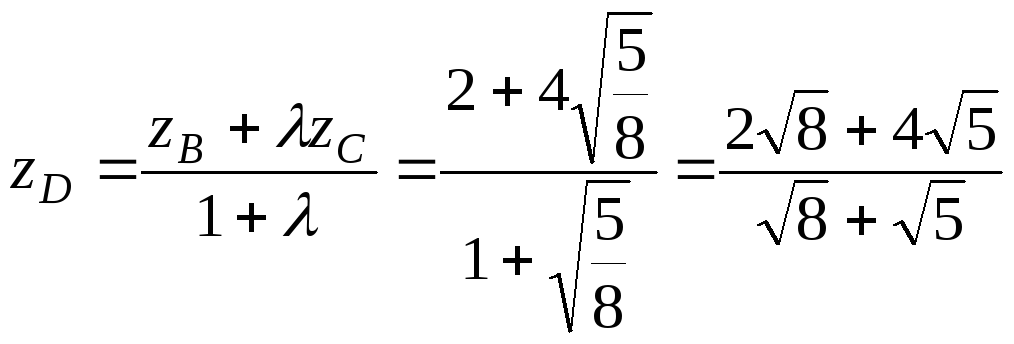шукана точка .

Контрольні запитання

1. Чому дорівнюють координати вектора ;, якщо

, ?

2. Як визначається рівність векторів, що задані своїми координатами?

3. Як визначається колінеарність векторів, що задані своїми координатами?

4. Що називається радіус-вектором точки ?

5. Якщо відомі координати точок A(;;) і В(;;), то чому дорівнюють координати вектора ?

6. Що означає розділити відрізок у відношенні ?

7. Чому дорівнюють координати точки , що ділитьвідрізок АВ у відношенні , якщо заданіточки й ?