2.2 Проекція вектора на вісь

Основні поняття

Н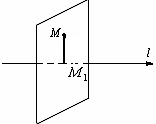ехай у просторі задана вісьl, тобто спрямована пряма. Проекцією точки М на вісь l називається основа перпендикуляра, опущеного із точки на вісь.

Точка єточкою перетину осі l із площиною, що проходить через точку М перпендикулярно осі.

Якщо точка М лежить на осі , то проекція точки М на вісь збігається з М.

Нехай – довільний вектор (). Позначимо черезіпроекції на вісь відповідно до початку А і кінця В вектора й розглянемо вектор (рис. 2.7).

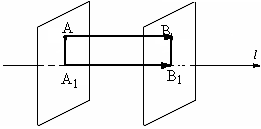
Рисунок 2.7

Проекцією вектора на вісь називається додатне число, якщо векторі вісьl однаково спрямовані й від'ємне число , якщо вектор і вісь l протилежно спрямовані. Якщо точки й збігаються (=0), то проекція векторадорівнює 0.

Проекція вектора на вісь позначається так: . Таким чином, із означення маємо

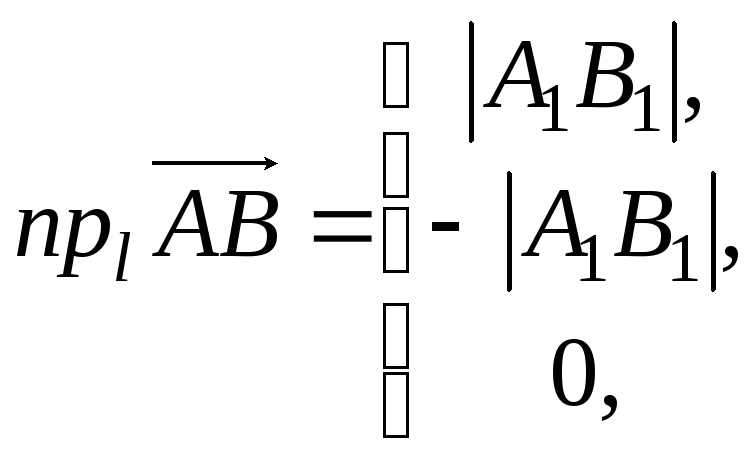
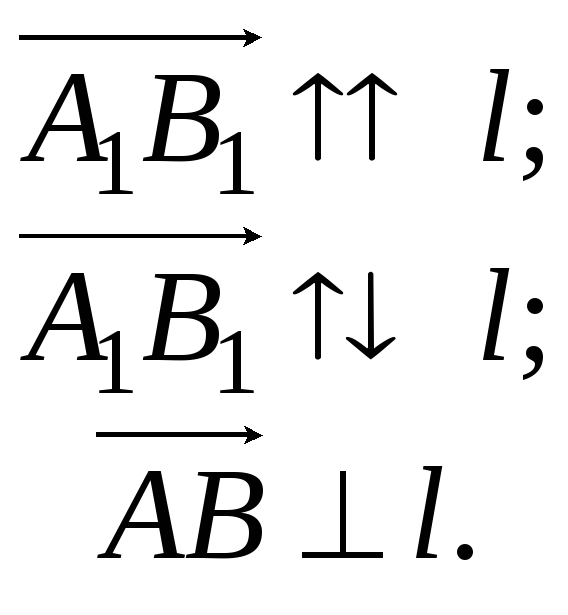
Кут між векторомі віссю l (або кут між двома векторами) зображений на рис. 2.8. Очевидно, що .

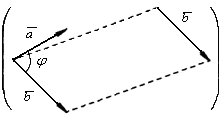
Рисунок 2.8

Властивості проекцій

1. Проекція вектора на вісь дорівнює добутку модуля вектора на косинус кутаміж вектором та віссю, тобто

.

Доведення.

Якщо , то .

Якщо , то .

Якщо , то.

Наслідки.

1. Проекція вектора на вісь додатна (від'ємна), якщо вектор утворює з віссю гострий (тупий) кут, і дорівнює нулю, якщо цей кут – прямий.

2. Проекції рівних векторів на ту саму вісь рівні між собою.

2. Проекція суми декількох векторів на ту саму вісь дорівнює сумі їхніх проекцій на цю вісь, тобто

.

Доведення.

Н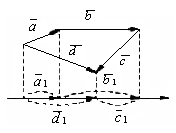ехай, наприклад,. Маємо

, тобто .

3. При множенні вектора на число його проекція на вісь також помножується на це число, тобто

.

Доведення.

При : .

При : .

При властивість очевидна.

Таким чином, лінійні операції над векторами приводять до відповідних лінійних операцій над проекціями цих векторів.

Базис на площині та у просторі. Розкладання вектора за базисом

Базисом на прямій називається всякий ненульовий вектор цієї прямої. Будь-які два неколінеарних вектори , взяті у певному порядку, утворять базис на площині. Базисом у просторі назвемо три некомпланарних вектори, взятих у певному порядку.

Теорема. Будь-який вектор на площині може бути єдиним способом розкладений по базисних векторах , тобто .

Доведення.

Перший випадок. Нехай ||. Тоді з необхідної та достатньої умови колінеарності двох векторів маємо . Отже,

Другий випадок. Нехай вектор не є колінеарним ні вектору , ні вектору (рис. 2.9).

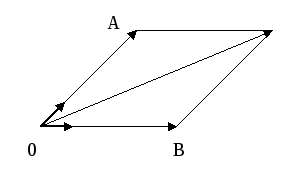
Рисунок 2.9

Тоді , де||, а ||. Через те, що і, то.

Теорему доведено.

Коефіцієнти в розкладанні називаютьсякоординатами вектора в базисі.

Теорема. Будь-який вектор у просторі може бути єдиним способом, розкладений по базисних векторах ,тобто .

Доведення.

З деякої точки О відкладемо всі чотири вектори: й . Через точкуА проведемо три площини, які паралельні відповідним площинам, що проведені через пари векторів ; ; .Точки перетину зазначених площин із прямими, на яких лежать вектори ,позначимо відповідно через . Проводячи такі побудови, одержимо паралелепіпед, у якого– діагональ.

За означенням суми трьох векторів .Через те, що ||, ||, ||, то маємо .

Теорему доведено.

Коефіцієнти в розкладанні називаються координатами вектора в базисі.

Базис називається ортонормованим, якщо базисні вектори попарно ортогональні та довжина кожного з них дорівнює одиниці.

Контрольні запитання

1. Що називається проекцією точки; вектора на вісь?

2. Чому дорівнює значення проекції?

3. Якими властивостями володіє проекція вектора на вісь?

4. Що називається базисом на площині; у просторі?

5. Як здійснюється розкладання вектора по базисних векторах на площині; у просторі?

6. Який базис називається ортонормованим?