2.3 Розкладання вектора по ортах координатних осей. Модуль вектора. Напрямні косинуси

Основні поняття

Основою описання геометричних об’єктів за допомогою чисел є система координат, яка дозволяє поставити у відповідність кожній точці простору рядок з трьох чисел. Першій симетрії відповідає декартова прямокутна система координат, яка складається з трьох взаємно перпендикулярних прямих із заданими напрямками осей, які перетинаються в одній точці О, що називається початком системи координат (рис.2.10).

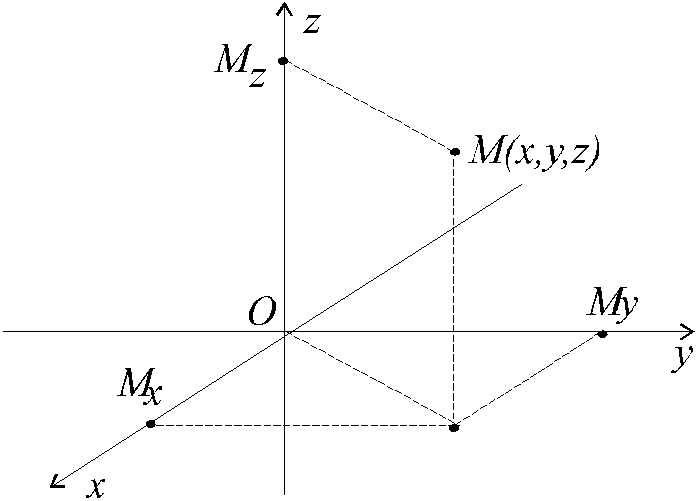
Рисунок 2.10

Розглянемо в просторі прямокутну систему координат Oxyz. Осі називають: Ox – вісь абсцис, Оу – вісь ординат, Oz – вісь аплікат. Кожна вісь є числовою, якщо на ній виставлено масштаб. Перпендикуляр, опущений з довільної точки на кожну вісь, дає проекцію цієї точки на дану вісь:. Оскільки із цієї точки на дану пряму можна опустити тільки один перпендикуляр, то кожній точцівідповідає лише один набір точок, і навпаки. Кожній проекції на відповідній числовій осі відповідає одне число, відтак між точкою просторуі трійкою чисел встановлюється взаємно однозначна відповідність:. Числа називаються координатами точки в даній системі координат та позначаються . Трійка чисел вказує на тривимірність простору.

Якщо розглядаються об’єкти на площині, то на ній можна ввести систему координат з двох осей. Тоді точку на площині описуватиме рядок із двох чисел – . Це буде двомірний простір.

Узагальнюючи, можна вести п-вимірний простір, кожна точка якого задається рядком з п чисел: .

Розкладання вектора по ортах координатних осей

Виділимо на координатних осях Ox, Оу й Oz одиничні вектори (орти), які позначимо відповідно (рис. 2.11).

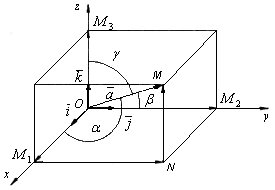
Рисунок 2.11

Виберемо довільний вектор простору й з'єднаємо його початокз початком координат: .

Знайдемо проекції вектора на координатні осі. Проведемо через кінець вектора площини, паралельні координатним площинам. Точки перетину цих площин з осями позначимо відповідно через ,і. Одержимо прямокутний паралелепіпед, однією з діагоналей якого є вектор . Тоді , ,. За означенням суми декількох векторів знаходимо . А, оскільки, ,, то

, (2.2)

де

, ,. (2.3)

Позначимо проекції вектора на осі Ох, Оу й Oz відповідно через і , тобто ,,. Тоді з рівностей (2.2) і (2.3) одержуємо

_. (2.4)

Ця формула є основною у векторному численні й називається розкладанням вектора по ортах координатних осей. Числа називаються координатами вектора , тобто координати вектора є його проекції на відповідні координатні осі.

Векторну рівність (2.4) часто записують у символічному вигляді: .

Модуль вектора

Знаючи проекції вектора , можна легко знайти вираз для модуля вектора.

На підставі теореми про довжину діагоналі прямокутного паралелепіпеда можна написати: , тобто

(2.5)

Звідси

тобто модуль вектора дорівнює квадратному кореню із суми квадратів його проекцій на осі координат.

Напрямні косинуси

Нехай кути вектора з осями Ох, Оу і Oz відповідно дорівнюють , ,. За властивістю проекції вектора на вісь, маємо

, ,. (2.6)

Або, що те саме,

cos=, cos= , cos=.

Числа cos, cos, cosназиваютьсянапрямними косинусами вектора . Підставимо вираз (2.6) у рівність (2.5), тоді маємо

,

а, якщо скоротити на , то

,

тобто сума квадратів напрямних косинусів ненульового вектора дорівнює одиниці.

Легко помітити, що координатами одиничного вектора (орта) є числа cos , cos , cos , тобто .

Отже, якщо задати координати вектора, то завжди можна визначити його модуль і напрямок, тобто сам вектор.

Приклад .

Знайти орт вектора та його напрямні косинуси.

Розв'язання.

Відомо, що орт вектора визначається як, де –довжина вектора. Через те, що , то . Оскільки напрямні косинуси, які визначаються за формулами cos=, cos= , cos= та дорівнюють координатам орта, то cos,, .

Контрольні запитання

1. Що називається декартовою прямокутною системою координат у просторі; на площині?

2. Що називається координатами точки в просторі; на площині?

3.За якою формулою здійснюється розкладання вектора по ортах координатних осей?

4. Чому дорівнює модуль вектора в просторі; на площині?

5. Що називається напрямними косинусами вектора?

6. Чому дорівнює сума квадратів напрямних косинусів ненульового вектора?